Communication Research: Building Recommendation System

스마트 TV앱의 사용자: a, b, c, d, e, f, g, i
영화에 대한 평: ManOfSteel, TheConjouring, WeAreWhat, TheUsOfLeland, TheWayBack, MonsterUniv
가정: 사용자 i가 접속하여 영화를 검색하고 있고, 이 사용자와 관련이 있는 영화를 추천하려고 함.

아래는 사용자가 영화에 대한 평을 한 것을 정리한 데이터
i가 보지 않은 영화는 ManOfSteel, WeAreWhat, MonsterUniv 인데, 이 중에서 어떤 영화가 가장 i가 좋은 평가를 할 것 같은 영화인가?

	ManOfSteel	TheConjouring	WeAreWhat	TheUsOfLeland	TheWayBack	MonsterUniv
a	5	7	6	7	5	8
b	6	7	3	10	7	6
c	5	6		7		8
d		5	6	8	4	8
e	8	7	3	6	4	5
f	6	8		10	7	6
i		9		8	2

데이터 분석을 위해서 원래 데이터를 transpose (치환) 함 (실제 programming implementation에서는 불필요할 수도 있음).

	a	b	c	d	e	f	i
ManOfSteel	5	6	5		8	6
TheConjouring	7	7	6	5	7	8	9
WeAreWhat	6	3		6	3
TheUsOfLeland	7	10	7	8	6	10	8
TheWayBack	5	7		4	4	7	2
MonsterUniv	8	6	8	8	5	6

상관관계표

	a	b	c	d	e	f	i
a	1	0.219	0.923	0.784	0	0.245	0.991
b	0.219	1	0.205	0.245	0.45	.964**	0.381
c	0.923	0.205	1	0.866	-1.000**	0.135	-1.000**
d	0.784	0.245	0.866	1	0.177	0.213	0.592
e	0	0.45	-1.000**	0.177	1	0	0.98
f	0.245	.964**	0.135	0.213	0	1	0.663
i	0.991	0.381	-1.000**	0.592	0.98	0.663	1

사용자 i와 다른 사용자들과의 상관관계표 --> i와 얼마나 같이 가는가?를 보여주는 지표

i
a	0.991
b	0.381
d	0.592
e	0.98
f	0.663

다른 사용자들이 평가한 i가 관람하지 않은 영화에 대한 평

	I	ManOfSteel	WeAreWhat	MonsterUniv
a	0.991
b	0.381
d	0.592
e	0.98
f	0.663

r * e(valuation) = 상관관계계수 * 평가값

	I	ManOfSteel	r * e	WeAreWhat	r * e	MonsterUniv	r * e
a	0.991	5	4.955	6	5.946	8	7.928
b	0.381	6	2.286	3	1.143	6	2.286
d	0.592			6	3.552	8	4.736
e	0.98	8	7.84	3	2.94	5	4.9
f	0.663	6	3.978			6	3.978

Sum(r*e) --> 이 값을 사용할 수도 있음. 그러나, 이 값은 평가를 많이 받지 못한 영화의 점수가 낮아지는 단점이 있음.
따라서, Sum(r)값을 구해 봄 (평가된 영화에 해당하는 r값을 더한 값)
Sum/rSum --> 이 값을 추천에 사용!
혹은 Sum/Count(e) 값을 사용할 수도 있음. (Count(e) = evaluation된 숫자)
혹은 . . . .

	I	ManOfSteel		WeAreWhat		MonsterUniv
a	0.991	5	4.955	6	5.946	8	7.928
b	0.381	6	2.286	3	1.143	6	2.286
d	0.592			6	3.552	8	4.736
e	0.98	8	7.84	3	2.94	5	4.9
f	0.663	6	3.978			6	3.978
	Sum(r*e)		19.059		13.581		23.828
	Sum(r)		3.015		2.944		3.607
	Sum(r*e)/Sum(r)		6.321393035		4.613111413		6.606043804
	Sum/Count(e)		4.76475		3.39525		4.7656

Sum/Sum(1-r) 를 이용.
논리: i와 상관관계가 높은 사람의 점수에 무게를 주기 위해서 (1-r) 값을 사용함. i와 상관관계가 많은 사람이 있을 수록 분모의 값이 작아지도록 함.

	r	1-r	ManOfSteel		WeAreWhat		MonsterUniv
a	0.991	0.009	5	4.955	6	5.946	8	7.928
b	0.381	0.619	6	2.286	3	1.143	6	2.286
d	0.592	0.408			6	3.552	8	4.736
e	0.98	0.02	8	7.84	3	2.94	5	4.9
f	0.663	0.337	6	3.978			6	3.978
	Sum(r*e)			19.059		13.581		23.828
	Sum(r)			3.015		2.944		3.607
	Sum(r*e)/Sum(r)			6.321393035		4.613111413		6.606043804
	Sum(1-r)			0.985		1.056		1.393
	Sum/Sum(1-r)			19.34923858		12.86079545		17.10552764

Python ¶

install python 2.xx

# A dictionary of movie critics and their ratings of a small
# set of movies
critics={
'a': 
	{'ManOfSteel': 5, 
	'TheConjouring': 7,
	'WeAreWhat': 6, 
	'TheUsOfLeland': 7, 
	'TheWayBack': 5, 
	'MonsterUniv': 8},
'b': 
	{'ManOfSteel': 6, 
	'TheConjouring': 7,
	'WeAreWhat': 3, 
	'TheUsOfLeland': 10, 
	'TheWayBack': 7, 
	'MonsterUniv': 6},
'c': 
	{'ManOfSteel': 5, 
	'TheConjouring': 6,
	'TheUsOfLeland': 7, 
	'MonsterUniv': 8},
'd': 
	{
	'TheConjouring': 5,
	'WeAreWhat': 6, 
	'TheUsOfLeland': 8, 
	'TheWayBack': 4, 
	'MonsterUniv': 8},
'e': 
	{'ManOfSteel': 8, 
	'TheConjouring': 7,
	'WeAreWhat': 3, 
	'TheUsOfLeland': 6, 
	'TheWayBack': 4, 
	'MonsterUniv': 5},
'f': 
	{'ManOfSteel': 6, 
	'TheConjouring': 8,
	'TheUsOfLeland': 10, 
	'TheWayBack': 7, 
	'MonsterUniv': 6},
'i': 
	{
	'TheConjouring': 9,
	'TheUsOfLeland': 8, 
	'TheWayBack': 2},
}

C:\Users\Hyo\CloudStation\Classes\2013-fall\DBNM\Rec py
Python 2.4.1 (#65, Mar 30 2005, 09:13:57) [MSC v.1310 32 bit (Intel)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> from recommendations import critics
>>> critics['a']['WeAreWhat']
6
>>> critics['i']['TheConjouring']=9
>>> critics['i']
{'TheWayBack': 2, 'TheConjouring': 9, 'TheUsOfLeland': 8}
>>>

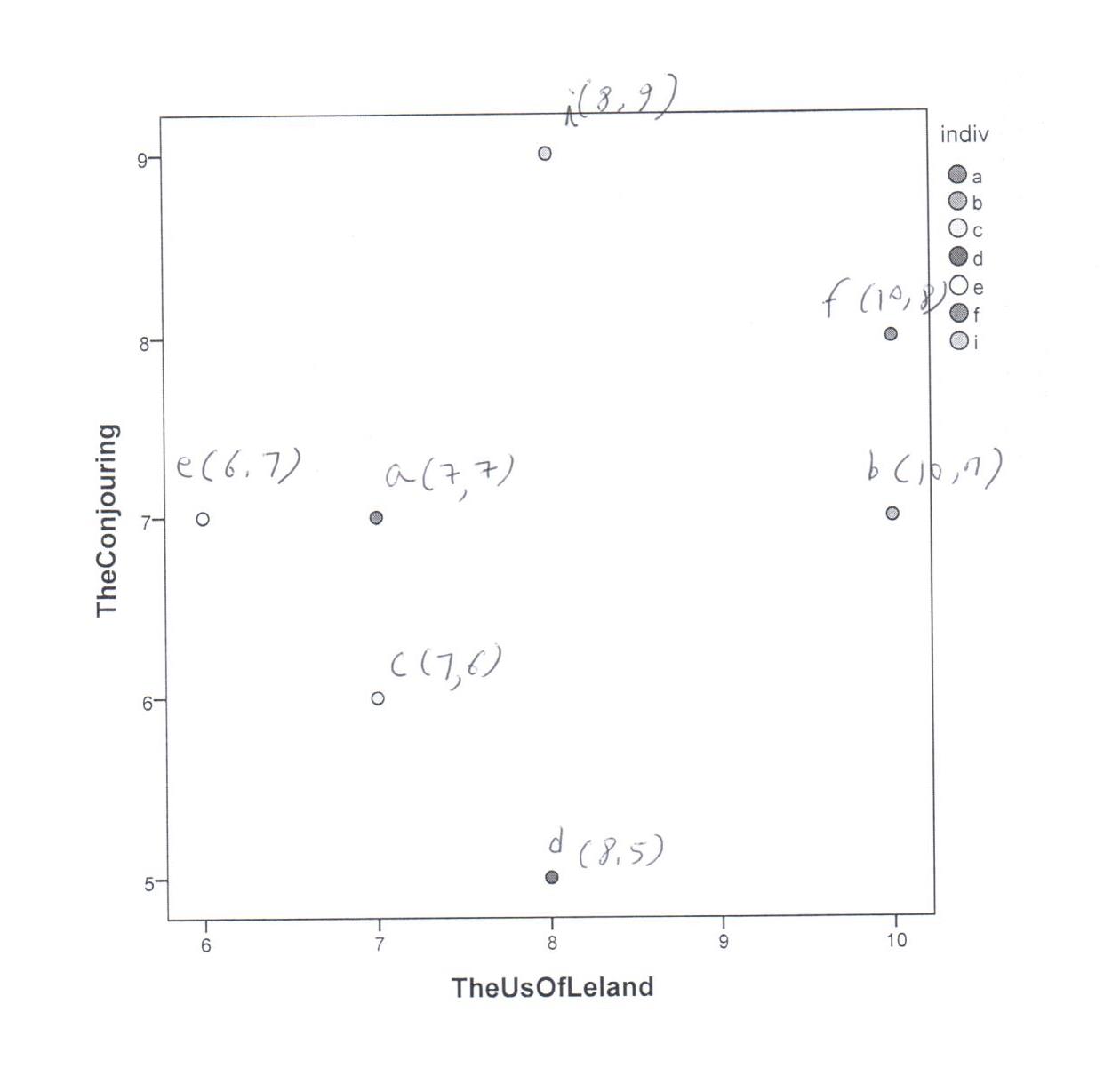
[JPG image (47.47 KB)]

i~a
i~e
i~f

>>> from math import sqrt
>>> sqrt(pow(8-7,2)+pow(9-7,2))
2.23606797749979

>>> sqrt(pow(8-6,2)+pow(9-7,2))
2.8284271247461903

>>> 1/(1+sqrt(pow(8-7,2)+pow(9-7,2)))
0.3090169943749474

from math import sqrt

# Returns a distance-based similarity score for person1 and person2
def sim_distance(prefs,person1,person2):
  # Get the list of shared_items
  si={}
  for item in prefs[person1]: 
    if item in prefs[person2]: si[item]=1

  # if they have no ratings in common, return 0
  if len(si)==0: return 0

  # Add up the squares of all the differences
  sum_of_squares=sum([pow(prefs[person1][item]-prefs[person2][item],2) 
                      for item in prefs[person1] if item in prefs[person2]])

  return 1/(1+sum_of_squares)

>>> reload(rec2)
>>> print rec2.sim_pearson(rec2.critics,'a','i')

>> reload(rec2)
>> rec2.topMatches(rec2.critics,'i',n=3)