1. CLT ¶
- Central Limit Theorem (CLT) 이란
- 평균이
 , 그리고 표준편차(
, 그리고 표준편차(  )가
)가 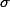 인 모든 종류의 모집단에서, 샘플 숫자를
인 모든 종류의 모집단에서, 샘플 숫자를 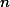 으로 하여 샘플평균을 분포시키면, 그 분포는 정규분포(normal distribution)에 가까와지며, 그 분포의 평균(mean,
으로 하여 샘플평균을 분포시키면, 그 분포는 정규분포(normal distribution)에 가까와지며, 그 분포의 평균(mean, 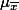 )은
)은  와 같은 값이 되고, 표준편차(stdev,
와 같은 값이 되고, 표준편차(stdev, 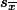 )는
)는 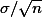 가 된다는 것이다.
가 된다는 것이다.
- sample을 취하는 population이 normal distribution을 이룬다
- n이 비교적 클 때. 약 30 이상일 때.
위의 문장이 의미하는 것은 수 많은 샘플을 취했을 때, 그 샘플들의 평균은 실제 population의 평균값에 근사하게 된다는 것을 의미한다. (위의 이유에서, the mean of the distribution of sample means를 expected value of  라고 부른다.)
라고 부른다.)
 라고 부른다.)
라고 부른다.) Standard error:: standard deviation of the distribution of sample means를 특별히 standard error of  라고 부른다.
라고 부른다.
 라고 부른다.
라고 부른다. Standard error 또한 standard deviation 이므로 (즉, standard deviation of distribution of sample means), 각 샘플의 평균이 샘플들의 평균값(the mean of distribution of sample means)에서 얼마나 떨어져 있는 가를 나타내는 지표로 쓰인다. 다시 말하면, 이 특별한 standard deviation은 내가 샘플링을 했을 때, 그 샘플의 평균값이 population mean에서 얼마나 떨어져 있을 수 있는가의 가능성(확율)을 나타내는 값이다. 즉, standard error = 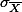 = standard deviation distance between
= standard deviation distance between  and
and  라고 할 수 있다. 이 standard error 값에 영향을 주는 것은 두 가지가 있다.
라고 할 수 있다. 이 standard error 값에 영향을 주는 것은 두 가지가 있다.
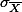 = standard deviation distance between
= standard deviation distance between  and
and  라고 할 수 있다. 이 standard error 값에 영향을 주는 것은 두 가지가 있다.
라고 할 수 있다. 이 standard error 값에 영향을 주는 것은 두 가지가 있다. Standard error의 공식을 다시 써보면 아래와 같은데,
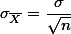
- 샘플의 크기 (n)
- population의 standard deviation 가 있다.
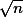 의 값은 커지고, 따라서 se의 값은 작아진다는 것을 의미한다. se가 작아진다는 것은 distribution of samples means 의 전체적인 분포곡선이 평균을 중심으로 좁게 분포되어 있다는 것을 의미하고, 이는 곧 n값이 크게 되면, 한 샘플의 평균이 원래 평균에서 크게 벗어나지 않게 된다는 것을 의미한다. 우리가 샘플의 크기를 적당히 크게 잡는 이유는 한 샘플의 평균이 원래의 모집단 평균에서 크게 벗어나지 않기를 바라기 때문이다.
의 값은 커지고, 따라서 se의 값은 작아진다는 것을 의미한다. se가 작아진다는 것은 distribution of samples means 의 전체적인 분포곡선이 평균을 중심으로 좁게 분포되어 있다는 것을 의미하고, 이는 곧 n값이 크게 되면, 한 샘플의 평균이 원래 평균에서 크게 벗어나지 않게 된다는 것을 의미한다. 우리가 샘플의 크기를 적당히 크게 잡는 이유는 한 샘플의 평균이 원래의 모집단 평균에서 크게 벗어나지 않기를 바라기 때문이다.만약에 샘플의 숫자(n)을 1로 가정한다면 (n=1), standard error of  의 값은 population의
의 값은 population의 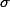 값과 같아지게 된다.
값과 같아지게 된다.
to be finished. . . .
 의 값은 population의
의 값은 population의 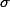 값과 같아지게 된다.
값과 같아지게 된다. to be finished. . . .
2. Summary, e.g., ¶
Central Limit Theorem 을 다시 정리하자면, 아래의 세가지로 요약된다.
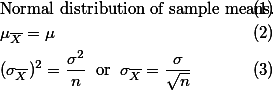
Central Limit Theorem이 사용되는 예를 들어보면 . . . . McDonald 햄버거의 세계시장 공략을 위한 매니저의 역할을 가정해 볼 수 있다.
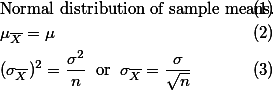
McDonald 본사의 총괄 매니저인 A는 감자튀김의 원료인 감자의 공급자가 일정 수준의 감자를 꾸준하게 공급해 줄 것을 요구하여 왔다. 공급자는 자사의 감자가 평균 200g이며, 표준편차 값이 15라고 주장하였다. 그러나, 웬일인지 요사이 감자 튀김의 매출이 떨어지게 되었는데. . . . A는 공급되는 감자의 품질검사를 실시하기로 한다. . . .
품질 검사를 위해서 모든 감자를 다 체크해 볼 수는 없는 일이다. 샘플을 이용해서 하는 수 밖에 없다는 생각에 우선 A는 공급사인 C사의 말이 사실이라고 가정을 해본다. A는 공급된 감자에서 900개의 감자를 샘플로 뽑아서 이 샘플의 특징( Statistics )을 살펴보고, 이를 통해서 C사의 진실성에 대한 판단을 하기로 한다 (n = 900).
우선, A는 감자를 뽑기 전에 아래와 같은 가정을 한다.
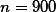 인 감자의 샘플을 계속 뽑아서, 각 샘플의 평균으로 분포도를 만들어 본다면, 이 분포도는 정규분포를 이룰 것이고,
인 감자의 샘플을 계속 뽑아서, 각 샘플의 평균으로 분포도를 만들어 본다면, 이 분포도는 정규분포를 이룰 것이고,
- 샘플 평균들의 평균은 C사가 주장하는 원래 평균인 200g일 것이며,
- 이 특별한 샘플평균 분포의 표준편차(standard deviation 즉, standard error )는
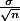 일 것이다. 이를 직접 계산해 보면,
일 것이다. 이를 직접 계산해 보면, 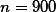 이므로,
이므로, 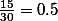 이다.
이다.
A는 여기까지 가정을 한후에 샘플을 뽑아 보았다. 뽑은 결과, 그 평균이 198g 이 나왔다. 이제 A는 이 결과를 가지고 다음과 같이 생각할 수 있다.
Standard error 값이 .5 이므로 2 단위의 standard error 값을 사용하여 범위를 구하여도 199-201 이다. 이는 n=900인 샘플을 취한다고 가정할 때 100번의 샘플링을 한다고 가정하면 95번 (95%) 은 이 범위에서 샘플의 평균이 나온다고 생각할 수 있다. 그런데, 지금 A가 취한 샘플의 평균은 198g이다. 이것이 의미하는 것은 두 가지인데 . . . .
- 100번의 95번에 걸리질 않아서 이번 샘플의 평균이 극단치를 가졌다. 그러나, 이렇게 될 확률은 5%정도 밖에 안된다. . . .
- C사가 거짓말을 하고 있다. 애초 계약인 200g 에 못 미치는 감자를 공급하고 있다. 즉, A는 C사가 거짓말을 하고 있지 않다고 가정하고 정상적인 샘플링을 하였을 때 나타날 수 있는 샘플 평균의 범위를 그려 보았는데 이번 평균은 그 범위를 벗어났으니, 처음 생각인 A는 C사가 거짓말을 하고 있지 않다는 생각을 부정(혹은 기각) 할 수 있다 . 그러나, 이렇게 생각하여도 위의 1번에서의 오류를 무시할 수는 없다. 즉, C사가 거짓말을 하고 있다고 확신하기에는 5%의 '유별난' 샘플링의 확률이 있다. 따라서, 5% 판단의 잘못을 염두에 두고 C사가 거짓말을 한다고 판단하는 것이 옳다.