Estimation of population parameter ¶
두 집단간의 비교, 혹은 모집단의 parameter와 실험처치(treatment)를 준 집단을 비교할 때 우리는 가설검증의 절차를 밟았다 t-test. 이와는 다른 의미로 실험처치를 준 집단의 모집단 parameter를 추정할 경우가 있는데 이를 추정 혹은 Estimation이라고 한다.
추정 혹은 Estimation에는 두 가지 방법이 있다. 첫 번째 방법은 point estimation이라고 한다. 이는 정확한 값을 모집단의 로 추정하는 경우이나 이것이 정확한 경우는 드물다. 두 번째 방법은 interval estimation이라고 하는데, 20권의 책의 무게의 평균으로 전체 모집단의 책의 무게가 어느 범위에 있다라고 추정하는 경우이다.
로 추정하는 경우이나 이것이 정확한 경우는 드물다. 두 번째 방법은 interval estimation이라고 하는데, 20권의 책의 무게의 평균으로 전체 모집단의 책의 무게가 어느 범위에 있다라고 추정하는 경우이다.
추정 혹은 Estimation에는 두 가지 방법이 있다. 첫 번째 방법은 point estimation이라고 한다. 이는 정확한 값을 모집단의
 로 추정하는 경우이나 이것이 정확한 경우는 드물다. 두 번째 방법은 interval estimation이라고 하는데, 20권의 책의 무게의 평균으로 전체 모집단의 책의 무게가 어느 범위에 있다라고 추정하는 경우이다.
로 추정하는 경우이나 이것이 정확한 경우는 드물다. 두 번째 방법은 interval estimation이라고 하는데, 20권의 책의 무게의 평균으로 전체 모집단의 책의 무게가 어느 범위에 있다라고 추정하는 경우이다. 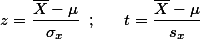
라고 할 때,
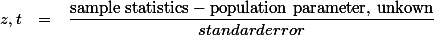
라고 표현할 수 있다.
z-test와 t-test의 경우,
![\begin{eqnarray}
z & = & \frac{\overline{X}-\mu}{\sigma_{x}} \nonumber \\
z\sigma_{x} & = & \overline{X} - \mu \nonumber \\
\mu + z \sigma_{x} & = & \overline{X} \nonumber \\
\mu & = & \overline{X} - [z \sigma_{x}]
\end{eqnarray}
\begin{eqnarray}
z & = & \frac{\overline{X}-\mu}{\sigma_{x}} \nonumber \\
z\sigma_{x} & = & \overline{X} - \mu \nonumber \\
\mu + z \sigma_{x} & = & \overline{X} \nonumber \\
\mu & = & \overline{X} - [z \sigma_{x}]
\end{eqnarray}](/_cache/latex/7/7b/a09eab4c85d7b5638eacfd2bf67b1c45.png)
![\begin{eqnarray}
t & = & \frac{\overline{X}-\mu}{s_x} \nonumber \\
t s_x & = & \overline{X} - \mu \nonumber \\
\mu + t \sigma_{x} & = & \overline{X} \nonumber \\
\mu & = & \overline{X} - \left[ t s_x \right]
\end{eqnarray}
\begin{eqnarray}
t & = & \frac{\overline{X}-\mu}{s_x} \nonumber \\
t s_x & = & \overline{X} - \mu \nonumber \\
\mu + t \sigma_{x} & = & \overline{X} \nonumber \\
\mu & = & \overline{X} - \left[ t s_x \right]
\end{eqnarray}](/_cache/latex/7/75/3ae85adf57992d60313b3e5eadda2204.png)
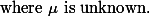
즉,  (population parameter)에 대한 추정은
(population parameter)에 대한 추정은
 (population parameter)에 대한 추정은
(population parameter)에 대한 추정은 ![$ \overline{X}- \left[ \pm (z,t) (\sigma_x, s_x)\right] $ $ \overline{X}- \left[ \pm (z,t) (\sigma_x, s_x)\right] $](/_cache/latex/9/9c/0afc0d9ddcf4b3fec24833871d57f68d.png) 이다. 여기서
이다. 여기서 -> 추청 (estimation)될 값, unknown
-> 추청 (estimation)될 값, unknown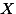 -> 얻어진 값 (observed value)
-> 얻어진 값 (observed value)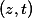 -> unknown till determination
-> unknown till determination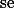 -> 계산가능
-> 계산가능Point estimation을 위해서 우리는 z, t = 0 의 값을 이용하여 population의  값을 추정할 수 있다. 이렇게 얻는 값은 sample의 평균값,
값을 추정할 수 있다. 이렇게 얻는 값은 sample의 평균값,  가 된다. z, t = 0 의 값을 사용하는 까닭은 z-distribution 혹은 t-distribtuion에서 중앙 값 (즉, 평균)에 해당하는 값이 0 이기 때문이다. Interval estimation을 위해서는, z, t 값을 연구자가 정하게 된다. 이렇게 정해지는 구간을 ConfidenceLevel 이라고 하며, 이 구간을 ConfidenceInterval 혹은 ConfidenceInterval CL이라고 한다. 예를 들면, CL을 95%로 한다면, z = 2 가 될 터이고, t 값은 95% 의 확신을 뒤집은 5% 의 오류가능성과 df (n-1) 값에 해당하는 t-distribution table의 값 (
가 된다. z, t = 0 의 값을 사용하는 까닭은 z-distribution 혹은 t-distribtuion에서 중앙 값 (즉, 평균)에 해당하는 값이 0 이기 때문이다. Interval estimation을 위해서는, z, t 값을 연구자가 정하게 된다. 이렇게 정해지는 구간을 ConfidenceLevel 이라고 하며, 이 구간을 ConfidenceInterval 혹은 ConfidenceInterval CL이라고 한다. 예를 들면, CL을 95%로 한다면, z = 2 가 될 터이고, t 값은 95% 의 확신을 뒤집은 5% 의 오류가능성과 df (n-1) 값에 해당하는 t-distribution table의 값 ( 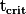 ) 이라고 하겠다. 즉, t값은 sample size와 (df) CL에 따라서 변하게 되며, z값은 CL에 따라서 변하게 된다. 예를 또 들자면, 위에서 CL을 99%로 하게되면, z값은 3 이 될것이다. t값의 경우,
) 이라고 하겠다. 즉, t값은 sample size와 (df) CL에 따라서 변하게 되며, z값은 CL에 따라서 변하게 된다. 예를 또 들자면, 위에서 CL을 99%로 하게되면, z값은 3 이 될것이다. t값의 경우, 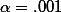 와 df(n-1)의 값에 해당하는 값을 갖게 된다.
와 df(n-1)의 값에 해당하는 값을 갖게 된다.
 값을 추정할 수 있다. 이렇게 얻는 값은 sample의 평균값,
값을 추정할 수 있다. 이렇게 얻는 값은 sample의 평균값,  가 된다. z, t = 0 의 값을 사용하는 까닭은 z-distribution 혹은 t-distribtuion에서 중앙 값 (즉, 평균)에 해당하는 값이 0 이기 때문이다. Interval estimation을 위해서는, z, t 값을 연구자가 정하게 된다. 이렇게 정해지는 구간을 ConfidenceLevel 이라고 하며, 이 구간을 ConfidenceInterval 혹은 ConfidenceInterval CL이라고 한다. 예를 들면, CL을 95%로 한다면, z = 2 가 될 터이고, t 값은 95% 의 확신을 뒤집은 5% 의 오류가능성과 df (n-1) 값에 해당하는 t-distribution table의 값 (
가 된다. z, t = 0 의 값을 사용하는 까닭은 z-distribution 혹은 t-distribtuion에서 중앙 값 (즉, 평균)에 해당하는 값이 0 이기 때문이다. Interval estimation을 위해서는, z, t 값을 연구자가 정하게 된다. 이렇게 정해지는 구간을 ConfidenceLevel 이라고 하며, 이 구간을 ConfidenceInterval 혹은 ConfidenceInterval CL이라고 한다. 예를 들면, CL을 95%로 한다면, z = 2 가 될 터이고, t 값은 95% 의 확신을 뒤집은 5% 의 오류가능성과 df (n-1) 값에 해당하는 t-distribution table의 값 ( 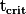 ) 이라고 하겠다. 즉, t값은 sample size와 (df) CL에 따라서 변하게 되며, z값은 CL에 따라서 변하게 된다. 예를 또 들자면, 위에서 CL을 99%로 하게되면, z값은 3 이 될것이다. t값의 경우,
) 이라고 하겠다. 즉, t값은 sample size와 (df) CL에 따라서 변하게 되며, z값은 CL에 따라서 변하게 된다. 예를 또 들자면, 위에서 CL을 99%로 하게되면, z값은 3 이 될것이다. t값의 경우, 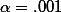 와 df(n-1)의 값에 해당하는 값을 갖게 된다.
와 df(n-1)의 값에 해당하는 값을 갖게 된다.Q,인 모집단이 존재한다. 이 집단에서 뽑은 샘플 (n=25) 에 treatment를 가한 후의 점수를 보니,
이었다. treatment를 받은 이 집단의 진짜(모집단) 평균을 추정하라.
A,