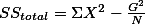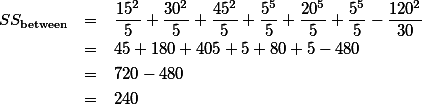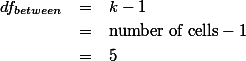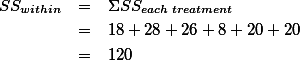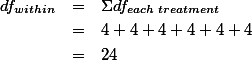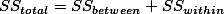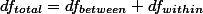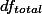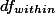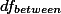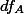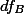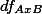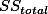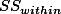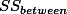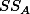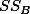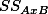1. Factorial Design ¶
t-test와 ANOVA의 섹션까지 다룬것은 모두 하나의 독립변인(IndependentVariable)과 하나의 종속변인(DependentVariable) 간의 관계에 대한 규명을 하는 것이었다.
실제 연구를 하는 경우 이와 같이 하나씩의 독립변인과 종속변인으로 이루어진 검증을 하기보다는 여러가지 다른 원인을 종합적으로 살펴보는 때가 많다. 즉, 연구자는 실험참가자의 행동이나 반응으로 나타나는 종속변인의 원인을 하나의 독립변인이 아닌 여러가지 (대개는 2가지) 독립변인을 놓고 살펴본다는 것이다.
이와 같은 연구를 Factorial Design이라고 한다.
2개의 독립변인과 하나의 종속변인으로 이루어진 디자인이라면 Two-factor design이라고 부를 수 있다.
1.1. 예 ¶
여름에는 작업 능률이 떨어진다고 한다. 왜냐 하면, 덥기 때문이다. 그러나, 종종 사람들은 더운 것은 참을 수 있으나 습도가 높은 것은 참을 수 없다고 한다. 즉, 작업능률을 저하하는데 작용하는 (영향을 미치는) 요소로 2가지가 포함될 수 있다. 하나는 온도이고 하나는 습도이다. 아래 표는 이를 위한 실험에 대한 결과를 표로 요약한 것이다. 표가 의미하는 것은 이 연구가 6개의 특별한 상황 (2가지의 독립변인으로 인해서 일어나는)에 따른 작업능률의 (한가지의 종속변인) 변화에 대한 파악이다.
위의 상황에서 독립변인의 분석을 한다고 하면, 연구자가 관심을 갖고 살펴보게 되는 부분으로
| Factor B: Temperature | ||||
| Factor A: Humidity | 24 | 29 | 34 | |
| 30% | n=15 24도 30% | n=15 29도 30% | n=15 34도 30% | |
| 70% | n=15 24도 70% | n=15 29도 70% | n=15 34도 70% | |
위의 상황에서 독립변인의 분석을 한다고 하면, 연구자가 관심을 갖고 살펴보게 되는 부분으로
1. 습도의 변화 (2가지, 30%와 70%)에 따른 차이
2. 온도의 변화 (3가지, 24, 29, 34도)에 따른 차이
3. 위의 두 가지 변화로 설명되지 않는다고 나타나는 차이 (만약에 존재한다면) = 즉, 두 가지 독립변인의 동시존재에 의해서만 나타나는 차이
2. 온도의 변화 (3가지, 24, 29, 34도)에 따른 차이
3. 위의 두 가지 변화로 설명되지 않는다고 나타나는 차이 (만약에 존재한다면) = 즉, 두 가지 독립변인의 동시존재에 의해서만 나타나는 차이
를 보는 것이 된다. 따라서, 가설테스트의 입장에서 보면, 연구자는 한가지 문제에 대한 3가지 가설을 테스트하는 것이 된다. 이를 풀어서 이야기 하자면, 1) 습도의 영향력 2) 온도의 영향력 3) 두가지가 동시존재함으로써 나타나는 영향력 에 대한 테스트이다.
얼뜻 보면, 복잡한듯 하지만, 위의 테스트 또한 F-test (ANOVA)를 이용하여 해결할 수 있으며, 이는 아래와 같이 나타낼 수 있다.
![$F = \frac{\text{variance (differences) between sample means}}{\text{variance (difference) expected by chance}} \cdots [1]$ $F = \frac{\text{variance (differences) between sample means}}{\text{variance (difference) expected by chance}} \cdots [1]$](/_cache/latex/a/ab/08f5016a69001c135a62fea0ffef3060.png)
1.2. 주효과 (Main effects) ¶
| Factor B: Temperature | |||||
| Factor A: Humidity | 24 | 29 | 34 | ||
| 30% |  |  |  |  | |
| 70% |  |  |  |  | |
 |  |  | |||
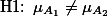
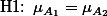
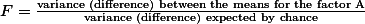
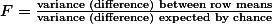
반면에, Factor B: Temperature에 관한 가설은:
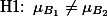 혹은
혹은
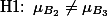 혹은
혹은
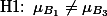 혹은
혹은
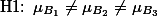
와 같이 정리될 수 있는데, 한가지 현상에 대한 가설을 여러번에 나누어서 설명하는 것은 복잡하므로 아래와 같이 요약해 볼 수 있다.
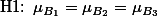
다시, 이에 대한 F-test는
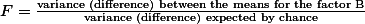
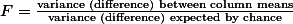
와 같이 정리할 수 있다.
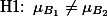 혹은
혹은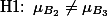 혹은
혹은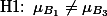 혹은
혹은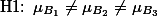
H1: 적어도 한 평균값이 다른 평균값과 다를 것이다.
이에 대한 영가설은 비교적 쉽게 표현된다: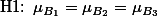
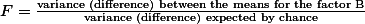
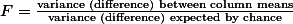
즉, 연구자는 각 독립변인의 특성에 대한 그룹의 분산 간 차이를 비교하여 봄으로써, 각각의 팩터(독립변인)의 효과를 살펴볼 수 있다. 이를 각각 Factor A에 대한 주효과 (Main effect)와 Factor B에 대한 주효과 (Main effect)라고 이야기 할 수 있다.
1.3. 상호효과 (Interaction effects) ¶
아래의 테이블은 위의 실험결과를 약간 변형한 것인데, 각각의 독립변인 (팩터)에 대한 평균값은 이전의 테이블과 동일하다.
| Factorial ANOVA | |||||
| Factor B: Temperature | |||||
| Factor A: Humidity | 24 | 29 | 34 | ||
| 30% |  |  |  |  | |
| 70% |  |  |  |  | |
 |  |  | |||
이를 다시 F-test의 공식에 적용시켜서 정리해보면:
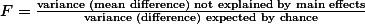
와 같다.
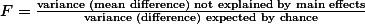
이를 가설로 정리를 해보자면
H1: A팩터와 B팩터 간의 상호작용이 존재한다. 즉, 각각의 상태에 따라서 나타나는 평균의 차이가 두 팩터가 갖는 주효과에 의해서만 설명되지 않고 부가적으로 더 있다.
H0: A팩터와 B팩터 간의 상호작용은 존재하지 않는다. 즉, 각각의 상태에 따라서 나타나는 평균의 차이는 두 팩터가 갖는 주효과에 의해서만 설명된다.
와 같이 정리할 수 있다. H0: A팩터와 B팩터 간의 상호작용은 존재하지 않는다. 즉, 각각의 상태에 따라서 나타나는 평균의 차이는 두 팩터가 갖는 주효과에 의해서만 설명된다.
그러나, 사실 위의 표의 해석이 그리 직관적이지는 않다. 상호의존적이라는 단어가 의미하는 것이 그리 직관적이지 않기 때문이다. 이럴 경우, 흔히 연구자는 위의 표를 아래와 같은 도표로 바꾸어 살펴보게 되는데, 이렇게 하는 이유는 상호효과(InteractionEffect)의 존재여부가 완연히 들어나기 때문이다.
| Examining Interaction Effect | |
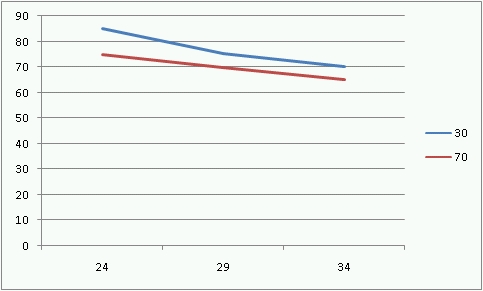 Figure 1. Case 1 [JPG image (32.27 KB)] | 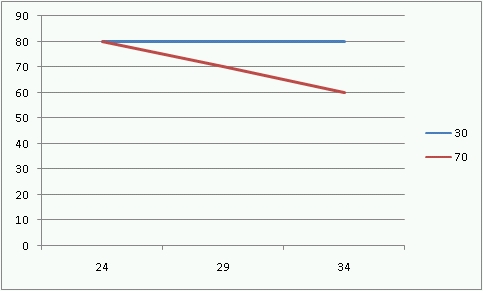 Figure 2. Case 2 [JPG image (29.96 KB)] |
그림1과 2의 붉은색선과 푸른색선은 각각 습도의 차이(30%와 70%)를 나타내며 x축은 온도의 차이를 나타낸다. 1의 경우, 두 선은 서로 평행하여 겹치지 않는데 이것이 의미하는 것은 두 요인의 영향력이 서로 독립적으로 나타난다는 뜻이다. 반면에 오른쪽의 그림2는 두선이 평행하지 않는데, 이는 두 요인이 상호의존적으로 작용하기 때문이다. 이 경우에는 온도의 영향은 오직 습도가 높을때에만 나타난다.
1.4. e.g., ¶
| Main effect for factor A but no main effect for factor B | ||||
| B1 | B2 | |||
| A1 | 20 | 20 | MA1 = 20 | 10-point difference |
| A2 | 10 | 10 | MA2 = 10 | |
| MB1 = 15 | MB2 = 15 | |||
| No difference | ||||
| Main effect for both factor A and factor B | ||||
| B1 | B2 | |||
| A1 | 10 | 30 | MA1 = 20 | 10-point difference |
| A2 | 20 | 40 | MA2 = 30 | |
| MB1 = 15 | MB2 = 35 | |||
| 20-point difference | ||||
| No main effect for either factor A and factor B | ||||
| B1 | B2 | |||
| A1 | 10 | 20 | MA1 = 15 | no difference |
| A2 | 20 | 10 | MA2 = 15 | |
| MB1 = 15 | MB2 = 15 | |||
| - - - - no difference - - - - | ||||
1.5. 2 Factor ANOVA test ¶
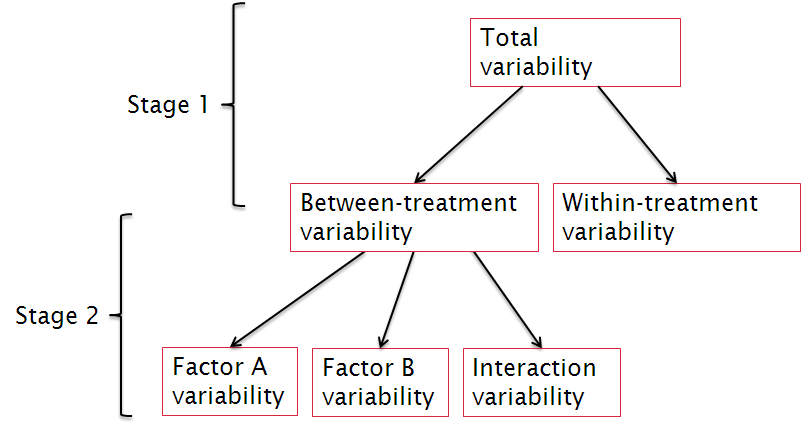
Figure 1. Case 1 [JPG image (127.03 KB)]
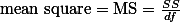
| Factor B | ||||||
| Factor A | 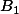 | 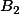 |  |    | ||
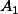 | 3 | 2 | 9 |  | ||
| 1 | 5 | 9 | ||||
| 1 | 9 | 13 | ||||
| 6 | 7 | 6 | ||||
| 4 | 7 | 8 | ||||
| T=15 | T=30 | T=45 | ||||
| SS=18 | SS=28 | SS=26 | ||||
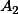 | 0 | 3 | 0 | 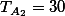 | ||
| 2 | 8 | 0 | ||||
| 0 | 3 | 0 | ||||
| 0 | 3 | 5 | ||||
| 3 | 3 | 0 | ||||
| T=5 | T=20 | T=5 | ||||
| SS=8 | SS=20 | SS=20 | ||||
 | 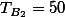 | 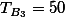 | ||||
1.5.2. Stage 2 ¶
- For factor A.
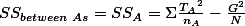
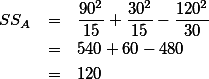
위의 표에서,
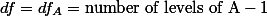

- For factor B.
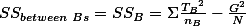
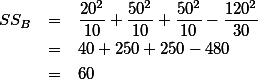
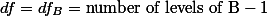

- For interaction (A X B).
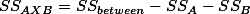
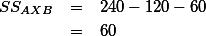
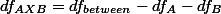
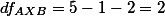
And,
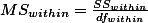
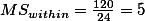
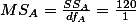
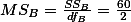
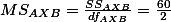
Finally,

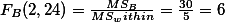
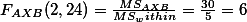
Check![[http]](http://wiki.commres.org/imgs/http.png) F distribution table(http://commres.net/wiki/_media/ftable.pdf)
F distribution table(http://commres.net/wiki/_media/ftable.pdf)
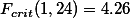
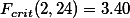
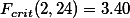
1.6. Check ¶
| Factor B: Temperature | |||||
| Factor A | B1 | B2 | B3 | ||
| A1 | n=10 T=0 SS=30 | n=10 T=10 SS=40 | n=10 T=20 SS=50 | ||
| A2 | n=10 T=40 SS=60 | n=10 T=30 SS=50 | n=10 T=20 SS=40 | ||
- Calculate the totals for each level of factor A, and compute SS for factor A.
- Calculate the totals for factor B, and compute SS for the factor
- Given that the between-treatments SS is equal to 100, what is the SS for the interaction?
- Calculate the within-treatments SS, df, and MS for these data.
1.7. e.g., ¶
| Weight | Fullness | nCookies |
| 1 | 1 | 15 |
| 1 | 1 | 17 |
| 1 | 1 | 32 |
| 1 | 1 | 12 |
| 1 | 1 | 34 |
| 1 | 1 | 27 |
| 1 | 1 | 13 |
| 1 | 1 | 24 |
| 1 | 1 | 41 |
| 1 | 1 | 20 |
| 1 | 1 | 23 |
| 1 | 1 | 25 |
| 1 | 1 | 9 |
| 1 | 1 | 21 |
| 1 | 1 | 22 |
| 1 | 1 | 26 |
| 1 | 1 | 26 |
| 1 | 1 | 28 |
| 1 | 1 | 22 |
| 1 | 1 | 3 |
| 1 | 2 | 22 |
| 1 | 2 | 7 |
| 1 | 2 | 15 |
| 1 | 2 | 6 |
| 1 | 2 | 8 |
| 1 | 2 | 18 |
| 1 | 2 | 24 |
| 1 | 2 | 19 |
| 1 | 2 | 11 |
| 1 | 2 | 9 |
| 1 | 2 | 24 |
| 1 | 2 | 19 |
| 1 | 2 | 9 |
| 1 | 2 | 19 |
| 1 | 2 | 29 |
| 1 | 2 | 9 |
| 1 | 2 | 18 |
| 1 | 2 | 17 |
| 1 | 2 | 3 |
| 1 | 2 | 14 |
| 2 | 1 | 7 |
| 2 | 1 | 19 |
| 2 | 1 | 8 |
| 2 | 1 | 23 |
| 2 | 1 | 6 |
| 2 | 1 | 11 |
| 2 | 1 | 18 |
| 2 | 1 | 23 |
| 2 | 1 | 22 |
| 2 | 1 | 16 |
| 2 | 1 | 28 |
| 2 | 1 | 19 |
| 2 | 1 | 2 |
| 2 | 1 | 27 |
| 2 | 1 | 20 |
| 2 | 1 | 25 |
| 2 | 1 | 23 |
| 2 | 1 | 10 |
| 2 | 1 | 19 |
| 2 | 1 | 14 |
| 2 | 2 | 14 |
| 2 | 2 | 21 |
| 2 | 2 | 16 |
| 2 | 2 | 14 |
| 2 | 2 | 17 |
| 2 | 2 | 20 |
| 2 | 2 | 20 |
| 2 | 2 | 21 |
| 2 | 2 | 32 |
| 2 | 2 | 26 |
| 2 | 2 | 9 |
| 2 | 2 | 14 |
| 2 | 2 | 16 |
| 2 | 2 | 15 |
| 2 | 2 | 6 |
| 2 | 2 | 5 |
| 2 | 2 | 12 |
| 2 | 2 | 23 |
| 2 | 2 | 27 |
| 2 | 2 | 32 |
| Factor B: Fullness | |||||
| Factor A: Weight | Empty | Full | |||
| Normal | n=20 T=440 SS=1502 | n=20 =15 =15 T=300 SS=940 | 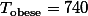 | ||
| Obese | n=20 = 17 = 17 T=340 SS=1062 | n=20 = 18 = 18T=360 SS=1084 | 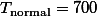 | ||
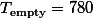 |  | G=1440 N=80  | |||
- step 1. Build hypotheses
- step 2. Locate the critical range for F-ratio. calculate the
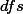
- Comput F-ratio
SS
MS 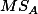
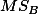
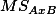
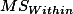
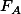
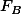
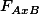
- Make decision
| Result | ||||
| Source | SS | df | MS | F |
| Between treatment | ||||
| Factor A (weight) | ||||
| Factor B (fullness) | ||||
| A x B interaction | ||||
| Within treatment | ||||
| Total | ||||
| weigth x fullness factorial design | ||||
- In the literature (APA style)
The means and standard deviations are presented in Table 1. The two-factor analysis of variance showed no significant main effect for the weight factor, F(x,xx)=xxx, p>.05; and no significant main effect for the fullness factor, F(x,xx)=xxx, p>.05; but the interaction between weight and fullness was significant, F(x,xx)=xxx, p<.05.
| Table 1 Mean number of crackers eaten in each treatment condition | |||
| Fullness | |||
| Weight | Empty stomach | Full stomach | |
| Normal | M=22 SD=9.00 | M=15 SD=8.18 | |
| Obese | M=17 SD=8.34 | M=18 SD=8.16 | |
1.8. Interpreting interaction ¶
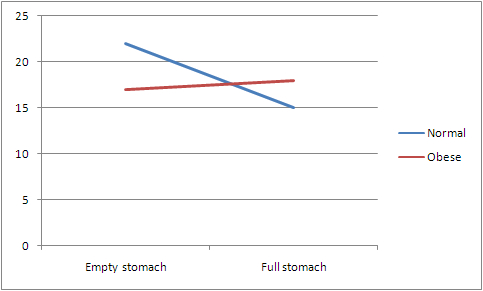
Figure 3. A graph showing the interaction between the two factor [JPG image (32.07 KB)]
1.9. e.g., ¶
| Influence of urine chemicals to other male & female rats | ||||
| Factor B: Amount of chemical | ||||
| Factor A: gender | None | Small | Large | |
| Male | n=5 T=10 SS=15 | n=5 T=20 SS=19 | n=5 T=30 SS=31 | |
| Female | n=5 T=10 SS=15 | n=5 T=20 SS=19 | n=5 T=30 SS=31 | |
 | ||||
Build hypotheses. Use ANOVA with critical level = .05 to test the researcher's hypotheses.