1. probability ¶
사건 A가 일어날 확율(probability)는 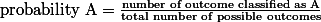 라고 표현할 수 있다. 따라서, 카드에서 spade가 나올 확율은
라고 표현할 수 있다. 따라서, 카드에서 spade가 나올 확율은 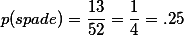 이고, 동전의 앞면(head)이 나올 확율은
이고, 동전의 앞면(head)이 나올 확율은 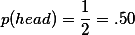 이다.
이다.
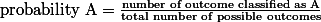 라고 표현할 수 있다. 따라서, 카드에서 spade가 나올 확율은
라고 표현할 수 있다. 따라서, 카드에서 spade가 나올 확율은 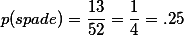 이고, 동전의 앞면(head)이 나올 확율은
이고, 동전의 앞면(head)이 나올 확율은 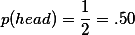 이다.
이다.
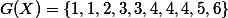 일때
일때 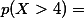 의 값은?
의 값은?
 이고,
이고, 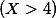 의 경우의 갯수는 2 이므로,
의 경우의 갯수는 2 이므로,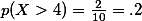 이다.
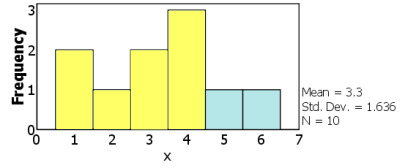
이다. 그렇다면, 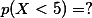
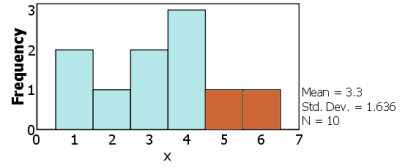
[PNG image (9.94 KB)]
[PNG image (9.95 KB)]
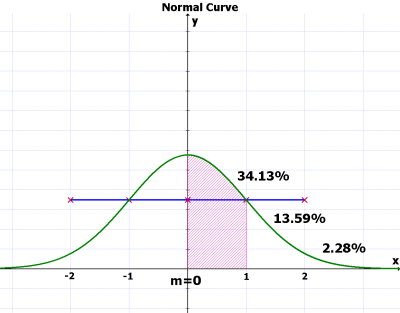
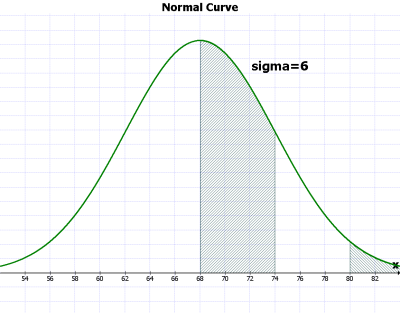
1.3. Normal distribution ¶
[PNG image (31.3 KB)]
Normal distribution의 특징:
- 그래프의 좌우가 대칭 (symmetry)
- (mean = median = mode) 이며, 오른쪽 반 = 전체의 50% (.5)
- 양극의 숫자는 가운데의 숫자에 비교하여 드물다.
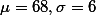 일때,
일때, 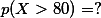
[PNG image (52.42 KB)]
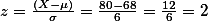
따라서, 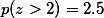 % 이다. 이것이 의미하는 것은 이 분포에서 점수 80을 넘는 사람들의 퍼센티지는 약 2.5% 즉 100명 중 2.5명 꼴이라는 것이다.
% 이다. 이것이 의미하는 것은 이 분포에서 점수 80을 넘는 사람들의 퍼센티지는 약 2.5% 즉 100명 중 2.5명 꼴이라는 것이다.
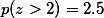 % 이다. 이것이 의미하는 것은 이 분포에서 점수 80을 넘는 사람들의 퍼센티지는 약 2.5% 즉 100명 중 2.5명 꼴이라는 것이다.
% 이다. 이것이 의미하는 것은 이 분포에서 점수 80을 넘는 사람들의 퍼센티지는 약 2.5% 즉 100명 중 2.5명 꼴이라는 것이다.z-table을 이용하면, 어떤 score에서라도 그 score 전후의 면적을 구하여, probability를 알 수 있다.
- z-table에 의하면 z-score 0-2까지의 면적은: 0.4772
- 따라서, 2에서 그 이상까지의 면적은 0.5-0.4772= ...
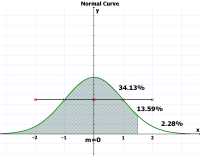
e.g., Normal distiribution에서 z=1.5 보다 작은 점수를 받은 샘플의 퍼센티지는?
[PNG image (10.97 KB)]
- p(z<0) = 0.5
- p(0<z<1.5) = 0.4332
SAT score: mean=500, stdev=100 일때, p(S>650) = ?
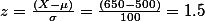 따라서,
따라서, 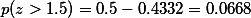 or 6.68%
or 6.68%위에서 p(600<s<700) = ?
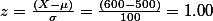
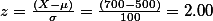
p(s>600)= 0.5-0.3413=0.1587
p(s>700)= 0.5-0.4772=0.0228
p(s>700)= 0.5-0.4772=0.0228
따라서, p(1 < z < 2) = 0.1587 - 0.0228 = 0.1359 or 13.59%
Q: 위의 예에서, 상위 16%에 들기 위한 최소의 점수는?
우리가 가진 table은 0-x.xx의 범위를 기준으로 하는 table이므로 상위 16%는 0에서 z-score 값이 약 34%일 경우의 zscore를 의미한다. 이 z-score는 약 1. 따라서, 필요한 최소의 점수는 평균값에 standard deviation값 하나를 더한 것, 즉, 600점이 된다.
1.6. check point ¶
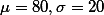 의 모집단이 있을 때; 샘플숫자를 16 (n=16) 으로 하는 샘플들의 distirubtion 에 대해서 이야기 해보시오.
의 모집단이 있을 때; 샘플숫자를 16 (n=16) 으로 하는 샘플들의 distirubtion 에 대해서 이야기 해보시오. - the distribution of sample means는 normal distribution을 이룰 것이며,
- 그 평균은 모집단 평균(
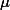 )인 80일 것이고,
)인 80일 것이고,
- Standard deiviation 값은
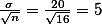 일 것이다.
일 것이다.
위의 예에서 밝힌 사실이 의미하는 것을 서술하시오.
----샘플사이즈가 커질 수록 standard error값도 같이 커진다.
----어떤 조건이 만족하여야, 샘플평균값들의 분포(distribution of sample means)가 정규분포를 이루는가?
1.7. Probability and distribution of smaple means ¶
Population of SAT score ( 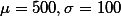 ) 이다.
) 이다.  의 샘플을 뽑는다고 가정을 하면, 그 샘플의 평균이 540보다 같거나 클 확율(probability)은 어떻게 되는가?
의 샘플을 뽑는다고 가정을 하면, 그 샘플의 평균이 540보다 같거나 클 확율(probability)은 어떻게 되는가?
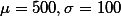 ) 이다.
) 이다.  의 샘플을 뽑는다고 가정을 하면, 그 샘플의 평균이 540보다 같거나 클 확율(probability)은 어떻게 되는가?
의 샘플을 뽑는다고 가정을 하면, 그 샘플의 평균이 540보다 같거나 클 확율(probability)은 어떻게 되는가?- 샘플(n=25)을 계속 취해서 그 평균값의 distribution을 보면, normal distribution
- Distribution의 평균은 500
- Distribution의 standard error 값은

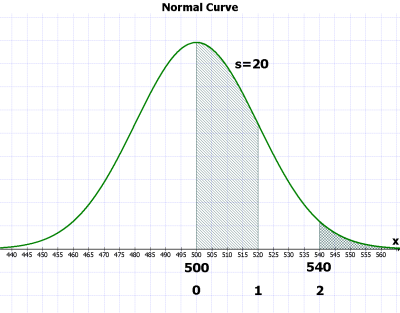
[PNG image (55.09 KB)]
즉, 위의 그래프에서 stdev unit의 값은 20이고 540은 평균인 500에서 2 unit만큼 떨어져 있으므로 구해야 할 값은 p(s>2) = ?
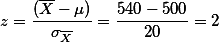
위의 예가 의미하는 것은 population의 parameter가 위와 같고, n=25인 샘플을 뽑는다면, 그 샘플의 평균값이 나올 확률의 분포는 위의 그래프와 같다는 것이다. 즉 샘플을 한 번 뽑아서 그 평균이 540 이상일 확률은 약 2.5%이다 (5%의 반값).
(-2<z<2) 구간을 생각해보면, 이 구간은 약 95%이다. 이것이 의미하는 것은 n=25인 샘플을 뽑을 때, 그 샘플의 평균이 460에서 540이 될 확률은 약 95%라는 것이다. 즉, 다시 말하면, 100 중 95는 그 샘플의 평균값이 460-540일 것이라고 이야기 하는 것이 된다.
이렇게 population의 parameter를 알고 sample의 size를 알 때, 우리는 그 샘플의 평균이 어느 범위에 들지를 예측할 수 있다.
샘플사이즈가 중요한 이슈가 되는 이유는 샘플사이즈 변화에 따른 sampling error의 변화를 보면 알 수 있다.
우선 위에서, 우리는
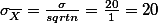
for sample size = 4,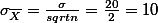
for sample size = 100,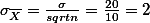
Q: Population의 parameter: 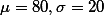 일 때, 샘플 사이즈가 각각, 1, 4, 100의 sampling error of
일 때, 샘플 사이즈가 각각, 1, 4, 100의 sampling error of 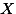 를 구하보라.
를 구하보라.
- 샘플평균의 분포 (distribution of sample means)가 정상분포이고;
- 샘플평균들의 평균은 모집단의 평균값과 같을 것이라는 사실을 이전의 학습을 통해서 알 고 있다.
- 세 샘플 종류의 차이점은 variability에 있다.
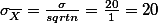
for sample size = 4,
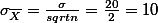
for sample size = 100,
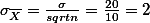
이 것을 그래프로 그려보면 다음과 같다.
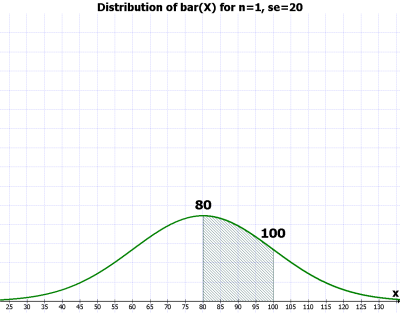
그림. n = 1, se = 20

[PNG image (39.15 KB)]
그림. n = 1, se = 20
[PNG image (38.19 KB)]
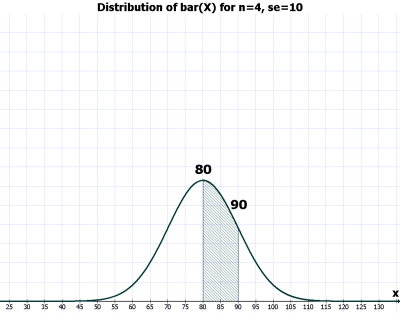
그림. n = 4, se = 10
[PNG image (35.09 KB)]
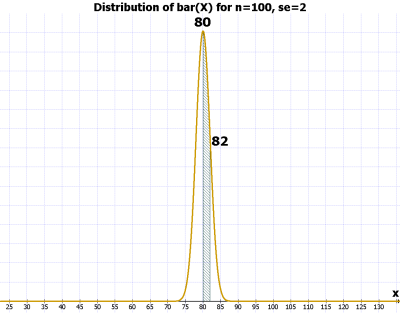
그림. n = 1, se = 2
여기서 반드시 이해해야 할 점은: population ( 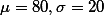 ) 에서,
) 에서,
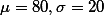 ) 에서,
) 에서,- 그림 1의 경우, 샘플의 숫자가 1인 샘플을 뽑았을 때, 그 샘플의 평균(여기서는 그 샘플의 값)은 95%의 확률을 가지고, 40 - 120 (80-40 - 80+40) 사이에서 발견될 것이라는 것.
- 그림 2의 경우는 같은 확률로 60 - 100;
- 그림 3의 경우에, 같은 활률로 76-84에서 발견될 것이라는 점이다.
만약에 샘플의 숫자를 1600으로 하면 sampling error of sample means는 20/40, 즉, 1/2로 좁혀지고, 따라서, 현실적으로 샘플을 취하면(n=1600), 그 샘플의 평균값은 100중 95로 80 +- 1 로 좁혀지게 된다.
만약에 샘플의 숫자를 2500으로 하면 sampling error of sample means는 20/50, 즉, 4/10로 좁혀지고, 따라서, 현실적으로 샘플을 취하면(n=2500), 그 샘플의 평균값은 100중 95로 80 +- 0.8로 좁혀지게 된다.
2.1. Errors in decision making ¶
위에서 강사가 샘플의 statistics와 population parameter를 근거로 일종의 의사결정(decision-making)을 하였다. 잠시 이 procedure를 살펴 보면, 강사의 의사결정에는 일종의 틀릴 여지가 있음을 알 수 있다. 이는 두 가지로 나눠질 수 있는데, 이를 각각 TypeIError 와 TypeIIError라고 부른다.
2.1.1. Type I Error ¶
가령 case A의 경우, 샘플에서 얻은 z-score는 3이었고, 이는 z-score = 2 를 벗어나는 곳에 존재함으로, 강사는 이 샘플의 평균값은 보통 population에서 취해진 샘플의 평균값으로서는 unusual하다는 주장을 하였다. 그러나, 보통 population에서 취해지는 샘플이라도 그 z-score가 2를 넘어서는 것이 전무한 것은 아니다. z-score = 2 를 기준으로 하는 extreme 샘플의 경우, 약 5%가 이에 해당한다. 다시 말하면, 강사가 얻은 샘플의 z-score = 3이 바로 이 5%에 해당하는 경우라면, 강사의 null hypothesis의 rejection은 틀린 것이 되고만다. 이와 같은 error를 Type I error라고 한다. 사실은 wiki가 효과가 없는데, 있다는 결론을 내린 것이다.
2.1.2. Type II Error ¶
case B의 경우는, 샘플에서 얻은 z-score는 1이었다. 이것이 의미하는 것은 wiki를 사용하지 않는 보통의 population에서 나오는 sample이라면 대개(95%) 가질 수 있는 샘플의 평균을 강사의 샘플이 가졌다는 의미이므로, 강사는 이를 근거로 wiki의 효과가 없었다는 결론을 내렸다. 하지만, Type I 에러와 마찬가지로 강사의 이런 주장이 오류에 근거할 여지가 있다. 흔한 예로, 샘플의 숫자가 적은 편이고, 효과가 눈에 뜨게 크지 않는 경우, 이런 오류가 나타난다. Type I 오류와는 다르게, Type II 오류가 치명적인 것은 아니다.
- 가령 n=16인 샘플(SA)과 n=100인 샘플(SB)을 생각해보면, SA의 standard error 값은 SB의 그것보다 상대적으로 크다 (즉, SA의 95% region이 상대적으로 넓다). 따라서, 샘플의 평균값이 critical region이 아닌 region에 걸려 있을 확률이 많다.