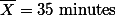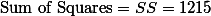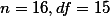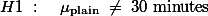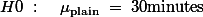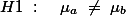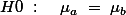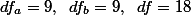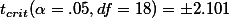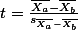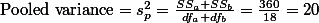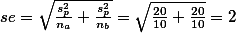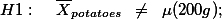1.1. 모집단의 평균과 표준편차를 알고 있을 때 ¶
모집단을 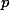 , 모집단의 평균을
, 모집단의 평균을  모집단의 표준편차를
모집단의 표준편차를 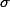 라고 하고, 이 둘을 알고 있을 때 sample을 추출해서 모집단의
라고 하고, 이 둘을 알고 있을 때 sample을 추출해서 모집단의  와
와 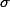 를 확인하는 방법이 있다. 흔히 Quality control에 많이 사용된다.
를 확인하는 방법이 있다. 흔히 Quality control에 많이 사용된다.
감자의 단위당 무게가 평균 200g이고 표준편차가 20이라고 주장하는 납품업자로부터 감자의 quality가 보고와 일치하는 지 궁금하여 샘플 (n=400)을 뽑아 확인한다.

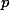 , 모집단의 평균을
, 모집단의 평균을  모집단의 표준편차를
모집단의 표준편차를 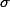 라고 하고, 이 둘을 알고 있을 때 sample을 추출해서 모집단의
라고 하고, 이 둘을 알고 있을 때 sample을 추출해서 모집단의  와
와 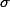 를 확인하는 방법이 있다. 흔히 Quality control에 많이 사용된다.
를 확인하는 방법이 있다. 흔히 Quality control에 많이 사용된다.감자의 단위당 무게가 평균 200g이고 표준편차가 20이라고 주장하는 납품업자로부터 감자의 quality가 보고와 일치하는 지 궁금하여 샘플 (n=400)을 뽑아 확인한다.
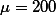 ,
, 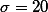

- 위의 정보(se)는
- 샘플의 숫자(n)가 400인 샘플을 뽑았을 때,
- 그 샘플의 평균값이 나타날 수 있는 범위를 정해주는 단위
- se = 1 이므로
- 샘플의 숫자(n)가 400인 샘플을 뽑았을 때,
- 400개의 샘플을 뽑았을 때, 그 샘플의 평균은 평균 200g을 기준으로 좌우로 2단위의 se만큼 떨어진 범위에서 발견될 것이다.
- se의 두 단위를 사용하였으므로, 좌우 범위는 각각 2이다.
- 즉, 198g - 202g에서 샘플의 평균이 나올 것이다.
- 마지막으로 이 범위에서 샘플의 평균이 발견될 확률은 95% 이다. 이유는 stadnard deviation of sample means = standard error = se 를 2 단위 썻기 때문이다.
- 즉, 우리는 400개의 샘플을 뽑았을 때, 그 샘플의 평균이 198에서 202일 거라는 확신을 95%하게됨.
- 마지막으로 샘플을 뽑아서 예상대로 보면 됨. 샘플의 평균이 196이라고 한다면, 이 샘플의 평균이 198-202 범위에서 발견되지 않았으므로, 우리는 첫째
- 이 샘플이 우리가 포기하기로 한 5%의 범위안에 드는 샘플일 수 있다 (가능성은 5%이기는 하지만)
- 만약에 위의 가정을 무시할 수 있다면 (5%의 가정이므로), 감자의 납품자가 않좋은 감자를 납품하고 있다.
- 이 샘플이 우리가 포기하기로 한 5%의 범위안에 드는 샘플일 수 있다 (가능성은 5%이기는 하지만)
1.2. 모집단의 평균만을 알고 있을 경우 ¶
새들이 눈을 무서워할까? 만약에 무서워한다면, 여름에 농작물에서 새를 쫒는데 사용할 수 있을것이다. 연구자 B는 이를 가설로 세우고 테스트해보기로 하였다. B는 이를 위해서 실험환경을 우선 만들었다. 커다란 직사각형의 방의 한 면에는 사람의 눈을 그려 두고 이 주변에 새들이 쉴곳을 마련해 두었다. 반대편은 아무 표시가 없으며 주변에 쉴 곳을 마련해 두었다. B는 이제 16마리의 참새들을 구하여 각각의 새가 한 시간 동안 표시없는 벽에 얼마나 머물렀는가를 측정하였다.
측정한 결과, B는 다음과 같은 statistics를 얻었다.
- T distribution을 살펴본 결과,
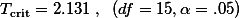 이라는 것을 알아내었다. 이 숫자를 기록해 둔다.
이라는 것을 알아내었다. 이 숫자를 기록해 둔다.
 이라고 가정한다 (null hypothesis).
이라고 가정한다 (null hypothesis). 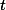 값을 구하여,
값을 구하여,  값과 비교하여 본다.
값과 비교하여 본다.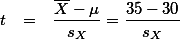
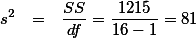
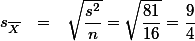
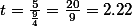 이다. z-test에서 언급한 것처럼, t 점수를 적용한다고 하면, 2보다 크므로, 영가설을 부정할 수 있다. 그러나, B는 z-test에서와 같이 population의
이다. z-test에서 언급한 것처럼, t 점수를 적용한다고 하면, 2보다 크므로, 영가설을 부정할 수 있다. 그러나, B는 z-test에서와 같이 population의  를 사용하지 않았으므로, t값으로 얻은 결과를 z값처럼 사용할 수 없다. T distribtuion table은 이렇게 불완전한
를 사용하지 않았으므로, t값으로 얻은 결과를 z값처럼 사용할 수 없다. T distribtuion table은 이렇게 불완전한 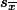 의 값을 염두에 두고 만들어진 것이다. 따라서 위에서 구한
의 값을 염두에 두고 만들어진 것이다. 따라서 위에서 구한  의 값은 z-test에서의 2 처럼 사용될 수 있다. 이 둘을 비교하면, 계산된 t 값이 더 크므로, 영가설을 부정하고, 따라서 연구가설을 채택한다. 단, B의 이 채택이 100% 옳은 결정이 아니라, 5%의 오류 가능성을 포함하고 있는 것이다.
의 값은 z-test에서의 2 처럼 사용될 수 있다. 이 둘을 비교하면, 계산된 t 값이 더 크므로, 영가설을 부정하고, 따라서 연구가설을 채택한다. 단, B의 이 채택이 100% 옳은 결정이 아니라, 5%의 오류 가능성을 포함하고 있는 것이다. B는 이와 같은 실험결과를 보고서의 형태로 기술한다.
참새들이 민짜 벽에 머문 평균시간은 35분이었다 (SD = 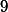 ). 실험 결과에서 얻어진 이 값은 눈의 영향력이 없다고 가정했을 때, 새들이 머물것으로 추정되는 30분과 통계적으로 유의미하게 다르다는 것이 밝혀졌다. 즉, 눈은 새들에게 영향력을 미친다고 판단되었다 (t(15) = 2.22, p < .05).
). 실험 결과에서 얻어진 이 값은 눈의 영향력이 없다고 가정했을 때, 새들이 머물것으로 추정되는 30분과 통계적으로 유의미하게 다르다는 것이 밝혀졌다. 즉, 눈은 새들에게 영향력을 미친다고 판단되었다 (t(15) = 2.22, p < .05).
1.3. 두 집단 간의 평균과 표준편차만으로 판단하는 경우 ¶
Independent t-test 문서는 미국의 대학생을 위해서 쓰여진 것이다. 우선 이것을 읽어 볼 것.
이 문서에서는 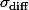 에 대해서는 언급을 하지 않았다. 약간 복잡하기 때문이었는데, 이전의 standard error 개념을 잘 이해했다면 실제로 계산법을 익혀볼 필요는 없다고 하겠다. 그러나, 실제로 구해보면 아래와 같이 구할 수 있다.
에 대해서는 언급을 하지 않았다. 약간 복잡하기 때문이었는데, 이전의 standard error 개념을 잘 이해했다면 실제로 계산법을 익혀볼 필요는 없다고 하겠다. 그러나, 실제로 구해보면 아래와 같이 구할 수 있다.
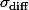 에 대해서는 언급을 하지 않았다. 약간 복잡하기 때문이었는데, 이전의 standard error 개념을 잘 이해했다면 실제로 계산법을 익혀볼 필요는 없다고 하겠다. 그러나, 실제로 구해보면 아래와 같이 구할 수 있다.
에 대해서는 언급을 하지 않았다. 약간 복잡하기 때문이었는데, 이전의 standard error 개념을 잘 이해했다면 실제로 계산법을 익혀볼 필요는 없다고 하겠다. 그러나, 실제로 구해보면 아래와 같이 구할 수 있다. 우선 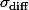 는 standard error of the sample means differences 라고 이야기 할 수 있다. Standard deviation of sampling distribution (즉, standard error) 은 하나의 집단만을 가지고 가상으로 여러 번 샘플을 뽑는 것을 가정하지만, 여기서는 두 집단 간의 평균차이로 만들어진 데이터의 분포곡선을 가정한다. 즉, 집단과 집단의 평균을 구한뒤 그 차이를 계속 기록함으로써 구하는 distribution 곡선을 상상한다.
는 standard error of the sample means differences 라고 이야기 할 수 있다. Standard deviation of sampling distribution (즉, standard error) 은 하나의 집단만을 가지고 가상으로 여러 번 샘플을 뽑는 것을 가정하지만, 여기서는 두 집단 간의 평균차이로 만들어진 데이터의 분포곡선을 가정한다. 즉, 집단과 집단의 평균을 구한뒤 그 차이를 계속 기록함으로써 구하는 distribution 곡선을 상상한다.
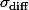 는 standard error of the sample means differences 라고 이야기 할 수 있다. Standard deviation of sampling distribution (즉, standard error) 은 하나의 집단만을 가지고 가상으로 여러 번 샘플을 뽑는 것을 가정하지만, 여기서는 두 집단 간의 평균차이로 만들어진 데이터의 분포곡선을 가정한다. 즉, 집단과 집단의 평균을 구한뒤 그 차이를 계속 기록함으로써 구하는 distribution 곡선을 상상한다.
는 standard error of the sample means differences 라고 이야기 할 수 있다. Standard deviation of sampling distribution (즉, standard error) 은 하나의 집단만을 가지고 가상으로 여러 번 샘플을 뽑는 것을 가정하지만, 여기서는 두 집단 간의 평균차이로 만들어진 데이터의 분포곡선을 가정한다. 즉, 집단과 집단의 평균을 구한뒤 그 차이를 계속 기록함으로써 구하는 distribution 곡선을 상상한다. | Data Table | ||
 | 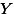 |  |
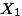 | 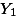 |  |
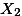 | 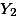 |  |
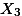 | 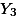 |  |
| . . . | . . . | . . . |
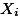 | 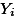 |  |
위의 예에서 만약에 X집단과 Y집단의 평균이 같다고 가정한다면, 어떤 종류의
 distribution 곡선이 나올까? 평균을 0으로 하며, 두 집단의 Variance를 더한 값 만큼의 Variance값을 갖는 곡선이 나올 것이라는 예상을 할 수 있다.
distribution 곡선이 나올까? 평균을 0으로 하며, 두 집단의 Variance를 더한 값 만큼의 Variance값을 갖는 곡선이 나올 것이라는 예상을 할 수 있다. 과연, 이와 같은 상황에서의 t값은 아래와 같이 구한다.
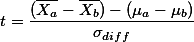
참조: One sample일때의 t 계산법:
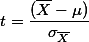
만약에 A그룹과 B그룹 간의 전체 모집단의 평균이 같다고 가정한다면 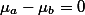 이 될것이다. 그리고 ,
이 될것이다. 그리고 , 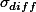 라는 기호는 두 집단의 모집단 표준편차를 안다고 가정할 때만 사용할 수 있으므로,
라는 기호는 두 집단의 모집단 표준편차를 안다고 가정할 때만 사용할 수 있으므로, 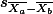 라고 표현할 수 있다.
라고 표현할 수 있다.
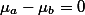 이 될것이다. 그리고 ,
이 될것이다. 그리고 , 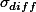 라는 기호는 두 집단의 모집단 표준편차를 안다고 가정할 때만 사용할 수 있으므로,
라는 기호는 두 집단의 모집단 표준편차를 안다고 가정할 때만 사용할 수 있으므로, 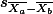 라고 표현할 수 있다.
라고 표현할 수 있다.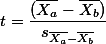
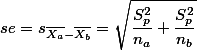
이때 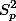 는 두 집단의 분산을 묶어서 구한 전체 분산값이다. 이 묶은 분산값은 아래와 같이 구한다.
는 두 집단의 분산을 묶어서 구한 전체 분산값이다. 이 묶은 분산값은 아래와 같이 구한다.
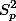 는 두 집단의 분산을 묶어서 구한 전체 분산값이다. 이 묶은 분산값은 아래와 같이 구한다.
는 두 집단의 분산을 묶어서 구한 전체 분산값이다. 이 묶은 분산값은 아래와 같이 구한다.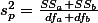
위의 식은 보기에는 복잡해 보이지만, 이전에 분산값과 standard error값을 구하는 공식을 떠 올리면 두 계산이 크게 다르지 않음을 알 수 있다.
참고:  ,
, 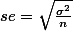
다른 예,
 |  |  |
| 1 | 1 | 11.4 |
| 2 | 1 | 11 |
| 3 | 1 | 5.5 |
| 4 | 1 | 9.4 |
| 5 | 1 | 13.6 |
| 6 | 1 | -2.9 |
| 7 | 1 | -0.1 |
| 8 | 1 | 7.4 |
| 9 | 1 | 21.5 |
| 10 | 1 | -5.3 |
| 11 | 1 | -3.8 |
| 12 | 1 | 13.4 |
| 13 | 1 | 13.1 |
| 14 | 1 | 9 |
| 15 | 1 | 3.9 |
| 16 | 1 | 5.7 |
| 17 | 1 | 10.7 |
| 18 | 2 | -0.5 |
| 19 | 2 | -0.93 |
| 20 | 2 | -5.4 |
| 21 | 2 | 12.3 |
| 22 | 2 | 2 |
| 23 | 2 | -10.2 |
| 24 | 2 | -12.2 |
| 25 | 2 | 11.6 |
| 26 | 2 | -7.1 |
| 27 | 2 | 6.2 |
| 28 | 2 | -0.2 |
| 29 | 2 | -9.2 |
| 30 | 2 | 8.3 |
| 31 | 2 | 3.3 |
| 32 | 2 | 11.3 |
| 33 | 2 | 0 |
| 34 | 2 | -1 |
| 35 | 2 | -10.6 |
| 36 | 2 | -4.6 |
| 37 | 2 | -6.7 |
| 38 | 2 | 2.8 |
| 39 | 2 | 0.3 |
| 40 | 2 | 1.8 |
| 41 | 2 | 3.7 |
| 42 | 2 | 15.9 |
| 43 | 2 | -10.2 |
1.3.1. 예 ¶
예를 들어보자.
C는 이미지를 연상하는 기억방법이 단순한 기억방법보다 효과가 크다고 생각한다. 이를 검증하기 위해서 C는 두 집단(각각의 n=10)을 샘플로 선정하여 아래의 Sample Statistics 를 얻었다.
| Group a | Group b |
 |  |
 |  |
 |  |
우선 연구가설과 영가설은:
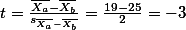
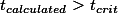 이므로, 영가설을 부정한다. 즉, 이 두 집단의 평균차이는 (-6)은 두 집단이 대동소이한 집단이라고 가정할 때, 즉 동일한 population을 가진 집단이라고 가정했을때에 나올 수 있는 차이를 훨씬 넘어선다.
이므로, 영가설을 부정한다. 즉, 이 두 집단의 평균차이는 (-6)은 두 집단이 대동소이한 집단이라고 가정할 때, 즉 동일한 population을 가진 집단이라고 가정했을때에 나올 수 있는 차이를 훨씬 넘어선다.
정신적인 이미지를 사용하여 기억을 한 그룹 (treatment group) 과 일반 그룹 (control group) 간의 기억력은 차이가 있는 것으로 나타났다 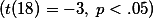 .
.
1.4. 동일집단 간의 차이에 대해서 알아볼 때 ¶
Eating disorder treatment. Was the treatment effective?
in Chapter 13.2 Table 13.1
| 17 | 87.3 | 98 | 10.7 |
in Chapter 13.2 Table 13.1
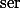 | 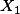 | 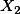 |  |
| 1 | 83.8 | 95.2 | 11.4 |
| 2 | 83.3 | 94.3 | 11 |
| 3 | 86 | 91.5 | 5.5 |
| 4 | 82.5 | 91.9 | 9.4 |
| 5 | 86.7 | 100.3 | 13.6 |
| 6 | 79.6 | 76.7 | -2.9 |
| 7 | 76.9 | 76.8 | -0.1 |
| 8 | 94.2 | 101.6 | 7.4 |
| 9 | 73.4 | 94.9 | 21.5 |
| 10 | 80.5 | 75.2 | -5.3 |
| 11 | 81.6 | 77.8 | -3.8 |
| 12 | 82.1 | 95.5 | 13.4 |
| 13 | 77.6 | 90.7 | 13.1 |
| 14 | 83.5 | 92.5 | 9 |
| 15 | 89.9 | 93.8 | 3.9 |
| 16 | 86 | 91.7 | 5.7 |
| mean | 83.22941176 | 90.49411765 | 7.264705882 |
| std | 5.016692724 | 8.475071577 | 7.157421077 |
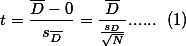
According to (1), 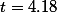 . Then what is the value of
. Then what is the value of 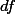 (case number-1)? = (16-1) = 15.
(case number-1)? = (16-1) = 15.
When critical value = .05,
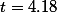 . Then what is the value of
. Then what is the value of 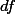 (case number-1)? = (16-1) = 15.
(case number-1)? = (16-1) = 15.When critical value = .05,

1.5. 가설테스트, 예 ¶
위의 감자의 QC의 예를 연구가설을 테스트하는 형식으로 익혀 두는 방법.
위에서 살펴본 것과 같이, 감자의 단위당 무게가 평균 200g이고 표준편차가 20이라고 주장하는 납품업자로부터 감자의 quality가 보고와 일치하는 지 궁금하여 샘플 (n=400)을 뽑아 확인하는 경우를 예로 들어 가설검증의 순서를 이야기 해 보겠다.
위에서 살펴본 것과 같이, 감자의 단위당 무게가 평균 200g이고 표준편차가 20이라고 주장하는 납품업자로부터 감자의 quality가 보고와 일치하는 지 궁금하여 샘플 (n=400)을 뽑아 확인하는 경우를 예로 들어 가설검증의 순서를 이야기 해 보겠다.
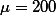 ,
, 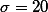
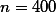 의 샘플을 뽑기로 하고, 이 샘플에 근거한 판단의 기준으로 .05 을 설정한다 (Type I error 참조). 이는 A가 자신의 가설검증 판단을 위해서 95%의 confidence interval 을 갖는다고 결정한다는 것을 의미한다.
의 샘플을 뽑기로 하고, 이 샘플에 근거한 판단의 기준으로 .05 을 설정한다 (Type I error 참조). 이는 A가 자신의 가설검증 판단을 위해서 95%의 confidence interval 을 갖는다고 결정한다는 것을 의미한다.- 이에 따라서 A는 Sampling을 통해서 sample을 뽑는다. 이렇게 뽑은 샘플의 평균이 396g 이었다. 즉,
 .
.
 값 (396)이 C사가 주장하는 400g과 일치하는지에 관심을 갖는 것이다 (위의 H1 참조). 이를 좀 더 설명하자면, A는 400개의 샘플을 뽑을 때 C사의 주장이 진실이라고 할지라도,그 평균이 정확히 C사가 주장하는 400g이 나오지는 않을 것이라는 것을 알고 있다. A는 자신이 막 뽑은 샘플의 평균이 전체 평균 400g의 모집단에서 n=400의 샘플을 뽑을 때 자연스럽게 나올 수 있는 평균인지를 알고 싶은 것이다. A는 이 시점에서 자신이 뽑은 샘플을 직접 다루는 것 보다는
값 (396)이 C사가 주장하는 400g과 일치하는지에 관심을 갖는 것이다 (위의 H1 참조). 이를 좀 더 설명하자면, A는 400개의 샘플을 뽑을 때 C사의 주장이 진실이라고 할지라도,그 평균이 정확히 C사가 주장하는 400g이 나오지는 않을 것이라는 것을 알고 있다. A는 자신이 막 뽑은 샘플의 평균이 전체 평균 400g의 모집단에서 n=400의 샘플을 뽑을 때 자연스럽게 나올 수 있는 평균인지를 알고 싶은 것이다. A는 이 시점에서 자신이 뽑은 샘플을 직접 다루는 것 보다는 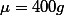 인 모집단을 가정한다면 (즉, C사의 주장이 진실이라면), n=400의 샘플의 평균이 개략적으로 어떤 범위에서 나와야 하는가를 알아보는 것이 더 좋은 방법이라고 생각한다. 이를 다시 이야기하면,
인 모집단을 가정한다면 (즉, C사의 주장이 진실이라면), n=400의 샘플의 평균이 개략적으로 어떤 범위에서 나와야 하는가를 알아보는 것이 더 좋은 방법이라고 생각한다. 이를 다시 이야기하면, 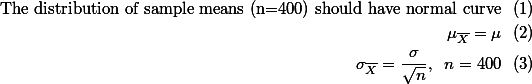
위의 정리는 central limit theorem 이라고 언급하였다. 이를 바탕으로 해서 n=400인 sampling distribution 의 성질을 정리하면  이다. 우리는 이를 standard error라고 부른다고 하였다.
이다. 우리는 이를 standard error라고 부른다고 하였다.
 이다. 우리는 이를 standard error라고 부른다고 하였다.
이다. 우리는 이를 standard error라고 부른다고 하였다. - 위의 정보(se)는
- 샘플의 숫자(n)가 400인 샘플을 뽑았을 때,
- 그 샘플의 평균값이 나타날 수 있는 범위를 정해주는 단위
- se = 1 이므로
- 샘플의 숫자(n)가 400인 샘플을 뽑았을 때,
- 400개의 샘플을 뽑았을 때, 그 샘플의 평균은 100이면 95번은 평균 200g을 기준으로 좌우로 2단위의 se만큼 떨어진 범위에서 발견될 것이다.
- se의 두 단위를 사용하였으므로, 좌우 범위는 각각 2이다.
- 즉, 398g - 402g에서 샘플의 평균이 나올 것이다.
- 마지막으로 이 범위에서 샘플의 평균이 발견될 확률은 95% 이다. 이유는 stadnard deviation of sample means = standard error = se 를 2 단위 썻기 때문이다.
- 즉, 우리는 400개의 샘플을 뽑았을 때, 그 샘플의 평균이 398에서 402일 거라는 확신을 95%하게됨.
- 이 샘플이 우리가 포기하기로 한 5%의 범위안에 드는 샘플일 수 있다 (가능성은 5%이기는 하지만)
- 만약에 위의 가정을 무시할 수 있다면 (5%의 가정이므로), C사가 좋지 않은 감자를 납품하고 있다.
1.6. 가설테스트 요약 ¶
1. 연구가설을 세운다
2. 샘플을 취한다. 이 때 샘플의 규모, n과 허용오차 (.05)를 정한다.
3. 연구가설을 뒤집어 영가설을 만든다.
4. 이를 근거로 검증절차를 따른다.
5. 절차의 결과를 가지고 영가설을 부정할지, 채택할지 결정한다.
6. 위에 따라, 연구가설에 대한 판단을 한다.
2. 샘플을 취한다. 이 때 샘플의 규모, n과 허용오차 (.05)를 정한다.
3. 연구가설을 뒤집어 영가설을 만든다.
4. 이를 근거로 검증절차를 따른다.
5. 절차의 결과를 가지고 영가설을 부정할지, 채택할지 결정한다.
6. 위에 따라, 연구가설에 대한 판단을 한다.
1.7. Example ¶
Use the file (the above)
gender: gender
TmobConv: time spent in mobile conversation
mobout: number of mobile out-calls
mobin: number of mobile in-calls
mobpeople: number of people, communicating with via mobile phone
Make three hypotheses:TmobConv: time spent in mobile conversation
mobout: number of mobile out-calls
mobin: number of mobile in-calls
mobpeople: number of people, communicating with via mobile phone
1.8. T-TEST in English ¶
Included section (from Independent t-test)
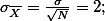
Also we know that the mean of (the samples means) is the same as the population mean. That is,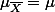 .
.
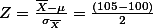 .
.
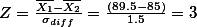 .
.
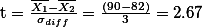 .
.
 .
.
T-TEST ¶
I have thought a proper way to make the t-test accessible; but, I figured out that it is not helpful to skip z-score and z-test. Before I tell any further, I'd like to mention that the t-test and z-test are virtually the same. Some differences are discussed later.
I will talk about z-test first.
I am repeating things because statistics tend to confuse us. So, let's start with standard error.
Do you remember the concept of the standard error of the mean? I have told several times that it is important -- it pops out here. The standard error of the mean refers to the standard deviation of the means of (many imaginary) samples from a particular population you are interested in.
The concept, the standard error of the mean gives the "possible range of mean scores" of samples (given a size of N) from a population. After you figure out the range of possible mean scores, you can estimate the mean score of the population. For example, in the IQ score test, suppose it is known that the national IQ score average is 100 (from the reliable statistical source) and the standard deviation is 10. With this information, you can calculate the standard error of the means with the formula (see the figure for the formula). Since the formula wants you to provide the number of the sample (sample size), you decided that you will take 25 individuals for a sample. Then, the standard error of the means of IQ score test, with the sample size 25, would be 2.
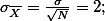
Also we know that the mean of (the samples means) is the same as the population mean. That is,
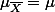 .
.Because the standard error is actually the standard deviation of sample means, we can use the 68-95-99 rule here to estimate the range of the possible population mean.
1 standard error unit: 1*se = 2 2 standard error units: 2*se = 4 3 standard error units: 3*se = 6 Mean +- 1*se = 100 +- 1(2) = 98 - 102 with 68% confidence; Mean +- 2*se = 100 +- 2(2) = 96 - 104 with 95% confidence; Mean +- 3*se = 100 +- 3(2) = 94 - 106 with 99% confidence
What it tells is that if we take a random sample (not imaginary, n=25), the mean should be found in the above ranges. With 68% sure, the mean of the sample would lie between 98 to 102. With 95% sure, the mean of the sample would lie between 96-104. With 99% sure, the mean of the sample would be found between 94-106.
Now, suppose that you took a sample (n=25) and found that the mean score for this sample was 105. From this number, you can immediately assume that there is something wrong. That is, with 95% confidence, the means of samples (n=25) should fall between the 96 and 104. But, the mean of this particular sample is 105. So, we may think that this particular sample is unusual in comparison to the characteristic of the population. Or, we can think another way around -- what we were told as national average IQ score (=100) may be wrong.
Stop here. This is a recap for the concept of the standard error of the means.
In the above, we figured out the ranges first, got the mean of a sample; and compare it to the ranges. We can simplify these by using z-score. In other words, we can regard the numerical value of one standard error as one unit. In this case, because the standard error is 2, one unit of standard error is 2. How far the mean of the particular sample (mean = 105) was off from the mean of the population in the above example? -- 5 (105 (mean of the sample) - 100 (mean of the population)). Numerically it is off by 5. Now, how many standard error units is this mean (105) off from the mean of the population? Since we regard numerical value 2 as one unit of standard error, it is 2.5 units off from the population (5 divided by the unit of standard error, 2). This sounds complex. But, if we see the mathematical form below:
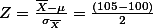 .
.As we figured out the result is 2.5. This value is called z-value (usually z means standardized). If you take a look at the below:
1 standard error unit: 1*se = 2 -- 68% -- z-score = 1 2 standard error units: 2*se = 4 -- 95% -- z-score = 2 3 standard error units: 3*se = 6 -- 99% -- z-score = 3In stead of dealing with 2, 4, and 6 which are numerical, now we can use 1, 2, and 3 to compare. In the example, we got 2.5 (z-score) which is bigger than the underlined 2. Therefore, we can see that the mean of the sample (105) falls out of the range provided with 95% certainty (2 standard error unit). Therefore, we can reach the same conclusion as we did. That is, we may say that, with 95% certainty, this particular sample seems an unusual case considering the given characteristic of the population. Or, we can think another way around -- what we were told as national average IQ score (=100) may be wrong with 95% certainty.
The benefit of using z-score is that now we can compare the obtained value for our sample to the number 2 (if you are required to employ 95% certainty. If you are required to employ 68% certainty, you can use the number 1, right?). This is because we "unit-ized" or "standardized" the score. This was obtained through just dividing the difference (between mean of the sample and the mean of the population) with the standard error of the means.
There is another application of this kind of test. In the above example, we just had one sample and were given the parameters for the population (do you remember the terms, parameter and population?). Suppose that we have two samples, instead of one. And we want to see whether two samples are the same kinds. For example, one sample is students who do not use the class web site. And the other is those who use the class site as a study resource. We got the exam result and want to compare them to see (judge, or decide) whether they are different. This is called two-sample z-test.
For this particular test, we use the standard error of the differences of the means. This is a different kind of standard error. Do you remember that I told you that there are many kinds of standard errors? -- the standard error of the probabilities, the standard error of the means, standard error of the differences of the means, etc. There are many others. All stem from the same idea, though. For this term, the standard error of the differences of the means, we do the same imaginary experiment. We take a sample from each group (or population); get the mean of the each sample; compare them (by subtracting one mean from the other); record the difference (compared result); take another sample from each group (or population); get the sample means; compare them; record the difference; ..... You keep doing it and get the statistics out of the record. The standard deviation obtained from this record has the exact same characteristics as the standard error of the means. And this is called the standard error of the differences of the means.
Let's go back to the example. We have 89.5 and 85 as the mean of the each sample -- those who use the class web site and those who do not. Suppose that we got the standard error of the differences of the means (1.5). We can use the same procedure as the above (with some modification: we now subtract one mean from the other)
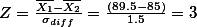 .
.Here, since we have the z-value, 3, which is bigger than 2 (assumed that 95% certainty was employed), we can argue that with 95% certainty, the two sample are different from each other in terms of the performance on the exam.
What can we say about this? We can say that those who use the class web site regularly tends to have higher exam scores in comparison to those not. The difference found in the above samples turned out to be statistically significant. That is, the differences was not due to a mere chance.
Now, about t-test (you have been waiting too long).
But, there is nothing much to say about because it is the almost same thing as the Z-test. Some points that I want to make though are
- that you need to refer to t-distribution table to make the statistical decision (rejecting the null hypothesis, p. 399 in the textbook.); As we discussed, the t-test (z-test) score uses the concept of standard error of mean differences (between two groups). So, our common sense (if it works ok) tells us, "Hey, if the mean difference between two groups are relatively small, the test score will be small. In fact, if they are identical, the test score should be 0 (zero)." So, when you look up the t-test table with your "calculated t-test score (value)", your calculated score should be bigger than the critical score (value) in order to say that there IS difference between the two groups.
- that the T-test is used with small sample sizes;
- the T-test is mostly used with two-sample problems (two-sample t-test; same thing as two-sample z-test).
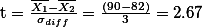 .
.You also need to figure out what is the degree of the freedom. The formula for this is:
 .
.If we take a look at the t-distribution table:
the critical value: 2.074 at 0.05 probability level (p = 0.05). the critical value: 2.819 at 0.01 probability level (p = 0.001).
Now you need to compare the calculated t-test value (2.67) and the critical value found in the table (2.074 at p = 0.05 level and 2.819 at p = 0.001 level). You figure out that the t-test value is bigger than the critical value at 0.05 level. You know that the t-test value depends upon the value of the difference between bar(X_1) text(and) bar(X_2) (see the above formula) -- if the difference is big the t-test value gets big. If there were no difference between the two groups in the first place, the t-test value is going to be zero (0). So, if obtained t-test value is larger than the critical value, you can say that there seems real difference in exam score between the two groups with 95% confidence. But, it is not the case at the 0.01 level. The obtained t-test value is smaller than the critical value at 0.01 level. Therefore, you cannot say that there seems real difference in the exam score between the two groups with 99% confidence.
2. External Links ¶
![[http]](http://wiki.commres.org/imgs/http.png) Hypothesis Testing:(http://www.uwsp.edu/psych/stat/10/hyptestc.htm) Continuous Variables (1 Sample)
Hypothesis Testing:(http://www.uwsp.edu/psych/stat/10/hyptestc.htm) Continuous Variables (1 Sample)
![[http]](http://wiki.commres.org/imgs/http.png) Hypothesis Testing:(http://www.uwsp.edu/psych/stat/11/hyptest2s.htm) Continuous Variables (2 Samples)
Hypothesis Testing:(http://www.uwsp.edu/psych/stat/11/hyptest2s.htm) Continuous Variables (2 Samples)