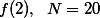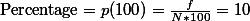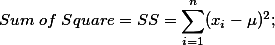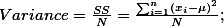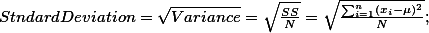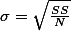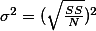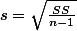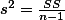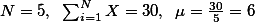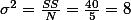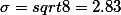Difference between r1.9 and the current
@@ -2,7 +2,7 @@
[[TableOfContents]]= Scores (기록) =
관찰(Observation)의 결과를 기록하는 방법::
||||<table class="wikiLeft"> $X$ ||
||||<table class="wikiCenter"> $X$ ||
||||37 ||||||35 ||
||||35 ||
@@ -11,7 +11,7 @@
||||17 ||||||16 ||
||<table class='wikiLeft'> $X$ || $Y$ ||
||<table class='wikiCenter'> $X$ || $Y$ ||
||72 ||165 ||||68 ||151 ||
||70 ||160 ||
@@ -20,8 +20,8 @@
||64 ||120 ||테이블에서 변인(변수)는 X로 표시되고, 이 변수에 관한 관찰의 기록을 해당 컬럼에 적는다. 가령, 첫 번째 사람의 시험점수가 37점이고, 두 번째 사람이, 35, 세번째 35, 네 번째 30, 등등이면, 위와 같이 기록한다. 만약에 observation이 2개 이상일 때에는 각 subject에 해당하는 기록을 같이 나열한다. 아래의 예는 변인 X 와 Y 에 해당하는 score를 각 subject에 맞게 표시한 것이다.
||<table class='wikiLeft'> SEX (Male=0, Female=1) ||
||<table class='wikiCenter'> SEX (Male=0, Female=1) ||
||1 ||||1 ||
||0 ||
@@ -30,14 +30,21 @@
||0 ||||1 ||
||0 ||
= Summation =
$\sum$ sign은 모든 score를 합한다는 것을 의미한다. $\sum_{i=1}^N X_i$ 는 변인 X이 가진 N개의 모든 score, $\{X_1, X_2, . . . . X_N\}$ 를 모두 더한다는 의미이다. 가령 $\{10, 6, 7, 4 \}$ 의 집합이 있을 때, $\sum_{i=1}^N X_i$ 의 값은 $27$ 이며, 샘플의 갯수는 $N = 4$ 이다. $\sum_{i=1}^N(X_i-1)^2$ 은 각 subject의 score에서 1을 뺀 후에, 그 숫자를 제곱한 숫자를 구하여, 이를 모두 더한다는 뜻이다.
$\sum$ sign은 모든 score를 합한다는 것을 의미한다. $ \displaystyle \sum_{i=1}^N X_i $ 는 변인 X이 가진 N개의 모든 score, $\{X_1, X_2, . . . . X_N\}$ 를 모두 더한다는 의미이다. 가령 $\{10, 6, 7, 4 \}$ 의 집합이 있을 때, $ \displaystyle \sum_{i=1}^N X_i $ 의 값은 $27$ 이며, 샘플의 갯수는 $N = 4$ 이다. $\displaystyle \sum_{i=1}^N(X_i-1)^2 $ 은 각 subject의 score에서 1을 뺀 후에, 그 숫자를 제곱한 숫자를 구하여, 이를 모두 더한다는 뜻이다.
== 예제 ==
$X = \{3, 1, 7, 4 \}$ 에서,
$ \textstyle\sum_{i=1}^N X_i \;,\;\; \textstyle\sum_{i=1}^N X^2 \;,\;\; \left[\textstyle\sum_{i=1}^N X_i\right]^2 $ 의 값을 각각 구하시오.
$ \displaystyle \sum_{i=1}^N X_i $
$ \displaystyle \sum_{i=1}^N X^2 $
$ \left[\displaystyle\sum_{i=1}^N X_i\right]^2 $
의 값을 각각 구하시오.
= Frequency =
{{{
@@ -83,6 +90,7 @@
||5||2||||6||1||
[[HTML(<div style='clear:both'> </div>)]]
attachment:histogram.png||<table class='wikiLeft'> $X$ || $f$ ||
@@ -90,6 +98,8 @@
||B||5||||C||20||
[[HTML(<div style='clear:both'> </div>)]]
Normal distribution
@@ -100,8 +110,8 @@
== Median ==[Median]
== Mode ==
Mode는 sample의 distribution에서 가장 빈도수가 높은 값을 말한다. 가령 아래와 같은 frequency table은 어느 식당에서 100명의 학생이 점심으로 먹은 메뉴이다:
||<table class='wikiLeft'>|| '''mode''' ||
Mode는 sample의 distribution에서 가장 빈도수가 높은 값을 말한다. 가령 아래와 같은 frequency table은 어느 식당에서 100명의 학생이 점심으로 먹은 메뉴이다: 이 때의 Mode 값은 빈도수(f)가 가장 높은 항목인 똑복이이다 (42라고 하지는 않는다).
||<table class='wikiCenter'>|| '''mode''' ||
|| Restaurant || f |||| 김밥 || 5 ||
|| 라면 || 16 ||
@@ -109,7 +119,6 @@
|| 탕수육 || 18 |||| 특별메뉴 || 7 ||
|| 오뎅 || 12 ||
아래는 시간대 별로 잡힌 물고기의 숫자를 표시한 것이다. 여기서 최대 빈도수를 가지는 값은 오전 6시의 값이고, 따라서 이 그래프의 mode는 6시이다. 하지만, mode는 상대적으로 높은 값을 갖는 범주를 모두 지칭하는 경우가 많으므로 여기서의 mode값은 오전 6시와 오후 6시라고 하는 것이 타당하다. 이렇게 두개의 mode를 가지는 distribution을 bi-modal한 distribution이라고 한다.
@@ -119,8 +128,6 @@
만약에 nominal한 데이터가 ratio한 변인의 값을 가질 때는 mode를 사용한다. 쉽게 이야기해서 아래와 같은 예이다. 여기서 모드값은 C이다.
[[Attachment(bar-graph.png, width=300,caption="bar graph",align=center)]]
== Skewed distribution ==
Skewness란 normal distribution이 아닌 distribution을 말할 때 쓰이는 개념이다.
@@ -134,21 +141,25 @@
= Variance, Standard Deviation =See also, [Variance] and [StandardDeviation]
$Sum \; of \; Square = SS = \displaystyle\sum_{i=1}^n (x_i-\mu)^2$ ;
$Variance = \frac{SS}{N}=\frac{\sum_{i=1}^n ({x_i - \mu})^2}{N} $ ;
$Stndard Deviation = \sqrt{Variance} = \sqrt{\frac{SS}{N}} = \sqrt{\frac{\sum_{i=1}^n ({x_i - \mu})^2}{N}} $ ;
$Sum \; of \; Square = SS = \displaystyle\sum_{i=1}^n (x_i-\mu)^2 ;$
$Variance = \frac{SS}{N}=\frac{\sum_{i=1}^n ({x_i - \mu})^2}{N} ; $
$Stndard Deviation = \sqrt{Variance} = \sqrt{\frac{SS}{N}} = \sqrt{\frac{\sum_{i=1}^n ({x_i - \mu})^2}{N}} ; $
== for Population ==For population standard deviation: $\sigma = \sqrt{\frac{SS}{N}}$
For population variance: $\sigma^2 = (\sqrt{\frac{SS}{N}})^2 $
== for sample ==For sample standard deviation -> $s = \sqrt{\frac{SS}{n-1}} $
For sample variance -> $s^2 = \frac{SS}{n-1} $
왜 n-1을 사용하는가?
[wiki:SamplingBias sampling bias]를 없애기 위해서
see [wiki:DegreesOfFreedom Degrees Of Freedom] 혹은 [wiki:DegreesOfFreedom 자유도]
== Degrees of Freedom == 자유도의 개념은 연구자가 샘플을 사용할 때, 각 샘플값이 변화(vary)할 수 있는 최대치의 샘플 숫자를 말한다. See also [DegreesOfFreedom]
가령, $n=3,\;\; \sum_{i=1}^n X_i = 30, \;\; \overline{X}=10$ 일때, 연구자는 3개의 샘플 구성원 중 두 개의 값을 알면, 나머지 하나의 값이 무엇인지 확인해 보지 않아도 알수 있다. 만약에 처음 두 숫자가 $X_1 = 0,\; X_2 = 5$ 인 것을 알고 있다면, 연구자는 마지막 한 샘플의 숫자가 $X_3 = 25$ 임을 알 수 있다. 즉, 처음 2개의 숫자를 제외한 마지막 숫자는 처음 두 숫자에 의해서 정해지게 되는데, 이렇게 변화할 수 있는 샘플 구성원의 숫자를 <b>자유도</b>라고 한다.
가령, $n=3,\;\; \sum_{i=1}^n X_i = 30, \;\; \overline{X}=10$ 일때, 연구자는 3개의 샘플 구성원 중 두 개의 값을 알면, 나머지 하나의 값이 무엇인지 확인해 보지 않아도 알수 있다. 만약에 처음 두 숫자가 $X_1 = 0,\; X_2 = 5$ 인 것을 알고 있다면, 연구자는 마지막 한 샘플의 숫자가 $X_3 = 25$ 임을 알 수 있다. 즉, 처음 2개의 숫자를 제외한 마지막 숫자는 처음 두 숫자에 의해서 정해지게 되는데, 이렇게 변화할 수 있는 샘플 구성원의 숫자를 '''자유도'''라고 한다.
자유도 (degress of freedom, df)은 아래와 같이 사용한다.
Contents
1. Scores (기록) ¶
관찰(Observation)의 결과를 기록하는 방법::
테이블에서 변인(변수)는 X로 표시되고, 이 변수에 관한 관찰의 기록을 해당 컬럼에 적는다. 가령, 첫 번째 사람의 시험점수가 37점이고, 두 번째 사람이, 35, 세번째 35, 네 번째 30, 등등이면, 위와 같이 기록한다. 만약에 observation이 2개 이상일 때에는 각 subject에 해당하는 기록을 같이 나열한다. 아래의 예는 변인 X 와 Y 에 해당하는 score를 각 subject에 맞게 표시한 것이다.
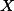 | |
| 37 | |
| 35 | |
| 35 | |
| 30 | |
| 25 | |
| 17 | |
| 16 |
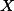 | 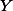 |
| 72 | 165 |
| 68 | 151 |
| 70 | 160 |
| 45 | 140 |
| 70 | 160 |
| 64 | 120 |
테이블에서 변인(변수)는 X로 표시되고, 이 변수에 관한 관찰의 기록을 해당 컬럼에 적는다. 가령, 첫 번째 사람의 시험점수가 37점이고, 두 번째 사람이, 35, 세번째 35, 네 번째 30, 등등이면, 위와 같이 기록한다. 만약에 observation이 2개 이상일 때에는 각 subject에 해당하는 기록을 같이 나열한다. 아래의 예는 변인 X 와 Y 에 해당하는 score를 각 subject에 맞게 표시한 것이다.
| SEX (Male=0, Female=1) |
| 1 |
| 1 |
| 0 |
| 1 |
| 0 |
| 0 |
| 1 |
| 0 |
변인이 Nominal인 경우에는 각각의 attribute에 대표값을 정하여 주고 이를 기록한다.
2. Summation ¶
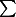 sign은 모든 score를 합한다는 것을 의미한다.
sign은 모든 score를 합한다는 것을 의미한다. 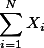 는 변인 X이 가진 N개의 모든 score,
는 변인 X이 가진 N개의 모든 score, 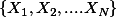 를 모두 더한다는 의미이다. 가령
를 모두 더한다는 의미이다. 가령 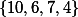 의 집합이 있을 때,
의 집합이 있을 때, 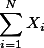 의 값은
의 값은 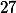 이며, 샘플의 갯수는
이며, 샘플의 갯수는  이다.
이다. 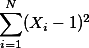 은 각 subject의 score에서 1을 뺀 후에, 그 숫자를 제곱한 숫자를 구하여, 이를 모두 더한다는 뜻이다.
은 각 subject의 score에서 1을 뺀 후에, 그 숫자를 제곱한 숫자를 구하여, 이를 모두 더한다는 뜻이다. 3. Frequency ¶
10점짜리 퀴즈 스코어
{8, 9, 8, 7, 10, 9, 6, 4, 9, 8, 7, 8, 10, 9, 8, 6, 9, 7, 8, 8}
N=20
위의 자료는 아래와 같은 형식으로 요약할 수 있다.
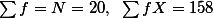
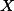 | 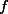 | 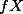 |
| 10 | 2 | 20 |
| 9 | 5 | 45 |
| 8 | 7 | 56 |
| 7 | 3 | 21 |
| 6 | 2 | 12 |
| 5 | 0 | 0 |
| 4 | 1 | 4 |
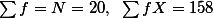
5. Frequency ¶
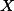 |
| 6 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 5 |
| 4 |
| 3 |
| 3 |
| 5 |
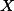 | 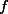 |
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 2 |
| 5 | 2 |
| 6 | 1 |
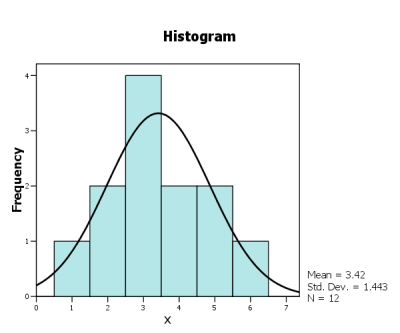
[PNG image (16.59 KB)]
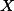 | 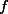 |
| A | 10 |
| B | 5 |
| C | 20 |
[PNG image (4.23 KB)]
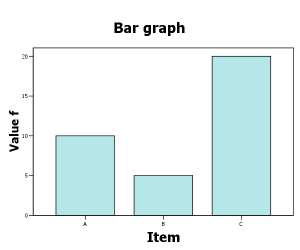
Normal distribution

[PNG image (32.01 KB)]
6.3. Mode ¶
Mode는 sample의 distribution에서 가장 빈도수가 높은 값을 말한다. 가령 아래와 같은 frequency table은 어느 식당에서 100명의 학생이 점심으로 먹은 메뉴이다: 이 때의 Mode 값은 빈도수(f)가 가장 높은 항목인 똑복이이다 (42라고 하지는 않는다).
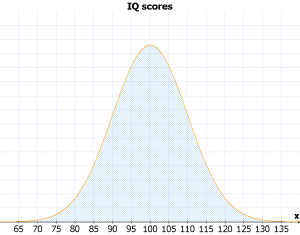
아래는 시간대 별로 잡힌 물고기의 숫자를 표시한 것이다. 여기서 최대 빈도수를 가지는 값은 오전 6시의 값이고, 따라서 이 그래프의 mode는 6시이다. 하지만, mode는 상대적으로 높은 값을 갖는 범주를 모두 지칭하는 경우가 많으므로 여기서의 mode값은 오전 6시와 오후 6시라고 하는 것이 타당하다. 이렇게 두개의 mode를 가지는 distribution을 bi-modal한 distribution이라고 한다.
| mode | |
| Restaurant | f |
| 김밥 | 5 |
| 라면 | 16 |
| 떡복이 | 42 |
| 탕수육 | 18 |
| 특별메뉴 | 7 |
| 오뎅 | 12 |
아래는 시간대 별로 잡힌 물고기의 숫자를 표시한 것이다. 여기서 최대 빈도수를 가지는 값은 오전 6시의 값이고, 따라서 이 그래프의 mode는 6시이다. 하지만, mode는 상대적으로 높은 값을 갖는 범주를 모두 지칭하는 경우가 많으므로 여기서의 mode값은 오전 6시와 오후 6시라고 하는 것이 타당하다. 이렇게 두개의 mode를 가지는 distribution을 bi-modal한 distribution이라고 한다.
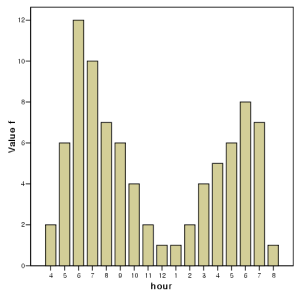
bi modal distribution [PNG image (7.03 KB)]
Mean, median, mode 세개의 값 중에서 어느 것을 취하는가의 문제: 앞에서도 이야기 하였지만, mean은 outlier 값에 상당한 영향을 받는다. Frequency 표에서 눈에 띄는 outlier가 존재한다면, Median값을 쓰는 것이 타당할 수도 있다. 혹은 outlier가 되는 값을 제외하고 mean값을 구하기도 한다.
만약에 nominal한 데이터가 ratio한 변인의 값을 가질 때는 mode를 사용한다. 쉽게 이야기해서 아래와 같은 예이다. 여기서 모드값은 C이다.


bar graph [PNG image (4.23 KB)]
6.4. Skewed distribution ¶
Skewness란 normal distribution이 아닌 distribution을 말할 때 쓰이는 개념이다.
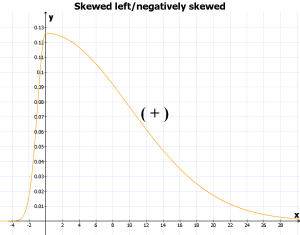
[PNG image (14.28 KB)]
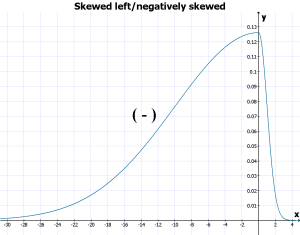
[PNG image (15.34 KB)]
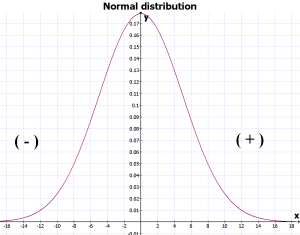
[PNG image (15.71 KB)]
7.3. Degrees of Freedom ¶
자유도의 개념은 연구자가 샘플을 사용할 때, 각 샘플값이 변화(vary)할 수 있는 최대치의 샘플 숫자를 말한다. See also DegreesOfFreedom
가령, 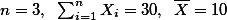 일때, 연구자는 3개의 샘플 구성원 중 두 개의 값을 알면, 나머지 하나의 값이 무엇인지 확인해 보지 않아도 알수 있다. 만약에 처음 두 숫자가
일때, 연구자는 3개의 샘플 구성원 중 두 개의 값을 알면, 나머지 하나의 값이 무엇인지 확인해 보지 않아도 알수 있다. 만약에 처음 두 숫자가 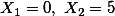 인 것을 알고 있다면, 연구자는 마지막 한 샘플의 숫자가
인 것을 알고 있다면, 연구자는 마지막 한 샘플의 숫자가  임을 알 수 있다. 즉, 처음 2개의 숫자를 제외한 마지막 숫자는 처음 두 숫자에 의해서 정해지게 되는데, 이렇게 변화할 수 있는 샘플 구성원의 숫자를 자유도라고 한다.
임을 알 수 있다. 즉, 처음 2개의 숫자를 제외한 마지막 숫자는 처음 두 숫자에 의해서 정해지게 되는데, 이렇게 변화할 수 있는 샘플 구성원의 숫자를 자유도라고 한다.
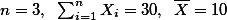 일때, 연구자는 3개의 샘플 구성원 중 두 개의 값을 알면, 나머지 하나의 값이 무엇인지 확인해 보지 않아도 알수 있다. 만약에 처음 두 숫자가
일때, 연구자는 3개의 샘플 구성원 중 두 개의 값을 알면, 나머지 하나의 값이 무엇인지 확인해 보지 않아도 알수 있다. 만약에 처음 두 숫자가 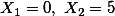 인 것을 알고 있다면, 연구자는 마지막 한 샘플의 숫자가
인 것을 알고 있다면, 연구자는 마지막 한 샘플의 숫자가  임을 알 수 있다. 즉, 처음 2개의 숫자를 제외한 마지막 숫자는 처음 두 숫자에 의해서 정해지게 되는데, 이렇게 변화할 수 있는 샘플 구성원의 숫자를 자유도라고 한다.
임을 알 수 있다. 즉, 처음 2개의 숫자를 제외한 마지막 숫자는 처음 두 숫자에 의해서 정해지게 되는데, 이렇게 변화할 수 있는 샘플 구성원의 숫자를 자유도라고 한다. 자유도 (degress of freedom, df)은 아래와 같이 사용한다.
Degrees of freedom,  샘플의 총 갯수
샘플의 총 갯수
 샘플의 총 갯수
샘플의 총 갯수여기서 사용된  은 위에서 사용된 sample의
은 위에서 사용된 sample의  와
와 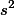 에서 사용된
에서 사용된  과 같다. 따라서, variance는 다음과 같이 나타낼 수 있다.
과 같다. 따라서, variance는 다음과 같이 나타낼 수 있다.
 은 위에서 사용된 sample의
은 위에서 사용된 sample의  와
와 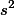 에서 사용된
에서 사용된  과 같다. 따라서, variance는 다음과 같이 나타낼 수 있다.
과 같다. 따라서, variance는 다음과 같이 나타낼 수 있다. 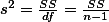
7.4. eg., ¶
- {1, 9, 5, 8, 7}의 distribution에서 mean, variance, standard deviation 값은?
| SS | ||
| X | 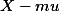 | (X-mu)^2 |
| 1 | -5 | 25 |
| 9 | +3 | 9 |
| 5 | -1 | 1 |
| 8 | +2 | 4 |
| 7 | +1 | 1 |
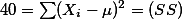 | ||
Q {10, 10, 10, 10, 10, 10}의 distribution에서 mean, variance, standard deviation 값은?
A
A
7.5. More about standard deviation and variance ¶
Standard deviation 과 variance 값이 의미하는 것은 모두 각개의 sample이 평균값으로 부터 얼마나 멀리 분포하는가에 관한 것이다 (영문 아티클 참조). 따라서,  이고
이고  의 분포를 갖는 sample이라는 단서로 연구자는 실제 개개의 sample이 어떻게 분포되어 있을 것인가를 알 수 있다. 이것은 거꾸로도 마찬가지이다. 연구자는 sample의 특성을 나타낼 때,
의 분포를 갖는 sample이라는 단서로 연구자는 실제 개개의 sample이 어떻게 분포되어 있을 것인가를 알 수 있다. 이것은 거꾸로도 마찬가지이다. 연구자는 sample의 특성을 나타낼 때,  값과
값과  값을 동시에 보여주는 것을 관례로 한다.
값을 동시에 보여주는 것을 관례로 한다.
 이고
이고  의 분포를 갖는 sample이라는 단서로 연구자는 실제 개개의 sample이 어떻게 분포되어 있을 것인가를 알 수 있다. 이것은 거꾸로도 마찬가지이다. 연구자는 sample의 특성을 나타낼 때,
의 분포를 갖는 sample이라는 단서로 연구자는 실제 개개의 sample이 어떻게 분포되어 있을 것인가를 알 수 있다. 이것은 거꾸로도 마찬가지이다. 연구자는 sample의 특성을 나타낼 때,  값과
값과  값을 동시에 보여주는 것을 관례로 한다.
값을 동시에 보여주는 것을 관례로 한다. 아래는 실제로 연구자가 보고를 할 때 사용하는 방식 중의 하나를 예로 나타낸다. 아래 표는 (1) 폭력적인 cartoon이 실험참가자들의 폭력적응대(aggresive responses)에 얼마나 영향을 미치는가를 알아내려는 실험이라는 것을 보여 주고; (2) 남자의 경우, 폭력적인 cartoon에 노출되었을 때 가장 폭력적이 된다른 것을 보아서, 폭력적인 cartoon이 폭력적인 응답을 부른다는 것을 나타내 준다. 단, 여기서, 첫 번째 cell의 SD값이 다른 SD값보다 높을 것을 보아서, cartoon의 영향력이 일괄적이지는 않다는 것 (SD, 즉, variance값이 크다는 것)은 폭력에 노출된 남자 참여자들의 폭력성의 값이 평균값인 15.72 주위에 잘 모여 있지 않다는 것을 나타내 준다. 따라서 연구자는, 남자들에게 폭력적인 cartoon이 영향을 미치기는 하지만, 그 효과가 일반적이지는 않고 개인마다 차이가 많다는 해석을 할 수 있다.
| Type of cartoon | ||
| Violent | Control | |
| Male | M=15.72 | M=6.94 |
| SD=4.43 | SD=2.26 | |
| Female | M=3.47 | M=2.61 |
| SD=1.12 | SD=0.98 | |
아래의 예에서, standard deviation과 variance에 대한 이해가 충분하다면, 어떤 집단 (X 와 Y)의 해당값들이 더 큰가를 계산없이 알 수 있다.
| X | Y |
| 34 | 26 |
| 35 | 10 |
| 36 | 57 |
| 35 | 37 |
- mean = 40, standard deviation = 4 의 normal distribution graph
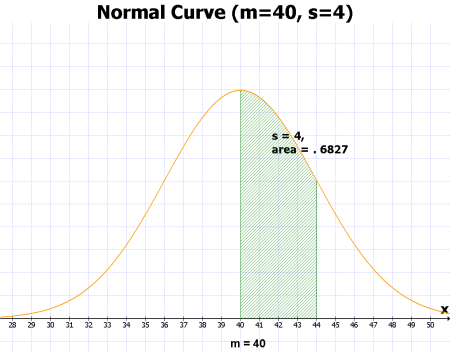 [PNG image (47.26 KB)]
[PNG image (47.26 KB)]
e.g., 아래를 샘플데이터라고 가정을 하고, deviation값들을 구하라.
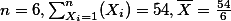
10, 7, 6, 10, 6, 15우선,
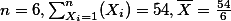
| X |  | 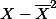 |
| 10 | 1 | 1 |
| 7 | -2 | 4 |
| 6 | -3 | 9 |
| 10 | 1 | 1 |
| 6 | 3 | 9 |
| 15 | 6 | 36 |
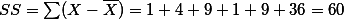

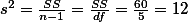
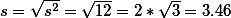



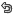




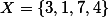 에서,
에서, 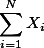
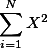
![$ \left[\displaystyle\sum_{i=1}^N X_i\right]^2 $ $ \left[\displaystyle\sum_{i=1}^N X_i\right]^2 $](/_cache/latex/2/26/9bd573f263f0a56880dafb28e22b71b0.png)