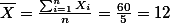WkPark/2202-01 › CalendarMacro/2201-02 › CalendarMacro/2201-09 › CalendarMacro/2199-04 › CalendarMacro/1829-08 › Mean
Difference between r1.2 and the current
@@ -4,7 +4,7 @@
= A simple explanation =기술통계 DescriptiveStatistics 혹은 추정통계 InferentialStatistics에서 가장 많이 쓰이는 Population이나 Sample의 중앙치를 나타내는 척도로서 다음과 같이 구한다.
$\mu = \displaystyle \frac{\sum_{\tiny{i=1}}^{\tiny{N}} \overline{X_i}}{N}$ .
$\mu = \displaystyle \frac{\displaystyle \sum_{\tiny{i=1}}^{\tiny{N}} {X_i}}{N}$ .
여기서 $\small\sum$ 기호는 시그마 Sigma라고 읽으며, 그리스어로 대문자 S를 뜻한다. 그 뜻은 해당 집합의 요소 (여기서는 $X_1, X_2, \;\dots\;$ )를 모두 더하는 것을 말한다. 따라서 위의 식은 $i=1$ 에서 $N$ 까지 갈 때 해당 $X_i$ 의 값을 모두 더한 후, 이 값을 $N$ 으로 나눈다는 것을 말한다. 흔히 $\mu = \tiny{\frac{\sum \overline{X_i}}{N}}$ 와 같이 해당 요소를 나타내는 $i$ 와 총 요소의 갯수를 나타내는 $N$ 기호를 생략하여 표기한다.
= More about Mean =
@@ -18,7 +18,7 @@
* 예, For a population of N = 4 scores, {3, 7, 4, 6}, the mean is: $\mu = \frac{\sum X_i}{N} = \frac{20}{4} = 5 $
평균값의 특성: 아래의 예에서 중요하게 보아야 할 점은 한 sample의 값이 다른 값들과는 다르게 훨씬 크거나 적을 경우에 이 값이 전체 평균에 미치는 영향이다. 이런 값을 가진 sample을 흔이 out-lier라고 하는데, outlier는 전체 평균에 상당한 영향을 미친다. 가령 첫 번째 예에서 평균은 6.00 이지만, 마지막 예는 12이다. 이렇게 평균값이 변한 이유는 sample 중 하나의 값이 1에서 31로 변했기 때문이다.
평균값의 특성: 아래의 예에서 중요하게 보아야 할 점은 한 sample의 값이 다른 값들과는 다르게 훨씬 크거나 적을 경우에 이 값이 전체 평균에 미치는 영향이다. 이런 값을 가진 sample을 흔이 [[HTML(<font color="red">outlier</font>)]] 라고 하는데, outlier는 전체 평균에 상당한 영향을 미친다. 가령 첫 번째 예에서 평균은 6.00 이지만, 마지막 예는 12이다. 이렇게 평균값이 변한 이유는 sample 중 하나의 값이 1에서 31로 변했기 때문이다.
* {9, 8, 7 ,5, 1}일때, $\overline{X} = \frac{\sum_{i=1}^n X_i}{n} = \frac{30}{5} = 6 $
* {9, 8, 7 ,5, 8}일때, $\overline{X} = \frac{\sum_{i=1}^n X_i}{n} = \frac{37}{5} = 7.40 $
1. A simple explanation ¶
기술통계 DescriptiveStatistics 혹은 추정통계 InferentialStatistics에서 가장 많이 쓰이는 Population이나 Sample의 중앙치를 나타내는 척도로서 다음과 같이 구한다.
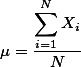 .
. 여기서 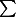 기호는 시그마 Sigma라고 읽으며, 그리스어로 대문자 S를 뜻한다. 그 뜻은 해당 집합의 요소 (여기서는
기호는 시그마 Sigma라고 읽으며, 그리스어로 대문자 S를 뜻한다. 그 뜻은 해당 집합의 요소 (여기서는 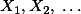 )를 모두 더하는 것을 말한다. 따라서 위의 식은
)를 모두 더하는 것을 말한다. 따라서 위의 식은  에서
에서 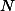 까지 갈 때 해당
까지 갈 때 해당 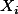 의 값을 모두 더한 후, 이 값을
의 값을 모두 더한 후, 이 값을 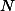 으로 나눈다는 것을 말한다. 흔히
으로 나눈다는 것을 말한다. 흔히 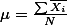 와 같이 해당 요소를 나타내는
와 같이 해당 요소를 나타내는 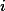 와 총 요소의 갯수를 나타내는
와 총 요소의 갯수를 나타내는 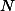 기호를 생략하여 표기한다.
기호를 생략하여 표기한다.
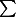 기호는 시그마 Sigma라고 읽으며, 그리스어로 대문자 S를 뜻한다. 그 뜻은 해당 집합의 요소 (여기서는
기호는 시그마 Sigma라고 읽으며, 그리스어로 대문자 S를 뜻한다. 그 뜻은 해당 집합의 요소 (여기서는 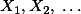 )를 모두 더하는 것을 말한다. 따라서 위의 식은
)를 모두 더하는 것을 말한다. 따라서 위의 식은  에서
에서 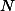 까지 갈 때 해당
까지 갈 때 해당 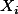 의 값을 모두 더한 후, 이 값을
의 값을 모두 더한 후, 이 값을 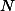 으로 나눈다는 것을 말한다. 흔히
으로 나눈다는 것을 말한다. 흔히 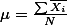 와 같이 해당 요소를 나타내는
와 같이 해당 요소를 나타내는 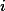 와 총 요소의 갯수를 나타내는
와 총 요소의 갯수를 나타내는 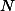 기호를 생략하여 표기한다.
기호를 생략하여 표기한다.2. More about Mean ¶
For population: 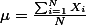
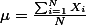
모집단(population)이라 함은 연구자가 관심을 가지는 집단 전체를 의미한다. 가령, 한 연구자가 대한민국 청소년의 인터넷 게임과 부모와의 관계에 대한 연구문제를 가지고 있다면, 이 연구자가 관심을 가지는 모집단은 대한민국의 청소년 이다. 청소년 (juvenile)을 어떻게 정하는가는 연구자의 관점에 따라서 약간 다를 수도 있겠지만, 기존의 권위적인 연구 혹은 지침서가 있다면, 그를 따르는게 보통일 것이다 (왜냐하면, 이렇게 동일 나이 집단을 연구함으로써, 서로간의 연구를 비교할 수도 있다). 복습을 하자면, 대한민국 청소년이라는 모집단에서 실제 서베이나 실험에 참가하는 집단을 선출하는 것을 sampling이라고 하고, 이렇게 해서 뽑혀진 혹은 선발된 참가자들을 sample이라고 한다. Sampling을 위해서는 대한민국 청소년, 즉 모집단을 나열한 리스트가 필요한데, 이 때 사용되는 리스트를 sampling frame이라고 한다. 가령, 문광부가 중고등학교 학생의 명단을 모두 보유하고 있고 연구자가 이를 사용한다고 하면, 중고등학교 학생의 명단이 바로 sampling frame이다.
For sample: 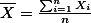
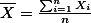
위에서 언급한것과 같이 sample은 모집단을 대표하는 명단(sampling frame)에서 추출된 개인들의 합을 말한다. 모집단 전체를 조사하는 경우는 드물기 때문에 (census의 경우를 제외하고는 거의 없다. 이런 모집단 전체를 조사하는 것을 enumeration이라고 한다), 연구자는 sample의 특성(성격)을 알아내고, 이를 바탕으로 수학적인 기법을 이용하여, 모집단의 성격을 추론한다.
- 예, For a population of N = 4 scores, {3, 7, 4, 6}, the mean is:
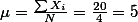
- {9, 8, 7 ,5, 1}일때,
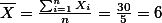
- {9, 8, 7 ,5, 8}일때,
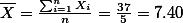
- {9, 8, 7 ,5, 31}일때,