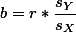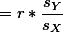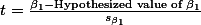FrontPage › Regression
Difference between r1.18 and the current
@@ -9,19 +9,20 @@
여기서, a는 절편이라고 (intercept) 하고, b는 기울기라고 (slope) 한다. 즉, 완벽한 상관관계일 때 나타나는 관계 그래프는 일차 방정식의 형태를 띄게 된다 (따라서 이를 linear한 관계라고 한다).
그리고 이렇게 해서 얻는 곡선을 회귀 곡선이라고 (regression line) 하며, 이 곡선을 표현하는 등식을 회귀방정식 (regression equation)이라고 한다. 실제에서는 r 값이 1 혹은 -1인 경우가 드물다. 이것이 의미하는 것은 데이터가 어느 일정한 방향성과 응집성을 가지고는 있으나, 이것이 완변한 선형을 이루지는 않는다는 것을 의미한다 (그림 참조). 이와 같은 데이터에도 회귀곡선을 그릴 수 있는데 (따라서 회귀식을 구할 수 있는데) 이 장에서는 이에 대해서 설명한다.
그리고 이렇게 해서 얻는 곡선을 회귀 곡선이라고 (regression line) 하며, 이 곡선을 표현하는 등식을 회귀방정식 (regression equation)이라고 한다. 실제에서는 r 값이 1 혹은 -1인 경우가 드물다. 이것이 의미하는 것은 데이터가 어느 일정한 방향성과 응집성을 가지고는 있으나, 이것이 완변한 선형을 이루지는 않는다는 것을 의미한다 (그림 참조). 이와 같은 데이터에도 회귀곡선을 그릴 수 있는데 (따라서 회귀식을 구할 수 있는데) 이 장에서는 이에 대해서 설명한다.
그림에서 보는 것처럼, 실제 데이터에서 얻게 되는 회귀 방정식은 정확한 데이터의 움직임을 나타내 줄 수는 없으므로 추정치를 표시하는 지표로 사용된다.
[[Attachment(r.RegressionLine2.png,width=350,align=left,caption="r=-+1이 아닌 회귀선과 데이터")]]
그림에서 보는 것처럼, 실제 데이터에서 얻게 되는 회귀 방정식은 정확한 데이터의 움직임을 나타내 줄 수는 없으므로 추정치를 표시하는 지표로 사용된다.
$\hat Y = a + bX $
위의 경우에는, $\hat Y = 5 + 2 X $
[[Attachment(r.RegressionLine3.png,width=350,align=left,caption="추정치와 관측치 간의 차이 = 오차")]]
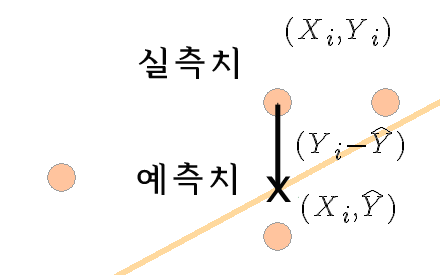
여기서 $\hat Y$ 는 $X_i$ 에서 실제 데이터 값을 ( $Y_i$ ) 추정해주는 값을 말하며 Y hat이라고 읽는다. 완벽한 correlatin이 아닐 경우에 $\hat Y$ 의 값은 실제 $Y_i$ 값과 다를 수 있다. 회귀식을 이용하여 구한 $\hat Y$ 값은 __기대치__ 혹은 __예측치__라고 할 수 있으며, 데이터를 이용하여 알아낸 $Y_i$ 값은 __관측치__ 혹은 __실측치__라고 할 수 있는데 이와 같이 실제 데이터의 '''관측치와 기대치와의 __차이__'''는 그림에서 괄호로 묶은 부분을 의미하며 이는 $(Y_i - \hat Y)$ 로 표현한다.
상관관계에서 살펴 본것처럼, 관측된 데이터는 최소자승 (Least Squared) 법을 이용하여 회귀식을 유도할 수 있는데, 이때의 절편과 기울기 값은 각각 다음과 같이 구할 수 있다:
@@ -29,6 +30,10 @@
$a = \displaystyle \overline{Y} - b \overline{X} $
http://vassarstats.net/textbook/f03x1b.gif
최소자승이 의미하는 것은 위의 그림과 같다. regression line (회귀선)으로 X 값에 해당하는 Y 값을 예측할 수 있는데, 이때에는 실측값과 차이가 날 수 있다. 이 차이가 위의 그림에서 녹색선인데, 이 녹색선의 합이 최소값을 갖도록하는 것을 최소자승(least squared)법이라고 한다.
[[HTML(<div style='clear:both'> </div>)]]
간혹, 다른 교재를 보면,
@@ -119,7 +124,7 @@
== 표준오차 잔여변량 (standard error, residual) ==아래 그림은 변인 X 와 Y 간의 관계를 (association) 나타내주는 그래프이다. 그리고, 이 그래프에서 $\overline{Y} = 30$ 이다. 이 데이터 중에서 X에 대한 정보가 없다고 가정하고, Y 관측치를 예측하려면 어떻게 해야 할까? 당연히 연구자는 자신이 가지고 있는 Y 변인 데이터의 중앙값인 평균 ( $\overline{Y}$ ) 을 사용하려고 할 것이다. 그러나, 연구자가 Y 변인의 평균값을 Y의 대표값이라고 하기에는 개인의 실제값 (혹은 관측치)과 평균값 간의 오차가 너무 크다. 이 오차를 줄이기 위해서 만들어진 것이 회귀선이다 (regression line, 오렌지 라인). 따라서 회귀선은 평균값만을 사용할 때 나타나는 오차를 줄여주는 역할을 한다. 이렇게 줄어든 오차를 '''설명된 오차'''라고 ('''explained error''') 한다. 예를 들면, 아래 그림에서 $X=15$ 일때의 Y 값의 하나인 $Y_i$ 값은 평균값인 $\overline{Y}$ 값에서 녹색선과 검은색 선의 길이만큼의 오차를 갖는다. 이렇게 된 이유는 연구자가 __오직__ Y 값만을 분석하여 Y 값을 예측했기 때문이다.
[[Attachment(r.Predicted.Unpredicted.err.png,align=left,caption="",selflink)]] 연구자는 데이터를 이용하여 회귀식의 b값과 a값을 구할 수 있다. 그리고 이를 사용하면, 평균값 $\overline{Y}$ 이 주는 오차에 비해서 상대적으로 작은 (녹색선만큼을 뺀 분량의) 오차를 갖도록 할 수 있다. 즉, 회귀식이 보다 정확한 예측을 가능하도록 하여 주는 것이다. 이렇게 회귀식을 사용하여 (즉, b라는 기울기를 사용하여) 관측치를 예측함으로써, 평균값을 사용했을 때보다 줄어드는 오차 부분을 설명된 오차라고 (explained error) 한다. 그러나, 회귀선을 사용하더라도 연구자는 검은색 만큼의 오차는 피할 수 없다. 이를 '''설명되지 않은 오차'''라고 (unexplained error) 한다. 그리고 이 각각을 regression error 와 residual error라고 부른다.
위 그림의 예를 보면, X,,i,,의 값이 15일때,
@@ -148,7 +153,10 @@
따라서 $\text{Total variablity of Y = Explained variablility + Unexplained variability} $ 라고 표현할 수 있다.
$SS_{unexplained} = \sum (Y_i-\hat {Y})^2$ 의 값에 df 값인 (N-2) 을 나누어 준 후 루트를 씌워 준 값을 '''추정치에 대한 표준 오차'''라고 부르며 ( $s_{total}$ 혹은 $s_{Y.X}$ 이라고 기록한다. 이 값에 제곱한 값을 '''잔여 변량''' 혹은 '''오차 변량'''이라고 부른다 ( $(S_{Y.X})^2$ 혹은 $\frac{SS_{res}}{df}$ ). 이에 대한 부연설명은 아래에서 다시 하도록 하겠다.
$SS_{unexplained} = \sum (Y_i-\hat {Y})^2$ 의 값에 df 값인 (N-2) 을 나누어 준 후 루트를 씌워 준 값을 '''추정치에 대한 표준 오차'''라고 부르며
이 값을 제곱한 값을 '''잔여 변량 (residual variance)''' 혹은 '''오차 변량(error variance)'''이라고 부른다
이에 대한 부연설명은 아래에서 다시 하도록 하겠다.
Data file: attachment:regression01-bankAccount.sav
@@ -209,7 +217,7 @@
(Intercept) 3.617781 1.241518 2.914 0.01947 * income 0.015269 0.004127 3.700 0.00605 **
---
Sig. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.176 on 8 degrees of freedom
Multiple R-squared: 0.6311, Adjusted R-squared: 0.585
@@ -261,9 +269,13 @@
위에서, SS에 해당되는 것만 살펴보면 (양쪽의 표준편차의 분모를 제외하고 제곱을 하여 보면),
{{{#!latex
\begin{eqnarray*}
\displaystyle SS_{res} & = & SS_{total} (1-r^2) \\
\displaystyle r^2 & = & \frac{SS_{total} - SS_{res}}{SS_{total}} \\
\displaystyle r^2 & = & \frac{SS_{reg}}{SS_{total}} \\
\end{eqnarray*}
}}}
과 같이 표현할 수 있다. 위의 공식을 말로 바꿔 설명해 보면,
@@ -280,7 +292,7 @@
|| b |||||||||||| Dependent Variable: bankbook number of bank ||[[HTML(<div style='clear:both'> </div>)]]
__SS,,total,, SS,,reg,, SS,,res,, 를 이용한 F-test__
__ SS,,total SS,,reg,, SS,,res,, 를 이용한 F-test__
회귀공식 (regression equation) 혹은 모델 (regression model)이 만들어지게 되면 이 모델에 대한 판단이 필요하다. 첫 째, regression equation에서 도출되는 잔여오차 (SS,,res,, )가 충분히 작은지 (혹은 거꾸로, regression equation에 의해서 설명된 오차 (SS,,reg,, )가 전체오차를 (SS,,total,, ) 줄이는데 충분했는지이다. 이는 r^2^ 에 대한 판단을 통해서 하게 되는데, 이 때 사용되는 것이 F-test이다. 또한, 변인이 갖는 계수 (coefficient) 값 ( $\hat{Y} = a + bX $ 에서 b 값)이 r^2^ 값에 얼마나 기여했는가를 판단하는 것이다. 이 경우에는 b값에 대한 (즉, 기울기에 대한) t-test를 이용하게 된다.
@@ -310,7 +322,8 @@
|| Model || R || R Square || Adjusted R Square || Std. Error of the Estimate || |||| 1.000 || 0.794 || 0.631 || 0.585 || 1.176 || ||
|| a |||||||||| Predictors: (Constant), bankIncome income ||
[[HTML(<div style='clear:both'> </div>)]]
그렇다면, 여기서
@@ -327,7 +340,8 @@
|| 1.000 || (Constant) || 3.618 || 1.242 || || 2.914 || 0.019 |||| || bankIncome income || 0.015 || 0.004 || 0.794 || 3.700 || 0.006 ||
|| a |||||||||||| Dependent Variable: bankbook number of bank||
[[HTML(<div style='clear:both'> </div>)]]
이 때, (t,,b,,)^^2^^ = F value.
== Data examination ==
@@ -645,6 +659,7 @@
|| ||100 ||81 ||20.3 ||20.3 ||100.0 |||| ||Total ||400 ||100.0 ||100.0 || ||
[[HTML(<div style='clear:both'> </div>)]]
frequencies
variables=full .
1. 단순회귀분석 ¶
두 변인 간의 상관관계가 완전하다면 (r=1.0 혹은 r=-1.0) 변인 간의 상관관계에 의한 그래프는 아래와 같을 것이다.
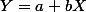
그리고 이렇게 해서 얻는 곡선을 회귀 곡선이라고 (regression line) 하며, 이 곡선을 표현하는 등식을 회귀방정식 (regression equation)이라고 한다. 실제에서는 r 값이 1 혹은 -1인 경우가 드물다. 이것이 의미하는 것은 데이터가 어느 일정한 방향성과 응집성을 가지고는 있으나, 이것이 완변한 선형을 이루지는 않는다는 것을 의미한다 (그림 참조). 이와 같은 데이터에도 회귀곡선을 그릴 수 있는데 (따라서 회귀식을 구할 수 있는데) 이 장에서는 이에 대해서 설명한다.
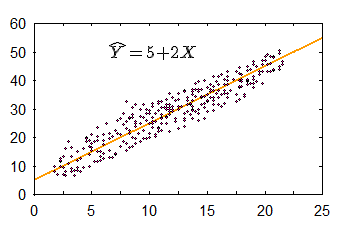
r=- 1이 아닌 회귀선과 데이터 [PNG image (5.92 KB)]
그림에서 보는 것처럼, 실제 데이터에서 얻게 되는 회귀 방정식은 정확한 데이터의 움직임을 나타내 줄 수는 없으므로 추정치를 표시하는 지표로 사용된다.
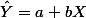
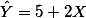
추정치와 관측치 간의 차이=오차 [PNG image (7.96 KB)]
여기서 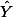 는
는 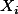 에서 실제 데이터 값을 (
에서 실제 데이터 값을 ( 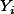 ) 추정해주는 값을 말하며 Y hat이라고 읽는다. 완벽한 correlatin이 아닐 경우에
) 추정해주는 값을 말하며 Y hat이라고 읽는다. 완벽한 correlatin이 아닐 경우에 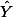 의 값은 실제
의 값은 실제 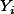 값과 다를 수 있다. 회귀식을 이용하여 구한
값과 다를 수 있다. 회귀식을 이용하여 구한 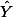 값은 기대치 혹은 예측치라고 할 수 있으며, 데이터를 이용하여 알아낸
값은 기대치 혹은 예측치라고 할 수 있으며, 데이터를 이용하여 알아낸 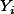 값은 관측치 혹은 실측치라고 할 수 있는데 이와 같이 실제 데이터의 관측치와 기대치와의 차이는 그림에서 괄호로 묶은 부분을 의미하며 이는
값은 관측치 혹은 실측치라고 할 수 있는데 이와 같이 실제 데이터의 관측치와 기대치와의 차이는 그림에서 괄호로 묶은 부분을 의미하며 이는  로 표현한다.
로 표현한다.
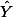 는
는  에서 실제 데이터 값을 (
에서 실제 데이터 값을 ( 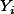 ) 추정해주는 값을 말하며 Y hat이라고 읽는다. 완벽한 correlatin이 아닐 경우에
) 추정해주는 값을 말하며 Y hat이라고 읽는다. 완벽한 correlatin이 아닐 경우에 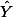 의 값은 실제
의 값은 실제 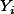 값과 다를 수 있다. 회귀식을 이용하여 구한
값과 다를 수 있다. 회귀식을 이용하여 구한 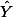 값은 기대치 혹은 예측치라고 할 수 있으며, 데이터를 이용하여 알아낸
값은 기대치 혹은 예측치라고 할 수 있으며, 데이터를 이용하여 알아낸 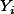 값은 관측치 혹은 실측치라고 할 수 있는데 이와 같이 실제 데이터의 관측치와 기대치와의 차이는 그림에서 괄호로 묶은 부분을 의미하며 이는
값은 관측치 혹은 실측치라고 할 수 있는데 이와 같이 실제 데이터의 관측치와 기대치와의 차이는 그림에서 괄호로 묶은 부분을 의미하며 이는  로 표현한다.
로 표현한다.상관관계에서 살펴 본것처럼, 관측된 데이터는 최소자승 (Least Squared) 법을 이용하여 회귀식을 유도할 수 있는데, 이때의 절편과 기울기 값은 각각 다음과 같이 구할 수 있다:
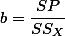
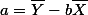
최소자승이 의미하는 것은 위의 그림과 같다. regression line (회귀선)으로 X 값에 해당하는 Y 값을 예측할 수 있는데, 이때에는 실측값과 차이가 날 수 있다. 이 차이가 위의 그림에서 녹색선인데, 이 녹색선의 합이 최소값을 갖도록하는 것을 최소자승(least squared)법이라고 한다.
간혹, 다른 교재를 보면,
와 같이 나타나는데 이 둘은 같은 의미를 갖는다.
동일한 공식 설명:
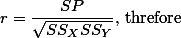
그리고
따라서
따라서
아래 예를 살펴보자.
| 국어와 영어 점수 간의 상관관계 | ||
| Korean | English | |
| A | 1 | 1 |
| B | 4 | 2 |
| C | 5 | 4 |
| D | 3 | 3 |
| E | 7 | 5 |
| 국어와 영어 점수 간의 상관관계 | |||||
| X | Y | 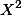 | 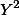 |  | |
| A | 1 | 1 | 1 | 1 | 1 |
| B | 4 | 2 | 16 | 4 | 8 |
| C | 5 | 4 | 25 | 16 | 20 |
| D | 3 | 3 | 9 | 9 | 9 |
| E | 7 | 5 | 49 | 25 | 35 |
 |  |  |  |  | |
 |  | ||||
위에서,
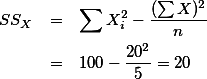
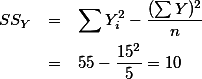
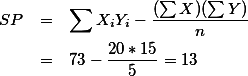
따라서
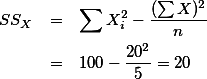
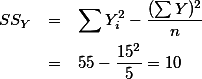
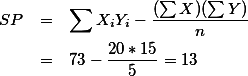
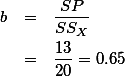
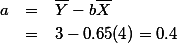
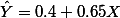
 . 그리고, 이는 회귀곡선을 이용한 예측치가 갖는 오차이다. 이를 residual error라고 표기한다. 각각의 Yi 에 대해서 residual error 를 구할 수 있는데, 이 오차의 제곱의 합을 SSres 라고 표현하게 된다. 이에 대한 자세한 설명은 아래에서 하도록 한다.
. 그리고, 이는 회귀곡선을 이용한 예측치가 갖는 오차이다. 이를 residual error라고 표기한다. 각각의 Yi 에 대해서 residual error 를 구할 수 있는데, 이 오차의 제곱의 합을 SSres 라고 표현하게 된다. 이에 대한 자세한 설명은 아래에서 하도록 한다.2. 표준오차 잔여변량 (standard error, residual) ¶
아래 그림은 변인 X 와 Y 간의 관계를 (association) 나타내주는 그래프이다. 그리고, 이 그래프에서  이다. 이 데이터 중에서 X에 대한 정보가 없다고 가정하고, Y 관측치를 예측하려면 어떻게 해야 할까? 당연히 연구자는 자신이 가지고 있는 Y 변인 데이터의 중앙값인 평균 (
이다. 이 데이터 중에서 X에 대한 정보가 없다고 가정하고, Y 관측치를 예측하려면 어떻게 해야 할까? 당연히 연구자는 자신이 가지고 있는 Y 변인 데이터의 중앙값인 평균 ( 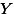 ) 을 사용하려고 할 것이다. 그러나, 연구자가 Y 변인의 평균값을 Y의 대표값이라고 하기에는 개인의 실제값 (혹은 관측치)과 평균값 간의 오차가 너무 크다. 이 오차를 줄이기 위해서 만들어진 것이 회귀선이다 (regression line, 오렌지 라인). 따라서 회귀선은 평균값만을 사용할 때 나타나는 오차를 줄여주는 역할을 한다. 이렇게 줄어든 오차를 설명된 오차라고 (explained error) 한다. 예를 들면, 아래 그림에서
) 을 사용하려고 할 것이다. 그러나, 연구자가 Y 변인의 평균값을 Y의 대표값이라고 하기에는 개인의 실제값 (혹은 관측치)과 평균값 간의 오차가 너무 크다. 이 오차를 줄이기 위해서 만들어진 것이 회귀선이다 (regression line, 오렌지 라인). 따라서 회귀선은 평균값만을 사용할 때 나타나는 오차를 줄여주는 역할을 한다. 이렇게 줄어든 오차를 설명된 오차라고 (explained error) 한다. 예를 들면, 아래 그림에서  일때의 Y 값의 하나인
일때의 Y 값의 하나인 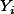 값은 평균값인
값은 평균값인 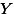 값에서 녹색선과 검은색 선의 길이만큼의 오차를 갖는다. 이렇게 된 이유는 연구자가 오직 Y 값만을 분석하여 Y 값을 예측했기 때문이다.
값에서 녹색선과 검은색 선의 길이만큼의 오차를 갖는다. 이렇게 된 이유는 연구자가 오직 Y 값만을 분석하여 Y 값을 예측했기 때문이다.
 이다. 이 데이터 중에서 X에 대한 정보가 없다고 가정하고, Y 관측치를 예측하려면 어떻게 해야 할까? 당연히 연구자는 자신이 가지고 있는 Y 변인 데이터의 중앙값인 평균 (
이다. 이 데이터 중에서 X에 대한 정보가 없다고 가정하고, Y 관측치를 예측하려면 어떻게 해야 할까? 당연히 연구자는 자신이 가지고 있는 Y 변인 데이터의 중앙값인 평균 ( 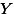 ) 을 사용하려고 할 것이다. 그러나, 연구자가 Y 변인의 평균값을 Y의 대표값이라고 하기에는 개인의 실제값 (혹은 관측치)과 평균값 간의 오차가 너무 크다. 이 오차를 줄이기 위해서 만들어진 것이 회귀선이다 (regression line, 오렌지 라인). 따라서 회귀선은 평균값만을 사용할 때 나타나는 오차를 줄여주는 역할을 한다. 이렇게 줄어든 오차를 설명된 오차라고 (explained error) 한다. 예를 들면, 아래 그림에서
) 을 사용하려고 할 것이다. 그러나, 연구자가 Y 변인의 평균값을 Y의 대표값이라고 하기에는 개인의 실제값 (혹은 관측치)과 평균값 간의 오차가 너무 크다. 이 오차를 줄이기 위해서 만들어진 것이 회귀선이다 (regression line, 오렌지 라인). 따라서 회귀선은 평균값만을 사용할 때 나타나는 오차를 줄여주는 역할을 한다. 이렇게 줄어든 오차를 설명된 오차라고 (explained error) 한다. 예를 들면, 아래 그림에서  일때의 Y 값의 하나인
일때의 Y 값의 하나인 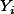 값은 평균값인
값은 평균값인 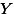 값에서 녹색선과 검은색 선의 길이만큼의 오차를 갖는다. 이렇게 된 이유는 연구자가 오직 Y 값만을 분석하여 Y 값을 예측했기 때문이다.
값에서 녹색선과 검은색 선의 길이만큼의 오차를 갖는다. 이렇게 된 이유는 연구자가 오직 Y 값만을 분석하여 Y 값을 예측했기 때문이다. 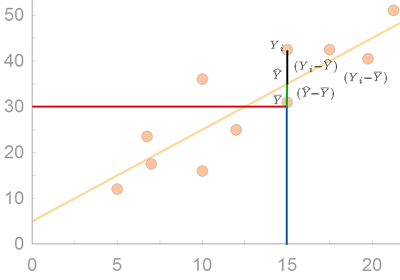
"" [PNG image (17.5 KB)]
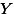 이 주는 오차에 비해서 상대적으로 작은 (녹색선만큼을 뺀 분량의) 오차를 갖도록 할 수 있다. 즉, 회귀식이 보다 정확한 예측을 가능하도록 하여 주는 것이다. 이렇게 회귀식을 사용하여 (즉, b라는 기울기를 사용하여) 관측치를 예측함으로써, 평균값을 사용했을 때보다 줄어드는 오차 부분을 설명된 오차라고 (explained error) 한다. 그러나, 회귀선을 사용하더라도 연구자는 검은색 만큼의 오차는 피할 수 없다. 이를 설명되지 않은 오차라고 (unexplained error) 한다. 그리고 이 각각을 regression error 와 residual error라고 부른다.
이 주는 오차에 비해서 상대적으로 작은 (녹색선만큼을 뺀 분량의) 오차를 갖도록 할 수 있다. 즉, 회귀식이 보다 정확한 예측을 가능하도록 하여 주는 것이다. 이렇게 회귀식을 사용하여 (즉, b라는 기울기를 사용하여) 관측치를 예측함으로써, 평균값을 사용했을 때보다 줄어드는 오차 부분을 설명된 오차라고 (explained error) 한다. 그러나, 회귀선을 사용하더라도 연구자는 검은색 만큼의 오차는 피할 수 없다. 이를 설명되지 않은 오차라고 (unexplained error) 한다. 그리고 이 각각을 regression error 와 residual error라고 부른다.위 그림의 예를 보면, Xi의 값이 15일때,
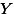 ) 얼마나 떨어져 있을까라는 질문에는 각각의 Yi값이 Y 평균값에서 얼마나 떨어져 있는가 (deviation score)를 계산하여 제곱한 후, 이를 모두 더하면 Y값에 대한 SS 값을 구할 수 있을 것이다. 이를 df로 나누어 주면 전체 Y값에 대한 분산값을 구할 수 있겠다. 이것을 전체에러자승 (SStotal ) 이라고 한다.
) 얼마나 떨어져 있을까라는 질문에는 각각의 Yi값이 Y 평균값에서 얼마나 떨어져 있는가 (deviation score)를 계산하여 제곱한 후, 이를 모두 더하면 Y값에 대한 SS 값을 구할 수 있을 것이다. 이를 df로 나누어 주면 전체 Y값에 대한 분산값을 구할 수 있겠다. 이것을 전체에러자승 (SStotal ) 이라고 한다.
- 실제 데이터인 Y값은, Yi로 표현 할 수 있고 (푸른색 + 녹색 + 검정색),
- 추정치인 Y 값은,
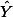 (Y hat 이라고 읽는다) 으로 표현 할 수 있으며 (푸른색+ 녹색),
(Y hat 이라고 읽는다) 으로 표현 할 수 있으며 (푸른색+ 녹색),
- 전체 Y값의 평균은
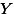 로 표현할 수 있다 (푸른색).
로 표현할 수 있다 (푸른색).
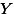 ) 얼마나 떨어져 있을까라는 질문에는 각각의 Yi값이 Y 평균값에서 얼마나 떨어져 있는가 (deviation score)를 계산하여 제곱한 후, 이를 모두 더하면 Y값에 대한 SS 값을 구할 수 있을 것이다. 이를 df로 나누어 주면 전체 Y값에 대한 분산값을 구할 수 있겠다. 이것을 전체에러자승 (SStotal ) 이라고 한다.
) 얼마나 떨어져 있을까라는 질문에는 각각의 Yi값이 Y 평균값에서 얼마나 떨어져 있는가 (deviation score)를 계산하여 제곱한 후, 이를 모두 더하면 Y값에 대한 SS 값을 구할 수 있을 것이다. 이를 df로 나누어 주면 전체 Y값에 대한 분산값을 구할 수 있겠다. 이것을 전체에러자승 (SStotal ) 이라고 한다.특정 케이스를 (즉, (Xi, Yi)의 값) 살펴보면, 이 때의 Yi값이 Y의 평균값에서 떨어져 있는 거리를 편차점수라고 한다면, 이 점수는 아래와 같이 구할 수 있다. 즉, 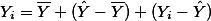 이며, 따라서,
이며, 따라서, 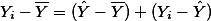 라고 할 수 있다. 혹은 우리가 이전에 다루었던 것을 생각해 보면, 이 점수는 바로 Sum of Square (SS) 점수이다.
라고 할 수 있다. 혹은 우리가 이전에 다루었던 것을 생각해 보면, 이 점수는 바로 Sum of Square (SS) 점수이다.
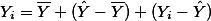 이며, 따라서,
이며, 따라서, 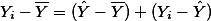 라고 할 수 있다. 혹은 우리가 이전에 다루었던 것을 생각해 보면, 이 점수는 바로 Sum of Square (SS) 점수이다.
라고 할 수 있다. 혹은 우리가 이전에 다루었던 것을 생각해 보면, 이 점수는 바로 Sum of Square (SS) 점수이다. 그런데, 이 그림에서 녹색 부분을 보면, 이를 설명된 편차라고 (explained deviation) 할 수 있다. 왜냐하면, Yi값이 평균에서 떨어져 있는 편차점수 중 이 거리에 해당하는 것은 회귀곡선에 의해서 설명되기 때문이다. 반면에 그림에서 흑색 부분에 해당하는 거리는 설명되지 않은 편차라고 (unexplained deviation) 할 수 있다. 평균에서 떨어진 총 편차 중 이 거리는 회귀곡선이 설명하지 못하기 때문이다. 이와 같이 설명된 편차와 설명되지 않은 편차의 합을 (정확히는 각각의 값을 제곱해서 모두 더한 값) 총 편차라고 ( SStotal ) 한다.
따라서 Y 평균 값에 대한 Yi값의 총 편차 값은 설명된 편차와 설명되지 않은 편차로 이루어져 있다.
모든 케이스에 대한 총편차와 설명된 편차, 설명되지 않은 편차 값을 구해서 각각 더해 보면 그 합은 모두 0이 된다. 따라서, 각각의 총편차 값와 설명편차값, 설명되지 않은 편차 값을 제곱한 후 모두 더해 주면 위에서 소개한 것처럼 전체 Y 분산값을 구하기 위한 SS값이 된다. 이를 Sum of Square of Total deviations 혹은 Total variation이라고 하며, 아래와 같이 나타낼 수 있다.
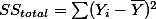
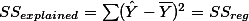
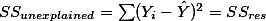
따라서 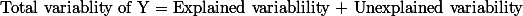 라고 표현할 수 있다.
라고 표현할 수 있다.
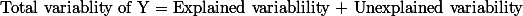 라고 표현할 수 있다.
라고 표현할 수 있다.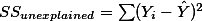 의 값에 df 값인 (N-2) 을 나누어 준 후 루트를 씌워 준 값을 추정치에 대한 표준 오차라고 부르며
의 값에 df 값인 (N-2) 을 나누어 준 후 루트를 씌워 준 값을 추정치에 대한 표준 오차라고 부르며 이 값을 제곱한 값을 잔여 변량 (residual variance) 혹은 오차 변량(error variance)이라고 부른다
이에 대한 부연설명은 아래에서 다시 하도록 하겠다.
3. E.g., 1. Simple regression & F-test for goodness of fit ¶
Data file:  regression01-bankAccount.sav (650 Bytes)
regression01-bankAccount.sav (650 Bytes)
 regression01-bankAccount.sav (650 Bytes)
regression01-bankAccount.sav (650 Bytes)아래는 어느 책에서 쓰인 가상 데이터이다. 통장수와 수입, 그리고 가족 구성원의 숫자가 변인이며 총 10 가구에 대한 정보가 수집된 것이다. 여기서는 이 데이터를 이용하여 위에서 언급된 SStotal , SSreg , SSres 에 대한 예를 살펴보도록 한다.
SStotal , 전체에러
| DATA for regression analysis | ||
| bankaccount | income | famnum |
| 6 | 220 | 5 |
| 5 | 190 | 6 |
| 7 | 260 | 3 |
| 7 | 200 | 4 |
| 8 | 330 | 2 |
| 10 | 490 | 4 |
| 8 | 210 | 3 |
| 11 | 380 | 2 |
| 9 | 320 | 1 |
| 9 | 270 | 3 |
| m = 8 | 287 | 3.3 |
연구자가 이 데이터를 구한 이유는 통장의 숫자에 (account) 영향을 주는 것으로 가구의 수입(income) (과 가족숫자) 이 있을 것이라고 예상했기 때문이다 [1]. 연구자는 이 데이터의 기술적인 통계를 살펴보고, account변인의 평균이 8임을 알게 되었다.
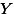 를 사용한 것은 자연스러운 판단이라고 생각된다.
를 사용한 것은 자연스러운 판단이라고 생각된다.
account income fammember
Min. : 5 Min. :190.0 Min. :1.00
1st Qu.: 7 1st Qu.:212.5 1st Qu.:2.25
Median : 8 Median :265.0 Median :3.00
Mean : 8 Mean :287.0 Mean :3.30
3rd Qu.: 9 3rd Qu.:327.5 3rd Qu.:4.00
Max. :11 Max. :490.0 Max. :6.00
아래는 평균값인 8만을 이용해서 Y값을 예측해 본 후에 이 예측값과 측정값 (원래데이터)의 차이를 구한후 (error column) 이를 다시 제곱한 것을 (error2 ) 정리한 표이다. 연구자는 현재 Y에 대한 정보만을 가지고 Y값을 예측하는 상황이다. 따라서, 평균값인 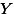 를 사용한 것은 자연스러운 판단이라고 생각된다.
를 사용한 것은 자연스러운 판단이라고 생각된다. prediction for y values with 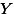 | ||
| bankaccount | error | error^2 |
| 6 | -2 | 4 |
| 5 | -3 | 9 |
| 7 | -1 | 1 |
| 7 | -1 | 1 |
| 8 | 0 | 0 |
| 10 | 2 | 4 |
| 8 | 0 | 0 |
| 11 | 3 | 9 |
| 9 | 1 | 1 |
| 9 | 1 | 1 |
 | 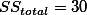 | |
위에서 제곱한 값의 합은? 30이다. 이는 사실, SS (Sum of Square)값이 30이라는 이야기이다. 그리고, 위에서 설명한 것처럼, 이 값은
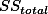 이라고 할 수 있으며 전체에러 변량이라고 할 수 있겠다.
이라고 할 수 있으며 전체에러 변량이라고 할 수 있겠다.SSres , Residual error
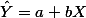
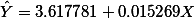
라고 정리할 수 있는데. . . .
아래는 이 공식을 이용하여 구한 Y의 예측값을 구한 후 (pred1), 이 값과 실제값(account)의 차이값을 구한 후 (error1), 이를 다시 제곱한 값을 (error2 ) 정리한 표이다.
Residuals:
Min 1Q Median 3Q Max
-1.5189 -0.8969 -0.1297 1.0058 1.5800
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.617781 1.241518 2.914 0.01947 *
income 0.015269 0.004127 3.700 0.00605 **
---
Sig. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.176 on 8 degrees of freedom
Multiple R-squared: 0.6311, Adjusted R-squared: 0.585
F-statistic: 13.69 on 1 and 8 DF, p-value: 0.006046
위의 계산에서: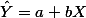
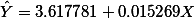
아래는 이 공식을 이용하여 구한 Y의 예측값을 구한 후 (pred1), 이 값과 실제값(account)의 차이값을 구한 후 (error1), 이를 다시 제곱한 값을 (error2 ) 정리한 표이다.
| prediction for y values with regression | |||
| bankaccount | pred1 | error1 | error^2 |
| 6 | 6.977 | 0.977 | 0.954 |
| 5 | 6.519 | 1.519 | 2.307 |
| 7 | 7.588 | 0.588 | 0.345 |
| 7 | 6.672 | -0.328 | 0.108 |
| 8 | 8.657 | 0.657 | 0.431 |
| 10 | 11.100 | 1.100 | 1.209 |
| 8 | 6.824 | -1.176 | 1.382 |
| 11 | 9.420 | -1.580 | 2.496 |
| 9 | 8.504 | -0.496 | 0.246 |
| 9 | 7.740 | -1.260 | 1.587 |
| 8 |  | ||
여기서 구한 SS 값은? 이는 regression 곡선을 이용하여 Y값을 예측하였음에도 불구하고, 극복하지 못한 오차 (제곱의 합) 이다. 즉, 이는 SSres 에 해당하는 값이다. 그리고 이를 이용하여 SSreg 값을 구해보면 아래와 같다.
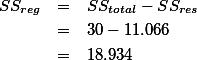
| ANOVA(b) | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1.000 | Regression | 18.934 | 1.000 | 18.934 | 13.687 | 0.006 |
| Residual | 11.066 | 8.000 | 1.383 | |||
| Total | 30.000 | 9.000 | ||||
| a | Predictors: (Constant), bankIncome income | |||||
| b | Dependent Variable: bankbook number of bank | |||||
SStotal SSreg SSres,, 를 이용한 F-test
회귀공식 (regression equation) 혹은 모델 (regression model)이 만들어지게 되면 이 모델에 대한 판단이 필요하다. 첫 째, regression equation에서 도출되는 잔여오차 (SSres )가 충분히 작은지 (혹은 거꾸로, regression equation에 의해서 설명된 오차 (SSreg )가 전체오차를 (SStotal ) 줄이는데 충분했는지이다. 이는 r2 에 대한 판단을 통해서 하게 되는데, 이 때 사용되는 것이 F-test이다. 또한, 변인이 갖는 계수 (coefficient) 값 ( 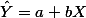 에서 b 값)이 r2 값에 얼마나 기여했는가를 판단하는 것이다. 이 경우에는 b값에 대한 (즉, 기울기에 대한) t-test를 이용하게 된다.
에서 b 값)이 r2 값에 얼마나 기여했는가를 판단하는 것이다. 이 경우에는 b값에 대한 (즉, 기울기에 대한) t-test를 이용하게 된다.
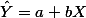 에서 b 값)이 r2 값에 얼마나 기여했는가를 판단하는 것이다. 이 경우에는 b값에 대한 (즉, 기울기에 대한) t-test를 이용하게 된다.
에서 b 값)이 r2 값에 얼마나 기여했는가를 판단하는 것이다. 이 경우에는 b값에 대한 (즉, 기울기에 대한) t-test를 이용하게 된다. 위 섹션에서,
white = explained error (E) = 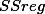
orange = unexplained error (U) =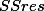
yellow = total error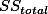 = E + U =
= E + U = 
degrees of freedom 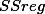
orange = unexplained error (U) =
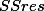
yellow = total error
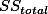 = E + U =
= E + U = 
white red (number of variable -1) = 1 (blue)
for orange (number of case - number of variable) = 8 (green)
Then, for orange (number of case - number of variable) = 8 (green)
what is MS = variance = 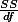 ?
?
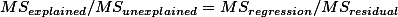 ?
?
- F-value for evaluating r2 portion turns out to be significant.
- F = xxx, which means . . . . X를 이용하여 Y의 변화를 이야기할 수 있는 부분인 R2 값이 통계학적으로 유의미한가를 판단할 수 있도록 도와주었다는 것 (goodness of fit).
From the above table, check out that the value of R2 = 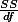 ?
?for regression (explained portion) and ?
for residual residual (unexplained portion) ?
Then, what is for residual residual (unexplained portion) ?
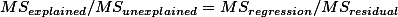 ?
?- F = xxx, which means . . . . X를 이용하여 Y의 변화를 이야기할 수 있는 부분인 R2 값이 통계학적으로 유의미한가를 판단할 수 있도록 도와주었다는 것 (goodness of fit).
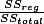 and compare the value to that in the below table.
and compare the value to that in the below table. | Model Summary | |||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate | |
| 1.000 | 0.794 | 0.631 | 0.585 | 1.176 | |
| a | Predictors: (Constant), bankIncome income | ||||
= 63.1% 즉, Y의 변량 중에서 X를 이용하여 설명할 수 있는 부분이 약 63%이고 이 분석을 적용할때, 잘 못될 확률, p = 0.006 .
그렇다면, 여기서 Y = a + bX 에서 b 가 R2 에 얼마나 기여했는가?
-> r2 만큼 했다고 말하는 것이 상식적이다. 왜냐하면, r2 에 기여한 변인으로 오직 하나 있는 것이 X변인이기 때문이다.
| Coefficients(a) | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Std. Error | Beta | ||||
| 1.000 | (Constant) | 3.618 | 1.242 | 2.914 | 0.019 | |
| bankIncome income | 0.015 | 0.004 | 0.794 | 3.700 | 0.006 | |
| a | Dependent Variable: bankbook number of bank | |||||
위에서 tb = 3.700, p = .006
이 때, (tb)2 = F value.
4. Data examination ¶
Here we are looking at several variables, instead of each of IV and DV. This is called multiple regression. We will discuss it later.
| Data Label description | ||
| Variable Labels | ||
| Variable | Position | Label |
| snum | 1 | school number |
| dnum | 2 | district number |
| api00 | 3 | api 2000 |
| api99 | 4 | api 1999 |
| growth | 5 | growth 1999 to 2000 |
| meals | 6 | pct free meals |
| ell | 7 | english language learners |
| yr_rnd | 8 | year round school |
| mobility | 9 | pct 1st year in school |
| acs_k3 | 10 | avg class size k-3 |
| acs_46 | 11 | avg class size 4-6 |
| not_hsg | 12 | parent not hsg |
| hsg | 13 | parent hsg |
| some_col | 14 | parent some college |
| col_grad | 15 | parent college grad |
| grad_sch | 16 | parent grad school |
| avg_ed | 17 | avg parent ed |
| full | 18 | pct full credential |
| emer | 19 | pct emer credential |
| enroll | 20 | number of students |
| mealcat | 21 | Percentage free meals in 3 categories |
우리가 관심이 있는 데이터는
2000년의 수학능력 (api00)
% 무료급식
% 풀타임 교원
k-3까지의 평균 클래스사이즈
이에 대한 부분적 자료 먼저 살펴보기 위해서는% 무료급식
% 풀타임 교원
k-3까지의 평균 클래스사이즈
list /variables api00 acs_k3 meals full /cases from 1 to 10.
api00 acs_k3 meals full 693 16 67 76.00 570 15 92 79.00 546 17 97 68.00 571 20 90 87.00 478 18 89 87.00 858 20 . 100.00 918 19 . 100.00 831 20 . 96.00 860 20 . 100.00 737 21 29 96.00 Number of cases read: 10 Number of cases listed: 10
descriptive /var = all .
| Descriptive Statistics | |||||
| N | Minimum | Maximum | Mean | Std. Deviation | |
| school number | 400 | 58 | 6072 | 2866.81 | 1543.811 |
| district number | 400 | 41 | 796 | 457.74 | 184.823 |
| api 2000 | 400 | 369 | 940 | 647.62 | 142.249 |
| api 1999 | 400 | 333 | 917 | 610.21 | 147.136 |
| growth 1999 to 2000 | 400 | -69 | 134 | 37.41 | 25.247 |
| pct free meals | 315 | 6 | 100 | 71.99 | 24.386 |
| english language learners | 400 | 0 | 91 | 31.45 | 24.839 |
| year round school | 400 | 0 | 1 | .23 | .421 |
| pct 1st year in school | 399 | 2 | 47 | 18.25 | 7.485 |
| avg class size k-3 | 398 | -21 | 25 | 18.55 | 5.005 |
| avg class size 4-6 | 397 | 20 | 50 | 29.69 | 3.841 |
| parent not hsg | 400 | 0 | 100 | 21.25 | 20.676 |
| parent hsg | 400 | 0 | 100 | 26.02 | 16.333 |
| parent some college | 400 | 0 | 67 | 19.71 | 11.337 |
| parent college grad | 400 | 0 | 100 | 19.70 | 16.471 |
| parent grad school | 400 | 0 | 67 | 8.64 | 12.131 |
| avg parent ed | 381 | 1.00 | 4.62 | 2.6685 | .76379 |
| pct full credential | 400 | .42 | 100.00 | 66.0568 | 40.29793 |
| pct emer credential | 400 | 0 | 59 | 12.66 | 11.746 |
| number of students | 400 | 130 | 1570 | 483.47 | 226.448 |
| Percentage free meals in 3 categories | 400 | 1 | 3 | 2.02 | .819 |
examine /variables=acs_k3 /plot histogram stem boxplot .
| Descriptives | ||||
| Statistic | Std. Error | |||
| avg class size k-3 | Mean | 18.55 | .251 | |
| 95% Confidence Interval for Mean | Lower Bound | 18.05 | ||
| Upper Bound | 19.04 | |||
| 5% Trimmed Mean | 19.13 | |||
| Median | 19.00 | |||
| Variance | 25.049 | |||
| Std. Deviation | 5.005 | |||
| Minimum | -21 | |||
| Maximum | 25 | |||
| Range | 46 | |||
| Interquartile Range | 2 | |||
| Skewness | -7.106 | .122 | ||
| Kurtosis | 53.014 | .244 | ||
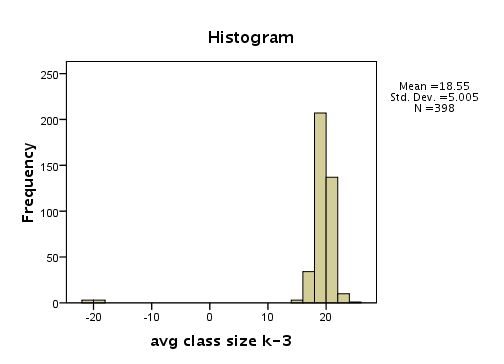
Histogram [JPG image (11.66 KB)]
avg class size k-3 Stem-and-Leaf Plot
Frequency Stem & Leaf
8.00 Extremes (=<14.0)
1.00 15 . &
.00 15 .
14.00 16 . 0000000
.00 16 .
20.00 17 . 0000000000
.00 17 .
64.00 18 . 00000000000000000000000000000000
.00 18 .
143.00 19 . 00000000000000000000000000000000000000000000000000000000000000000000000
.00 19 .
97.00 20 . 000000000000000000000000000000000000000000000000
.00 20 .
40.00 21 . 00000000000000000000
.00 21 .
7.00 22 . 000
.00 22 .
3.00 23 . 0
1.00 Extremes (>=25.0)
Stem width: 1
Each leaf: 2 case(s)
& denotes fractional leaves.
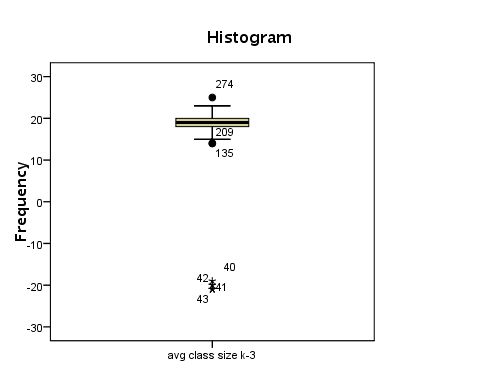
Boxplot [JPG image (9.29 KB)]
frequencies /var acs_k3.
| avg class size k-3 | |||||
| Frequency | Percent | Valid Percent | Cumulative Percent | ||
| Valid | -21 | 3 | .8 | .8 | .8 |
| -20 | 2 | .5 | .5 | 1.3 | |
| -19 | 1 | .3 | .3 | 1.5 | |
| 14 | 2 | .5 | .5 | 2.0 | |
| 15 | 1 | .3 | .3 | 2.3 | |
| 16 | 14 | 3.5 | 3.5 | 5.8 | |
| 17 | 20 | 5.0 | 5.0 | 10.8 | |
| 18 | 64 | 16.0 | 16.1 | 26.9 | |
| 19 | 143 | 35.8 | 35.9 | 62.8 | |
| 20 | 97 | 24.3 | 24.4 | 87.2 | |
| 21 | 40 | 10.0 | 10.1 | 97.2 | |
| 22 | 7 | 1.8 | 1.8 | 99.0 | |
| 23 | 3 | .8 | .8 | 99.7 | |
| 25 | 1 | .3 | .3 | 100.0 | |
| Total | 398 | 99.5 | 100.0 | ||
| Missing | System | 2 | .5 | ||
| Total | 400 | 100.0 | |||
compute filtvar = (acs_k3 < 0). filter by filtvar. list cases /var snum dnum acs_k3.
snum dnum acs_k3
600 140 -20
596 140 -19
611 140 -20
595 140 -21
592 140 -21
602 140 -21
Number of cases read: 6 Number of cases listed: 6
filter off. IF (acs_k3<0) racs_k3=ABS(acs_k3). IF (acs_k3>=0) racs_k3=acs_k3. EXECUTE.
frequencies variables=full /format=notable /histogram .
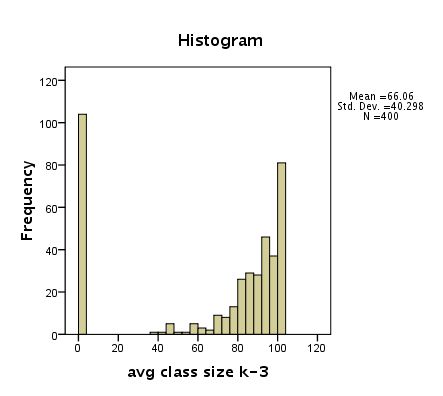
Histogram for variable full [JPG image (12.34 KB)]
| pct full credential | |||||
| Frequency | Percent | Valid Percent | Cumulative Percent | ||
| Valid | 0.42 | 1 | .3 | .3 | .3 |
| 0.45 | 1 | .3 | .3 | .5 | |
| 0.46 | 1 | .3 | .3 | .8 | |
| 0.47 | 1 | .3 | .3 | 1.0 | |
| 0.48 | 1 | .3 | .3 | 1.3 | |
| 0.5 | 3 | .8 | .8 | 2.0 | |
| 0.51 | 1 | .3 | .3 | 2.3 | |
| 0.52 | 1 | .3 | .3 | 2.5 | |
| 0.53 | 1 | .3 | .3 | 2.8 | |
| 0.54 | 1 | .3 | .3 | 3.0 | |
| 0.56 | 2 | .5 | .5 | 3.5 | |
| 0.57 | 2 | .5 | .5 | 4.0 | |
| 0.58 | 1 | .3 | .3 | 4.3 | |
| 0.59 | 3 | .8 | .8 | 5.0 | |
| 0.6 | 1 | .3 | .3 | 5.3 | |
| 0.61 | 4 | 1.0 | 1.0 | 6.3 | |
| 0.62 | 2 | .5 | .5 | 6.8 | |
| 0.63 | 1 | .3 | .3 | 7.0 | |
| 0.64 | 3 | .8 | .8 | 7.8 | |
| 0.65 | 3 | .8 | .8 | 8.5 | |
| 0.66 | 2 | .5 | .5 | 9.0 | |
| 0.67 | 6 | 1.5 | 1.5 | 10.5 | |
| 0.68 | 2 | .5 | .5 | 11.0 | |
| 0.69 | 3 | .8 | .8 | 11.8 | |
| 0.7 | 1 | .3 | .3 | 12.0 | |
| 0.71 | 1 | .3 | .3 | 12.3 | |
| 0.72 | 2 | .5 | .5 | 12.8 | |
| 0.73 | 6 | 1.5 | 1.5 | 14.3 | |
| 0.75 | 4 | 1.0 | 1.0 | 15.3 | |
| 0.76 | 2 | .5 | .5 | 15.8 | |
| 0.77 | 2 | .5 | .5 | 16.3 | |
| 0.79 | 3 | .8 | .8 | 17.0 | |
| 0.8 | 5 | 1.3 | 1.3 | 18.3 | |
| 0.81 | 8 | 2.0 | 2.0 | 20.3 | |
| 0.82 | 2 | .5 | .5 | 20.8 | |
| 0.83 | 2 | .5 | .5 | 21.3 | |
| 0.84 | 2 | .5 | .5 | 21.8 | |
| 0.85 | 3 | .8 | .8 | 22.5 | |
| 0.86 | 2 | .5 | .5 | 23.0 | |
| 0.9 | 3 | .8 | .8 | 23.8 | |
| 0.92 | 1 | .3 | .3 | 24.0 | |
| 0.93 | 1 | .3 | .3 | 24.3 | |
| 0.94 | 2 | .5 | .5 | 24.8 | |
| 0.95 | 2 | .5 | .5 | 25.3 | |
| 0.96 | 1 | .3 | .3 | 25.5 | |
| 1 | 2 | .5 | .5 | 26.0 | |
| 37 | 1 | .3 | .3 | 26.3 | |
| 41 | 1 | .3 | .3 | 26.5 | |
| 44 | 2 | .5 | .5 | 27.0 | |
| 45 | 2 | .5 | .5 | 27.5 | |
| 46 | 1 | .3 | .3 | 27.8 | |
| 48 | 1 | .3 | .3 | 28.0 | |
| 53 | 1 | .3 | .3 | 28.3 | |
| 57 | 1 | .3 | .3 | 28.5 | |
| 58 | 3 | .8 | .8 | 29.3 | |
| 59 | 1 | .3 | .3 | 29.5 | |
| 61 | 1 | .3 | .3 | 29.8 | |
| 63 | 2 | .5 | .5 | 30.3 | |
| 64 | 1 | .3 | .3 | 30.5 | |
| 65 | 1 | .3 | .3 | 30.8 | |
| 68 | 2 | .5 | .5 | 31.3 | |
| 69 | 3 | .8 | .8 | 32.0 | |
| 70 | 1 | .3 | .3 | 32.3 | |
| 71 | 3 | .8 | .8 | 33.0 | |
| 72 | 1 | .3 | .3 | 33.3 | |
| 73 | 2 | .5 | .5 | 33.8 | |
| 74 | 1 | .3 | .3 | 34.0 | |
| 75 | 4 | 1.0 | 1.0 | 35.0 | |
| 76 | 4 | 1.0 | 1.0 | 36.0 | |
| 77 | 2 | .5 | .5 | 36.5 | |
| 78 | 4 | 1.0 | 1.0 | 37.5 | |
| 79 | 3 | .8 | .8 | 38.3 | |
| 80 | 10 | 2.5 | 2.5 | 40.8 | |
| 81 | 4 | 1.0 | 1.0 | 41.8 | |
| 82 | 3 | .8 | .8 | 42.5 | |
| 83 | 9 | 2.3 | 2.3 | 44.8 | |
| 84 | 4 | 1.0 | 1.0 | 45.8 | |
| 85 | 8 | 2.0 | 2.0 | 47.8 | |
| 86 | 5 | 1.3 | 1.3 | 49.0 | |
| 87 | 12 | 3.0 | 3.0 | 52.0 | |
| 88 | 6 | 1.5 | 1.5 | 53.5 | |
| 89 | 5 | 1.3 | 1.3 | 54.8 | |
| 90 | 9 | 2.3 | 2.3 | 57.0 | |
| 91 | 8 | 2.0 | 2.0 | 59.0 | |
| 92 | 7 | 1.8 | 1.8 | 60.8 | |
| 93 | 12 | 3.0 | 3.0 | 63.8 | |
| 94 | 10 | 2.5 | 2.5 | 66.3 | |
| 95 | 17 | 4.3 | 4.3 | 70.5 | |
| 96 | 17 | 4.3 | 4.3 | 74.8 | |
| 97 | 11 | 2.8 | 2.8 | 77.5 | |
| 98 | 9 | 2.3 | 2.3 | 79.8 | |
| 100 | 81 | 20.3 | 20.3 | 100.0 | |
| Total | 400 | 100.0 | 100.0 | ||
frequencies variables=full .
IF (full <= 1) rfull=full * 100. IF (full > 1) rfull=full. EXECUTE.
5. E.g., 2. Simple regression ¶
data:
stream spec83 ph83 Moss 6 6.30 Orcutt 9 6.30 Ellinwood 6 6.30 Jacks 3 6.20 Riceville 5 6.20 Lyons 3 6.10 Osgood 5 5.80 Whetstone 4 5.70 Upper Keyup 1 5.70 West 7 5.70 Boyce 4 5.60 Mormon Hollow 4 5.50 Lawrence 5 5.40 Wilder 0 4.70 Templeton 0 4.50
display labels . output: Variable Labels Variable Position Label stream 1 trubutary of Miller River MA spec83 2 Number of Fish Species ph83 3 Average Summer pH Variables in the working file
Get used with the variable names and labels. Then, grasp a picture what is in the data by examining a few cases.
list /cases from 1 to 5 . output: stream spec83 ph83 Moss 6 6.30 Orcutt 9 6.30 Ellinwood 6 6.30 Jacks 3 6.20 Riceville 5 6.20 Number of cases read: 5 Number of cases listed: 5
list /variables stream spec83 ph83 . output: stream spec83 ph83 Moss 6 6.30 Orcutt 9 6.30 Ellinwood 6 6.30 Jacks 3 6.20 Riceville 5 6.20 Lyons 3 6.10 Osgood 5 5.80 Whetstone 4 5.70 Upper Keyup 1 5.70 West 7 5.70 Boyce 4 5.60 Mormon Hollow 4 5.50 Lawrence 5 5.40 Wilder 0 4.70 Templeton 0 4.50 Number of cases read: 15 Number of cases listed: 15
Take a look at descriptive statistics. They are needed all time for your paper. Note that Warning sign appear since the variable is nominal, which means no descriptive statistics are available.
descriptive /var = all . output: Warnings No statistics are computed for the following variables because they are strings: trubutary of Miller River MA. Descriptive Statistics N Minimum Maximum Mean Std. Deviation Number of Fish Species 15 0 9 4.13 2.503 Average Summer pH 15 4.50 6.30 5.7333 .55506 Valid N (listwise) 15
Explore commands gives more detail information about variables.
Use plots such as histogram, stemleaf, boxplot. Histogram, boxplot are omitted in the below output.
Use plots such as histogram, stemleaf, boxplot. Histogram, boxplot are omitted in the below output.
examine /variables spec83
/plot histogram STEMLEAF boxplot.
output:
Case Processing Summary
Cases
Valid Missing Total
N Percent N Percent N Percent
Number of Fish Species 15 100.0% 0 .0% 15 100.0%
Descriptives
Statistic Std. Error
Number of Fish Species Mean 4.13 .646
95% Confidence Interval for Mean Lower Bound 2.75
Upper Bound 5.52
5% Trimmed Mean 4.09
Median 4.00
Variance 6.267
Std. Deviation 2.503
Minimum 0
Maximum 9
Range 9
Interquartile Range 3
Skewness -.111 .580
Kurtosis -.025 1.121
Number of Fish Species Stem-and-Leaf Plot
Frequency Stem & Leaf
3.00 0 . 001
2.00 0 . 33
6.00 0 . 444555
3.00 0 . 667
1.00 0 . 9
Stem width: *
Each leaf: 1 case(s)
We can also use frequencies command with histogram option in order to get a histogram for ph83.
FREQUENCIES variables = ph83 /format=NOTABLE /histogram . output: Statistics Average Summer pH N Valid 15 Missing 0 + histogram (omitted)
We can also examine the variables with scatterplot with two related variables (IV and DV).
GRAPH /SCATTERPLOT (matrix) = spec83 ph83. output: omitted.
Finally, if the data set does not seem abnormal, we do regression test on two variables. We get three outputs by default.
Variables that are used (Variables Entered/Removed + dependent variable)
Model Summary
ANOVA
Coefficients
Before doing this, what is the IV and DV? What is your theoretical speculation?Model Summary
ANOVA
Coefficients
We assume the quality of water (ph level) would affects (influences) the species of fishes. Hence,
IV:
DV:
DV:
REGRESSION /dependent=spec83 /method=enter ph83. output: Variables Entered/Removed(b) Model Variables Entered Variables Removed Method 1 Average Summer pHa . Enter a. All requested variables entered. b. Dependent Variable: Number of Fish Species Model Summary Model R R Square Adjusted R Square Std. Error of the Estimate 1 .696a .484 .444 1.866 a. Predictors: (Constant), Average Summer pH ANOVA(b) Model Sum of Squares df Mean Square F Sig. 1 Regression 42.462 1 42.462 12.193 .004a Residual 45.272 13 3.482 Total 87.733 14 a. Predictors: (Constant), Average Summer pH b. Dependent Variable: Number of Fish Species Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) -13.855 5.174 -2.678 .019 Average Summer pH 3.138 .899 .696 3.492 .004 a. Dependent Variable: Number of Fish Species
From the above:
What is ANOVA for? :
-- maybe picture needed --model evaluation
What is b for? : The contribution of x's b. In this case (simple regression), since there is only one IV, the only b gets all the credit for the R2 .
What is R and R2 for? R is r (correlation). R is the ratio between SP and SSx SSy . If you put this in English (spoken language), it is the amount of Y's variance that are accounted for with X variance. Or we might say it is the ratio between covariance and product of each variance ( 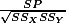 ) . R2 is the actual amount of covariance that is accounted for with the variance of X.
) . R2 is the actual amount of covariance that is accounted for with the variance of X.
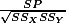 ) . R2 is the actual amount of covariance that is accounted for with the variance of X.
) . R2 is the actual amount of covariance that is accounted for with the variance of X. This is the portion of y's variance that can be explained with the variance of X. In this regression case, it is .484, which we may say, "about 48% of y's variance is accounted for by the variance of X."
And this co-varying is statistically significant, since F (1, 13) = 12.193, p < .01. Also, we can describe the situation with a math formula (an equation).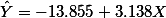
As we can read, as ph-level goes up, the number of specifies of fishes increase. But, ph-level should be positive enough (about 5-6) in order to fish survives (at least one species could be found).
A common sense argues that there is a limit.
SSreg = 42.462
SSres = 45.272
SStotal = 87.733
r2 = SSreg / SStotal = 42.462 / 87.733 = .484.
SSres = 45.272
SStotal = 87.733
r2 = SSreg / SStotal = 42.462 / 87.733 = .484.
6. E.g., 3. Simple regression ¶
This is another example of regression. Here the concept of adjusted r square is explained.
| DATA | |
| x | y |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 2 |
| 5 | 4 |
| Model Summary(b) | ||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | 0.903696114 | 0.816666667 | 0.755555556 | 0.605530071 |
- r-square:
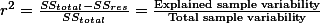
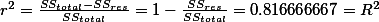
- Usually interpret with % ( by multiplying 100 to
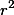 )
)
- Adjusted r-square:
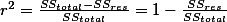 ,
,
- This is equivalent to:
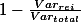
- Var = MS = s2 = SS / n
- Here, we replace the value n
- for Varres = SSres / n - p -1
- for Vartotal = SStotal / n - 1
- for Varres = SSres / n - p -1
- This is the same logic as we used n-1 instead of n in order to get estimation of population standard deviation with a sample statistics.
- Therefore, the Adjusted r2 = 0.755555556
| ANOVA | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 4.9 | 1 | 4.9 | 13.36363636 | 0.035352847 |
| Residual | 1.1 | 3 | 0.366666667 | |||
| Total | 6 | 4 | ||||
| a | Predictors: (Constant), x | |||||
| b | Dependent Variable: y | |||||
- ANOVA, F-test,

- MS_between?
- MS_within?
- MS for residual
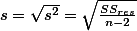
- random difference (MSwithin ):
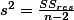
- MS for regression . . . Obtained difference
- do the same procedure at the above in MS for residual.
- but, this time degress of freedom is k-1 (number of variables -1 ), 1.
- do the same procedure at the above in MS for residual.
- Then what does F value mean?
| example | ||||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | 95% Confidence Interval for B | |||
| B | Std. Error | Beta | Lower Bound | Upper Bound | ||||
| 1 | (Constant) | -0.1 | 0.635085296 | -0.157459164 | 0.88488398 | -2.121124854 | 1.921124854 | |
| x | 0.7 | 0.191485422 | 0.903696114 | 3.655630775 | 0.035352847 | 0.090607928 | 1.309392072 | |
| a | Dependent Variable: y | |||||||
- Why do we do t-test for the slope of X variable? The below is a mathematical explanation for this.
- Sampling distribution of Beta:
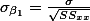
- estimation of
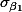 : substitute sigma with s
: substitute sigma with s
- t-test
7. E.g., 4. Simple regression ¶
Another example of simple regression: from  elemapi.sav (31.33 KB) This is the same data set in Data examination. We are interested in the relationship between api00 and enroll
elemapi.sav (31.33 KB) This is the same data set in Data examination. We are interested in the relationship between api00 and enroll
 elemapi.sav (31.33 KB) This is the same data set in Data examination. We are interested in the relationship between api00 and enroll
elemapi.sav (31.33 KB) This is the same data set in Data examination. We are interested in the relationship between api00 and enrolldisplay labels .
| Data Label description | ||
| Variable Labels | ||
| Variable | Position | Label |
| snum | 1 | school number |
| dnum | 2 | district number |
| api00 | 3 | api 2000 |
| api99 | 4 | api 1999 |
| growth | 5 | growth 1999 to 2000 |
| meals | 6 | pct free meals |
| ell | 7 | english language learners |
| yr_rnd | 8 | year round school |
| mobility | 9 | pct 1st year in school |
| acs_k3 | 10 | avg class size k-3 |
| acs_46 | 11 | avg class size 4-6 |
| not_hsg | 12 | parent not hsg |
| hsg | 13 | parent hsg |
| some_col | 14 | parent some college |
| col_grad | 15 | parent college grad |
| grad_sch | 16 | parent grad school |
| avg_ed | 17 | avg parent ed |
| full | 18 | pct full credential |
| emer | 19 | pct emer credential |
| enroll | 20 | number of students |
| mealcat | 21 | Percentage free meals in 3 categories |
enroll: enrollment of students in a school district
api00: academic performance index in 2000
Q: what is the hypothesis here?api00: academic performance index in 2000
regression /dependent api00 /method=enter enroll.
| Model Summaryb | |||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate | |
| 1 | .318a | .101 | .099 | 135.026 | |
| a. Predictors: (Constant), number of students | |||||
| b. Dependent Variable: api 2000 | |||||
| ANOVAb | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 817326.293 | 1 | 817326.293 | 44.829 | .000a |
| Residual | 7256345.704 | 398 | 18232.024 | |||
| Total | 8073671.998 | 399 | ||||
| a. Predictors: (Constant), number of students | ||||||
| b. Dependent Variable: api 2000 | ||||||
| Coefficientsa | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Std. Error | Beta | ||||
| 1 | (Constant) | 744.251 | 15.933 | 46.711 | .000 | |
| number of students | -.200 | .030 | -.318 | -6.695 | .000 | |
| a. Dependent Variable: api 2000 | ||||||
| Residuals Statisticsa | ||||||
| Minimum | Maximum | Mean | Std. Deviation | N | ||
| Predicted Value | 430.46 | 718.27 | 647.62 | 45.260 | 400 | |
| Std. Predicted Value | -4.798 | 1.561 | .000 | 1.000 | 400 | |
| Standard Error of Predicted Value | 6.751 | 33.130 | 8.995 | 3.205 | 400 | |
| Adjusted Predicted Value | 419.51 | 718.81 | 647.64 | 45.452 | 400 | |
| Residual | -285.500 | 389.148 | .000 | 134.857 | 400 | |
| Std. Residual | -2.114 | 2.882 | .000 | .999 | 400 | |
| Stud. Residual | -2.118 | 2.964 | .000 | 1.001 | 400 | |
| Deleted Residual | -286.415 | 411.494 | -.014 | 135.570 | 400 | |
| Stud. Deleted Residual | -2.127 | 2.993 | .000 | 1.003 | 400 | |
| Mahal. Distance | .000 | 23.022 | .997 | 2.245 | 400 | |
| Cook's Distance | .000 | .252 | .003 | .013 | 400 | |
| Centered Leverage Value | .000 | .058 | .003 | .006 | 400 | |
| a. Dependent Variable: api 2000 | ||||||
graph /scatterplot(bivar)=enroll with api00 /missing=listwise .
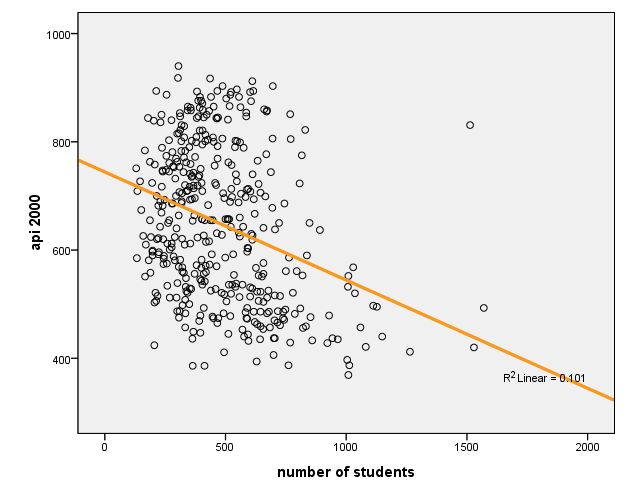
Regression graph eroll by api00 [JPG image (35.01 KB)]
We want to scatterplot for prediction values and standardized residual values.
regression /dependent api00 /method=enter enroll /scatterplot=(*zresid ,*adjpred ) .
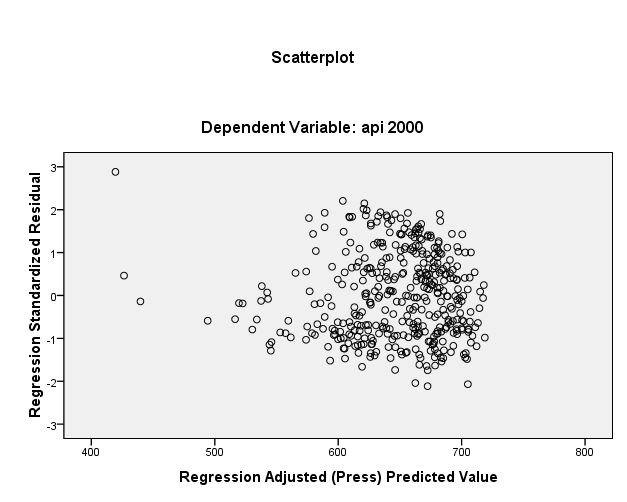
z-residual * adjusted prediction graph [JPG image (32.38 KB)]
For the reference, the below is the terms used in SPSS.
| regression plot | |
| Keyword | Statistic |
| dependnt | dependent variable |
| *zpred | standardized predicted values |
| *zresid | standardized residuals |
| *dresid | deleted residuals |
| *adjpred . | adjusted predicted values |
| *sresid | studentized residuals |
| *sdresid | studentized deleted residuals |
8. regression, for what? ¶
- The prediction power or effects of IVs explained by regression
H1. 과학자들의 성취도는 졸업학교의명성, 직장만족도, 논문숫자, 논문 질에 의해서 설명(예측)될 수 있다.
H1. 방사선연구에 대한 태도는 일반과학에 대한 태도와 원자력연구에 대한 태도에 의해서 설명될 수 있다.
H1. IPTV 프로그램에 대한 호감도는 remote controller 조작의 익숙성, 연령, 가족구성숫자, 경제력에 의해서 예측된다.
H1. 무엇이 보통사람들이 과학관을 찾도록 하는가?
- Each IV's effect could be discerned.
H1. 과학자들의 성취도를 설명하는 졸업학교의명성, 직장만족도, 근무연수, 논문숫자, 그리고 논문질의 설명력에는 차이가 있을 것이다.
H1. 방사선연구에 대한 태도는 일반과학보다는 원자력연구에 대한 태도의 영향을 더 받을 것이다.
- Sometimes, you control some IVs in order to see the pure effect of other IVs
- Model improvement with new IVs
- See interaction effects (will be explained later)
9. Assumptions ¶
- Linearity - the relationships between the predictors and the outcome variable should be linear
- Normality - the errors should be normally distributed - technically normality is necessary only for the t-tests to be valid, estimation of the coefficients only requires that the errors be identically and independently distributed
- Homogeneity of variance (or Homoscedasticity) - the error variance should be constant
- Independence - the errors associated with one observation are not correlated with the errors of any other observation
- Model specification - the model should be properly specified (including all relevant variables, and excluding irrelevant variables)
- Influence - individual observations that exert undue influence on the coefficients
- Collinearity or Singularity - predictors that are highly collinear, i.e. linearly related, can cause problems in estimating the regression coefficients.
10. Assignment ¶
| 예상학점과 클래스 평가 | ||||
| predGP | clsQuality | predGP2 | clsQuality2 | XY |
| 3.50 | 3.40 | 12.25 | 11.56 | 11.9 |
| 3.20 | 2.90 | 10.24 | 8.41 | 9.28 |
| 2.80 | 2.60 | 7.84 | 6.76 | 7.28 |
| 3.30 | 3.80 | 10.89 | 14.44 | 12.54 |
| 3.20 | 3.00 | 10.24 | 9.00 | 9.6 |
| 3.20 | 2.50 | 10.24 | 6.25 | 8 |
| 3.60 | 3.90 | 12.96 | 15.21 | 14.04 |
| 4.00 | 4.30 | 16.00 | 18.49 | 17.2 |
| 3.00 | 3.80 | 9.00 | 14.44 | 11.4 |
| 3.10 | 3.40 | 9.61 | 11.56 | 10.54 |
| 3.00 | 2.80 | 9.00 | 7.84 | 8.4 |
| 3.30 | 2.90 | 10.89 | 8.41 | 9.57 |
| 3.20 | 4.10 | 10.24 | 16.81 | 13.12 |
| 3.40 | 2.70 | 11.56 | 7.29 | 9.18 |
| 3.70 | 3.90 | 13.69 | 15.21 | 14.43 |
| 3.80 | 4.10 | 14.44 | 16.81 | 15.58 |
| 3.80 | 4.20 | 14.44 | 17.64 | 15.96 |
| 3.70 | 3.10 | 13.69 | 9.61 | 11.47 |
| 4.20 | 4.10 | 17.64 | 16.81 | 17.22 |
| 3.80 | 3.60 | 14.44 | 12.96 | 13.68 |
| 3.30 | 4.30 | 10.89 | 18.49 | 14.19 |
| 3.20 | 4.00 | 10.24 | 16.00 | 12.8 |
| 3.10 | 2.10 | 9.61 | 4.41 | 6.51 |
| 3.90 | 3.80 | 15.21 | 14.44 | 14.82 |
| 4.30 | 2.70 | 18.49 | 7.29 | 11.61 |
| 2.90 | 4.40 | 8.41 | 19.36 | 12.76 |
| 3.20 | 3.10 | 10.24 | 9.61 | 9.92 |
| 3.50 | 3.60 | 12.25 | 12.96 | 12.6 |
| 3.30 | 3.90 | 10.89 | 15.21 | 12.87 |
| 3.20 | 2.90 | 10.24 | 8.41 | 9.28 |
| 4.10 | 3.70 | 16.81 | 13.69 | 15.17 |
| 3.50 | 2.80 | 12.25 | 7.84 | 9.8 |
| 3.60 | 3.30 | 12.96 | 10.89 | 11.88 |
| 3.70 | 3.70 | 13.69 | 13.69 | 13.69 |
| 3.30 | 4.20 | 10.89 | 17.64 | 13.86 |
| 3.60 | 2.90 | 12.96 | 8.41 | 10.44 |
| 3.50 | 3.90 | 12.25 | 15.21 | 13.65 |
| 3.40 | 3.50 | 11.56 | 12.25 | 11.9 |
| 3.00 | 3.80 | 9.00 | 14.44 | 11.4 |
| 3.40 | 4.00 | 11.56 | 16.00 | 13.6 |
| 3.70 | 3.10 | 13.69 | 9.61 | 11.47 |
| 3.80 | 4.20 | 14.44 | 17.64 | 15.96 |
| 3.70 | 3.00 | 13.69 | 9.00 | 11.1 |
| 3.70 | 4.80 | 13.69 | 23.04 | 17.76 |
| 3.30 | 3.00 | 10.89 | 9.00 | 9.9 |
| 4.00 | 4.40 | 16.00 | 19.36 | 17.6 |
| 3.60 | 4.40 | 12.96 | 19.36 | 15.84 |
| 3.30 | 3.40 | 10.89 | 11.56 | 11.22 |
| 4.10 | 4.00 | 16.81 | 16.00 | 16.4 |
| 3.30 | 3.50 | 10.89 | 12.25 | 11.55 |
| sum(X) = 174.30 | sum(Y) = 177.50 | |||
| Sx = 0.351 | Sy = 0.614 | |||
| SSx = 613.650 | SSy = 648.570 | SP = 621.94 | ||
----
- [1] 그렇다면 여기서 종속변인과 종속변인은 각각 ( )와 ( )이다