CognitiveDissonanceTheory › Me2DayProjectHkim › CategoryApplyingCommunicationTheoryForProfessionalLife › MDS › IndependentProductions › ConfidenceInterval
About confidence interval.
First, re-read the text book (p.277-288) for brief explanation about standard deviation and my article as well. You should understand the following:
- The standard deviation is a kind of measurement (or indicator) showing the shape of the distribution of a group. If a standard deviation unit is large, it indicates that the shape of the distribution ... plat (platokurtic). If it is small, the shape of the distribution is peak (leptokurtic). In other words, if the a standard unit is large, the individual scores in the particular group do not gather around the mean of the group. And if it is small, they gather around the mean. This is explained in my article.
- The standard deviation can be used to figure out how the areas of a normal curve should be interpreted. That is, if the curve is normal, we can figure out what protion of the population can be found in the distribution in relation to the standard deviation. Words here may confuse you. The 68-95-99 principles is what I am talking about. Again, this is explained in my article or in the text book (p.284-285).
- First, what you are dealing with is not about one sample itself. Rather, we are talking about a kind of distribution of means of (many) samples or distribution of sample means. The individual score in this ditribution curve is a mean of a sample (again, not individual). Having such a distribution curve (of sample means) means that we numerously took samples from a population and kept the record of them. If we do this, the distribution of the scores (again, each score means the mean of a sample) will have a normal distribution curve.
- Having such a normal curve, we can obtain the mean of the distribution curve -- this is the mean of the numerous sample means. Also, we can calculate the standard deviation and assume that the distribution of the scores follows the standard deviation principle -- 68-95-99% rule. And, since each score represents the mean of a sample, we can figure out how the means of samples are distributed. This particular standard deviation is called standard error.
- Based on this standard error, we can argue that if we take many samples from the population, about 68% of the sample means will be found in a specific region -- the mean of the sample means +- one standard error. Or 95% of the sample means will be found in another specific region -- the mean of the sample means +- two standard error. Or 99% of the sample means will be found in another specific region -- the mean of the sample means +- three standard error.
- Of course, in practice, this kind of sampling is not feasible -- that is, having numerous samples. If this is to be done, we would rather get the whole individual scores of the population instead (We call this enumeration). Right? But, what if we can calculate the standard error from just one sample and what if we can use the mean of the sample as the mean of the sample means (like the above)?
- This leads us to the ingeneous way of predicting the mean of the population. For example, we took a sample (IQ score) of 100 people randomly (random sampling is important here) and figured out the mean of the sample and standard error unit. Let's say, the mean score was 100 and standard error was 2.5. From these numbers (mean=100, standard error = 2.5), we can figure out how the sample mans are distributed if we take numerous samples out of the population. That is, about 68% of the sample means will be found in the region of the mean (100) +- One standard error (2.5) -- this is 97.5 - 102.5. Or about 95% of the sample means will be found in the region of the mean (100) +- Two standard error (2 x 2.5 = 5.0) -- this is 95 - 105.
- Understanding of the above (5), we now realize that if the unit of standard error is small, the region that we predict will be smaller or tighter. In other words, if the standard error value in the above example was 1.0 rather than 2.5. The guessing or predicting result would have been different (narrower). To make this long (:-)), with the 1.0 as the standard error and 100 as the mean of a sample, we can argue that (1) about 68% of the sample means will be found in the region of the mean (100) +- one standard error (1.0) -- this is 99 - 101; (2) about 95% of the sample means will be found in the region of the mean (100) +- two standard errors (2.0) -- this is 98 -- 102. Note here that the predicted region became tighter than the above example with standard error, 2.5.
- Now, how can we make this standard error small? See the formulae in the text book which gives you two different kinds of standard error calculation. One is for the standard error of the probability, the other is for the standard error of the mean.
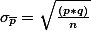 ,
,  . If we take a look at the two, we can argue that if the sample size gets bigger, the standard error value will be smaller. Or the upper parts get smaller, the standard error value will be smaller. The latter case should not be an issue here because... I mentioned this in my two articles -- please read them. The first case should be noted. That is, if sample size gets bigger the standard error value will be smaller.
. If we take a look at the two, we can argue that if the sample size gets bigger, the standard error value will be smaller. Or the upper parts get smaller, the standard error value will be smaller. The latter case should not be an issue here because... I mentioned this in my two articles -- please read them. The first case should be noted. That is, if sample size gets bigger the standard error value will be smaller.
- THEN, QUESTION: what does it mean by that "having a smaller sampling error value"?
ANSWER: I already explained this in 5 and 6.