ConditionalAccessSystem › ConfidenceInterval › ContactsInformation › Correlation › CoursesListbyAcademicYear › Covariance
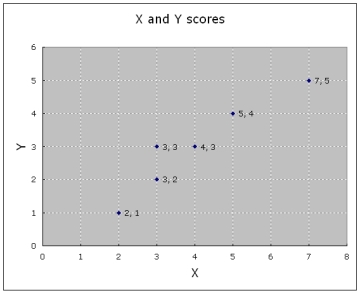
| X | Y | |
| 2 | 1 | |
| 3 | 2 | |
| 5 | 4 | |
| 3 | 3 | |
| 7 | 5 | |
| sum | 20 | 15 |
| mean | 4 | 3 |
| n | 5 | 5 |
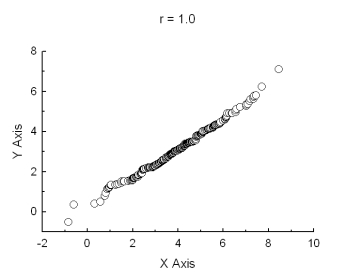
perfect
positive
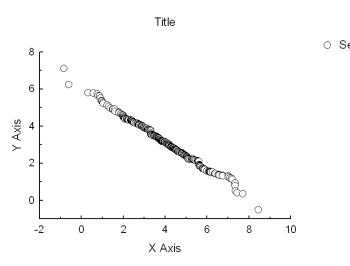
negative
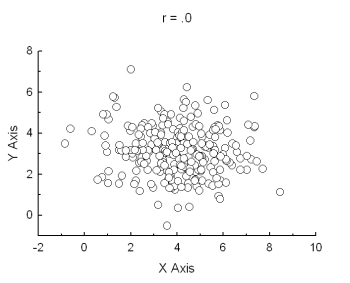
0
Covariance: X와 Y가 같이 변하는 정도
Var[X]: X의 구성원이 변하는 정도
Var[Y]: Y의 구성원이 변하는 정도
CovX,Y: X와 Y가 동시에 변하는 정도
`Var[X]=[sum(X_i-bar(X))^2]/n=[sum(X_i-bar(X))(X_i-bar(X))]/n=s_X^2`
`Var[Y]=[sum(Y_i-bar(Y))^2]/n=[sum(Y_i-bar(Y))(Y_i-bar(Y))]/n=s_Y^2`
`Cov[X,Y]=[sum(X_i-bar(X))(Y_i-bar(Y))]/n=s_(XY)`
Var[X]: X의 구성원이 변하는 정도
Var[Y]: Y의 구성원이 변하는 정도
CovX,Y: X와 Y가 동시에 변하는 정도
`Var[X]=[sum(X_i-bar(X))^2]/n=[sum(X_i-bar(X))(X_i-bar(X))]/n=s_X^2`
`Var[Y]=[sum(Y_i-bar(Y))^2]/n=[sum(Y_i-bar(Y))(Y_i-bar(Y))]/n=s_Y^2`
`Cov[X,Y]=[sum(X_i-bar(X))(Y_i-bar(Y))]/n=s_(XY)`
| X | Y | ds(X) | ds(Y) | ds(X)^2 | ds(Y)^2 | |||||||||
| 2 | 1 | -2 | -2 | 4 | 4 | |||||||||
| 3 | 2 | -1 | -1 | 1 | 1 | |||||||||
| 5 | 4 | 1 | 1 | 1 | 1 | |||||||||
| 3 | 3 | -1 | 0 | 1 | 0 | |||||||||
| 7 | 5 | 3 | 2 | 9 | 4 | . | mean | 4 | 3 | 16 | 10 | |||
| n | 5 | s^2 | 3.2 | 2 | ||||||||||
| s | 1.79 | 1.4 |
`s_(XY) = sum((X_i-bar(X))(Y_i-bar(Y)))/n` . . . . . 에서, 위의 분자만을 보면, `=> sum(X_iYi-X_ibar(Y)-Y_ibar(X)+bar(X)bar(Y))` `=> sum(X_iYi) - sum(X_ibar(Y)) - sum(Y_ibar(X)) + sum(bar(X)bar(Y))`. . . . . 에서 각 summation기호의 상수a는 na와 같이 변하므로 `=> sum(X_iYi) - bar(Y)sum(X_i) - bar(X)sum(Y_i) + n(bar(X)bar(Y))` `=> sum(X_iYi) - bar(Y) n bar(X) - bar(X) n bar(Y) + n(bar(X)bar(Y))` `=> sum(X_iYi) - n bar(X) bar(Y)` 따라서 `s_(XY) = [sum(X_iYi)]/n - bar(X) bar(Y)` |
또한,
`Var[X+a]=Var[X]` `Var[aX]=a^2*Var[X]` . . . . 와 마찬가지로 `Cov[X+a,Y+a]=Cov[X,Y]` `Cov[aX,aY]=a^2 Cov[X,Y]` |
마지막 식이 문제를 일으킴 . . . . 단위가 달라지면 Covariance amount (공변량)이 달라지는가. . . .
`rho_(XY) = sigma_(XY)/sigma_X sigma_Y`
`rho_(XY) = sigma_(XY)/sigma_X sigma_Y`
즉, 상관계수 로(rho)는 X,Y 각 변인의 공변량을 각 변인의 표준편차(sigma)로 나누어 준 값을 말한다. 위는 모집단일 경우이고 샘플에 관한 상관계수는
`r_(XY) = s_(XY)/s_X s_Y` . . . . 위의 데이터를 이용하여 r값을 구해보면
`r_(XY) = 2.4 / [1.79 * 1.414] = .949`
`r_(XY) = s_(XY)/s_X s_Y` . . . . 위의 데이터를 이용하여 r값을 구해보면
`r_(XY) = 2.4 / [1.79 * 1.414] = .949`
| X | Y | ds(X) | ds(Y) | ds(X)^2 | ds(Y)^2 | ds(XY) | ||
| 2 | 1 | -2 | -2 | 4 | 4 | 4 | ||
| 3 | 2 | -1 | -1 | 1 | 1 | 1 | ||
| 5 | 4 | 1 | 1 | 1 | 1 | 1 | ||
| 3 | 3 | -1 | 0 | 1 | 0 | 0 | ||
| 7 | 5 | 3 | 2 | 9 | 4 | 6 | ||
| mean | 4 | 3 | sum | 16 | 10 | sum | 12 | |
| n | 5 | s^2 | 3.2 | 2 | cov | 2.4 | ||
| s | 1.789 | 1.414 | ||||||
| r = covx,y/s[x]s[y] | 0.949 |
