No older revisions available
Correspondence analysis에 대해서 ¶
- 이 글은 아래의 페이퍼에 대한 질문에 답을 하기 위해서 작성되었습니다.
- 박한우, 한지은, 최경호, 김효동, Mirandilla, K.A. (2005, 10월 8일). 필리핀의 2004년 선거 웹사이트를 대상으로 한 웹 공간 분석. 한국언론학회 가을철 정기학술대회 발표집, pp. 441-471, 서울: 연세대학교.
- 아래의 데이터는 어느 한 회사 직원의 직급과 흡연을 정리한 것입니다. 회사에서의 개인의 직급과 흡연정도를 측정한 것입니다. 가설은 "직급이 낮을 수록 스테레스로 인하여 흡연량이 많아 질 것"입니다.
- 직급: 1: 초급; 2: 중급; 3:숙련; 4:고급
- 흡연: 1: 안핀다; 2: 조금핀다; 3: 보통정도 핀다; 4: 많이 핀다; 5: 매우 많이 핀다
| 직급 | 흡연 |
| 1 | 1 | 5 |
| 2 | 1 | 4 |
| 3 | 1 | 5 |
| 4 | 2 | 4 |
| 5 | 2 | 3 |
| 6 | 2 | 2 |
| 7 | 3 | 3 |
| 8 | 3 | 2 |
| 9 | 3 | 2 |
| 10 | 3 | 3 |
| 11 | 3 | 3 |
| 12 | 4 | 2 |
| 13 | 4 | 1 |
| 14 | 4 | 1 |
| 15 | 4 | 1 |
| 16 | 4 | 1 |
| 17 | 4 | 1 |
| 18 | 4 | 1 |
| 19 | 4 | 2 |
| 20 | 4 | 3 |
| 21 | 4 | 2 |
| 22 | 1 | 3 |
| 23 | 1 | 4 |
| 24 | 1 | 5 |
| 25 | 1 | 4 |
| 26 | 1 | 5 |
- 위의 데이터는 아래의 테이블과 같이 요약될 수 있습니다. 각 행,열의 Active Margin값은 해당행과 열의 합값을 나타내는 것으로 이것이 0이 된다면, 그것은 Active하지 않은 것으로 간주합니다. 그리고 이 active margin은 데이터의 CA에서 나타날 수 있는 차원(Dimension)을 구하는데 쓰입니다. 예를 들면, 위의 보기에서 데이터의 카테고리를 보면 4개, 5개의 카테고리입니다. 이 때, 모든 행과 열의 Active margin이 0이 아니면, 이 데이터의 최대 차원 수는 가장 작은 카테고리의 숫자에서 하나를 뺀 것이 됩니다(위의 경우, 3). 만약에 Active하지 않은 margin이 있다면, 그 숫자만큼 빼 주면 됩니다.
- 전체 빈도 수 (total)을 1로 단위화하여 다시 구한 숫자 (다음 표 참조)에서 각 Active margin의 숫자는 mass로 표현한다. 즉, mass는 contigency table을 전체적으로 단위화하는 것입니다.
- contigency table을 전체 case의 합을 1로 보는 비율로 환산한다는 이야기는 비율을 이용하여 CA를 행해도 큰 무리가 없다는 이야기입니다.
- 또한 각 셀에 0이 있어도 무리가 없습니다. 어느 한 행이나 열의 모든 셀이 0인 경우에는 예상가능한 전체 dimension의 숫자를 하나 빼주면 되는 것으로 알고 있습니다.
- intertia는 centroid 값에서의 제곱값의 거리와 mass값의 함수로 나타내는데, CA의 경우에는 주로 Pearson 의 Chisqure값을 전체 빈도수(26)로 나눈 값을 말합니다. CA는 전체적인 Chisquare 값을 구한 후, 이 값에서 각 intertia가 이에 부분적으로 얼마나 영향을 주는 지를 나타내 준다는 방법으로 원리는 factor analysis와 비슷합니다. 단지 FA는 ratio 측정에서 할 수 있으며, CA는 frequency 측정에서 할 수 있습니다 (적어도 바람직 합니다).
| Correspondence Table | | | | | | |
| man | drink | | | | | | | | |
| 안핀다 | 조금 핀타 | 보통이다 | 많이 핀다 | 매우 많이 핀다 | Active Margin |
| 초급 | 0 | 0 | 1 | 3 | 4 | 8 |
| 중급 | 0 | 1 | 1 | 1 | 0 | 3 |
| 숙련 | 0 | 2 | 3 | 0 | 0 | 5 |
| 고급 | 6 | 3 | 1 | 0 | 0 | 10 |
| Active Margin | 6 | 6 | 6 | 4 | 4 | 26 |
| Correspondence Table | |
| man | drink | |
| 안핀다 | 조금핀다 | 보통이다 | 많이 핀다 | 매우 많이 핀다 | Active Margin |
| 초급 | 0.000 | 0.000 | 0.038 | 0.115 | 0.154 | 0.308 |
| 중급 | 0.000 | 0.038 | 0.038 | 0.038 | 0.000 | 0.115 |
| 숙련 | 0.000 | 0.077 | 0.115 | 0.000 | 0.000 | 0.192 |
| 고급 | 0.231 | 0.115 | 0.038 | 0.000 | 0.000 | 0.385 |
| Active Margin | 0.231 | 0.231 | 0.231 | 0.154 | 0.154 | 1.000 |
- 사실 위의 표는 row와 column을 한꺼번에 처리하였지만, 개개는 Row와 Column을 각기 처리하여 각각의 평균 mass와 intertia를 구하여 그 카테고리가 얼마나 다른지를 알아보게 됩니다. 즉, 위의 Active margin 값은 행과 열을 독립적으로 생각하고 구한 후에, 이에 대한 거리(eucledian distance) 혹은 Chi-square와 같이 expected value에서 얼마나 벗어나 있는지를 측정하여, 각 카테고리의 상대적인 위치를 구하게 됩니다. 이런 위치 차이의 중요도는 centroid에서 각각의 카테고리가 얼마나 벗어나 있는지를 재는 (integral (mass)/(distance(from centroid))^2, CA의 경우) inertia값에 의해서 판단하게 됩니다.
- 아래의 테이블은 row와 column profile에서 추출한 정보입니다.
| Overview Row Points(a) |
| man | Mass | Score in Dimension | Inertia | Contribution | |
| | 1 | 2 | | Of Point to Inertia of Dimension | Of Dimension to Inertia of Point |
| | | | | 1 | 2 | 1 | 2 | Total |
| 초급 | 0.31 | 1.31 | -0.36 | 0.49 | 0.60 | 0.07 | 0.95 | 0.05 | 1.00 |
| 중급 | 0.12 | 0.17 | 0.76 | 0.08 | 0.00 | 0.11 | 0.04 | 0.51 | 0.54 |
| 숙련 | 0.19 | -0.34 | 1.35 | 0.24 | 0.03 | 0.58 | 0.08 | 0.88 | 0.96 |
| 고급 | 0.38 | -0.93 | -0.61 | 0.38 | 0.37 | 0.24 | 0.77 | 0.23 | 1.00 |
| Active Total | 1 | | | 1.20 | 1 | 1 | |
| a: Symmetrical normalization | Overview Row Points(a) |
| smoke | Mass | Score in Dimension | Inertia | Contribution | |
| | 1 | 2 | | Of Point to Inertia of Dimension | Of Dimension to Inertia of Point |
| | | | | 1 | 2 | 1 | 2 | Total |
| 안핀다 | 0.23 | -1.05 | -1.02 | 0.37 | 0.29 | 0.40 | 0.61 | 0.39 | 1.00 |
| 조금핀다 | 0.23 | -0.62 | 0.45 | 0.11 | 0.10 | 0.08 | 0.73 | 0.26 | 0.99 |
| 보통이다 | 0.23 | -0.09 | 1.06 | 0.16 | 0.00 | 0.43 | 0.01 | 0.96 | 0.97 |
| 많이핀다 | 0.15 | 1.16 | -0.14 | 0.21 | 0.23 | 0.00 | 0.87 | 0.01 | 0.87 |
| 매우많이 | 0.15 | 1.48 | -0.60 | 0.35 | 0.38 | 0.09 | 0.86 | 0.10 | 0.96 |
| Active Total | 1 | | | 1.20 | 1 | 1 | |
| a: Symmetrical normalization |
- 각각의 scores in dimension에서 구한 정보를 2차원의 도표에 정리를 하면 총체적인 행과 열 각각의 위치를 도식화할 수 있습니다. 그러나, 대개는 2개 변수를 한 도표에 표시하여 도식화 합니다. 아래는 그 결과입니다.
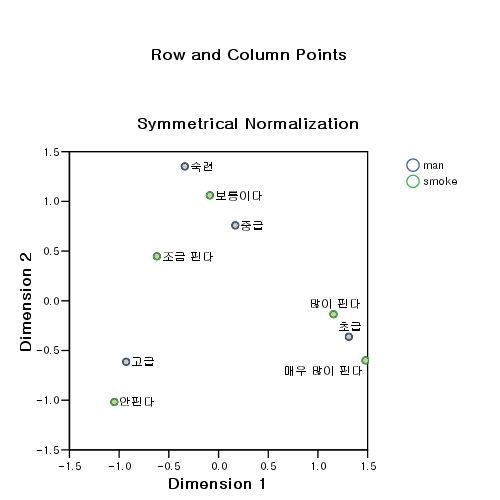
[JPG image (36.27 KB)]
- CA의 assumption으로 첫 째는 이 방법이 expoloratory하다는 것입니다. Chi-square값을 보는 것은 단지 이를 기준으로 각 margin들이 거리를 두는가를 체크하기 위한 것입니다. 따라서 significance test는 없습니다. 꼭 significance test를 해야 한다면 다른 방법을 쓰는 것으로 알고 있습니다 (e.g., log-linear).
- 각 행과 열이 독립적인 것이 inertia를 읽는데 도움을 줍니다. 사실, 완전 독립성이라면, 각 profile의 mass value만으로도 각 셀의 값을 구할 수 있습니다 (논문에서 문제시가 되어야 한다면 이 부분입니다).
- Chi-square가 가지는 성격인 non-parametic 테스트입니다. normal distribution과 상관 없습니다. 또한 갯수를 세는 것이므로 셀값이 마이너스 여서는 안됩니다.
- CA는 보통 많은 category를 가진 두 세개의 variables을 가지고 합니다.