FrontPage › AnalyzingSocialNetworks_Borgatti
Contents
- 1. 1 Introduction
- 2. 2 Mathematical Foundations
- 3. 3 Research Design
- 4. 4 Data Collection
- 5. 5 Data Management
- 6. 6 Multivariate Techniques Used in Network Analysis
- 7. 7 Visualization
- 8. 8 Testing Hypotheses
- 9. 9 Characterizing Whole Networks
- 10. 10 Centrality
- 11. 11 Subgroups
- 12. 12 Equivalence
- 13. 13 Analyzing Two-Mode Data
- 14. 14 Large Networks
- 15. 15 Ego Networks
- 16. References
- 17. Index
Preface
5. 5 Data Management ¶
Data management:
----
----
 UCINET_6_Users_Guide.docx (96.48 KB)
UCINET_6_Users_Guide.docx (96.48 KB)
 Entering Data Using the DL Editor.docx (432.31 KB)
Entering Data Using the DL Editor.docx (432.31 KB)
Learning Outcomes
- Configure network and attribute data for standard software packages
- Apply elementary transformations to matrix data
- Extract and reconfigure network and attribute data
5.1. Introduction ¶
We will discuss:
![[https]](/imgs/https.png) UCINET.
UCINET.
- how to format network data for import into a network analysis software package,
- how to transform network data to make it suitable for different analyses, and
- how to export network data and results for use in other programs.
![[https]](/imgs/https.png) UCINET.
UCINET. 5.2. Data import ¶
For most users, we recommend using Microsoft Excel as a sort of universal translator (or any kind of spreadsheet program).
And DL format (data language)
UCINET tackles various format such as . . .
- matrix format
- list format
- Nodelist
- Edgelist
- Nodelist
5.2.2. List formats ¶
- matrix format takes a lot of space in terms of memory and disk.
- Indicating the only relations among the network nodes may be more efficient.
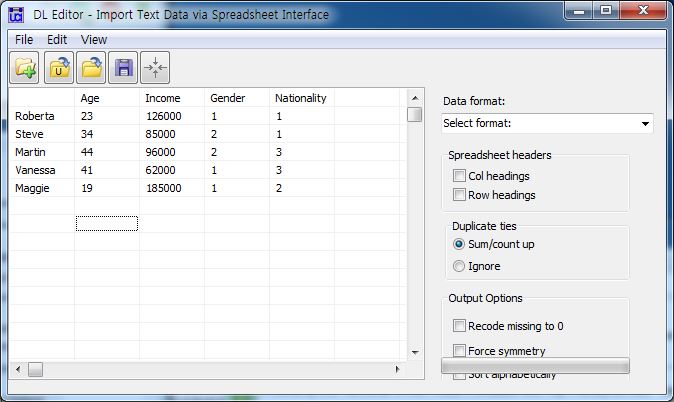
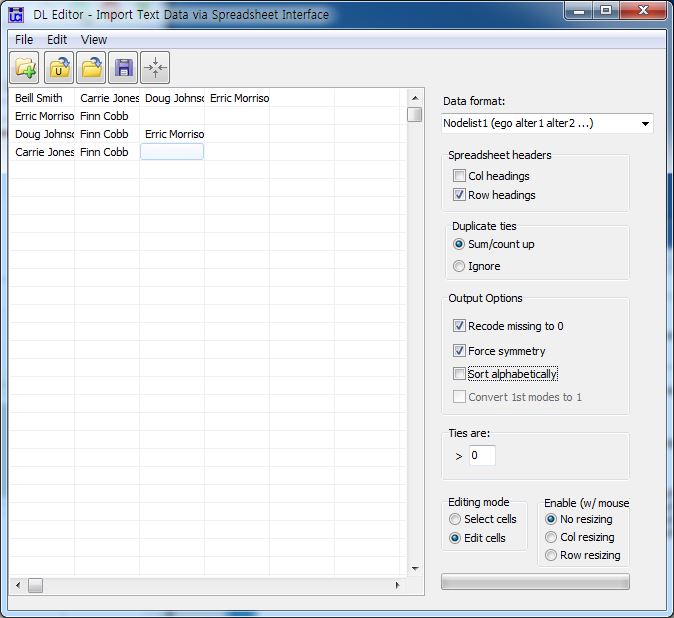
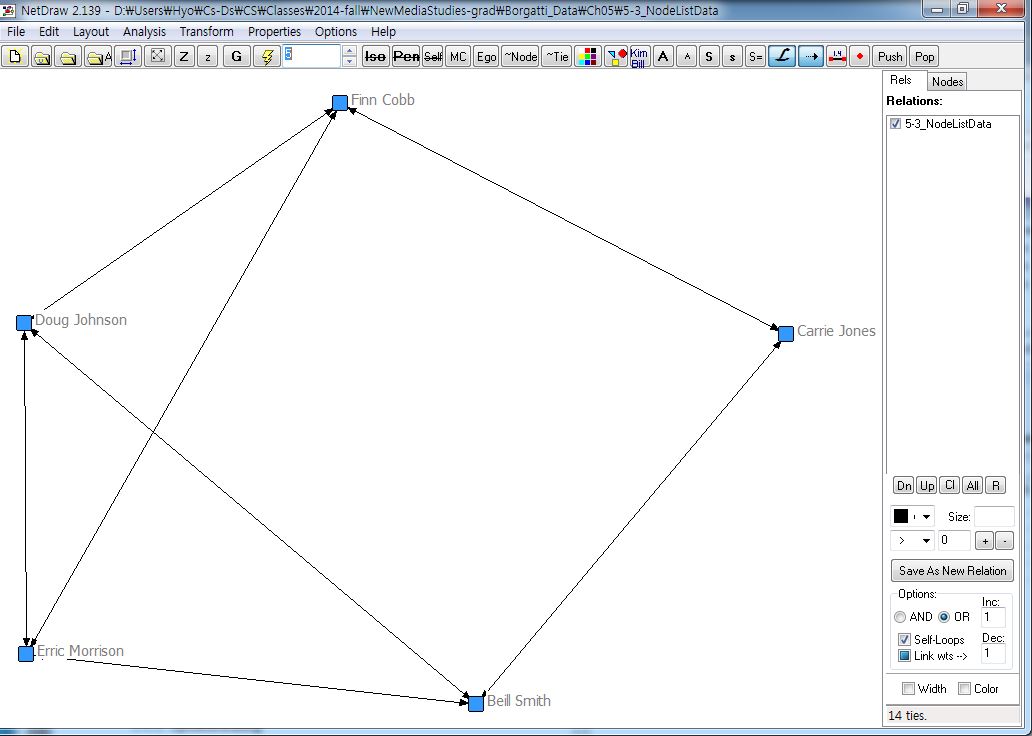
5.2.2.1. Nodelist ¶
 [JPG image (69.46 KB)] |
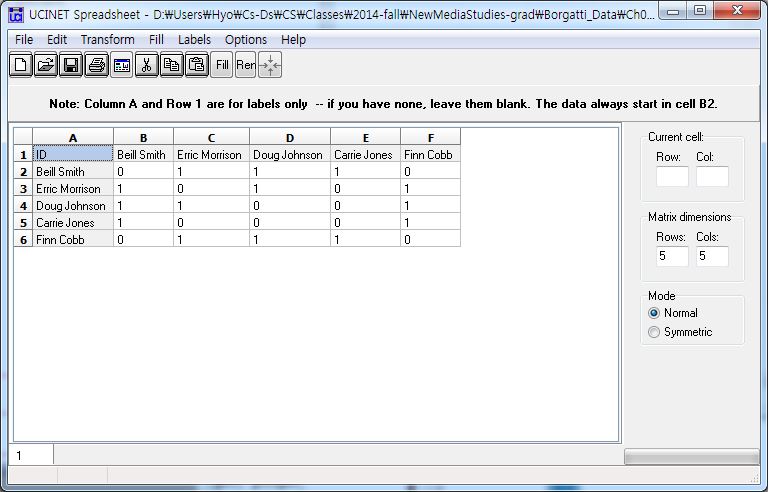
DL N=5 FORMAT = FULLMATRIX DIAGONAL PRESENT SYMMETRIC = YES LABELS embedded DATA: "Beill Smith" "Carrie Jones" "Doug Johnson" "Erric Morrison" "Erric Morrison" "Finn Cobb" "Doug Johnson" "Finn Cobb" "Erric Morrison" "Carrie Jones" "Finn Cobb"
 [JPG image (66.1 KB)] |
 [JPG image (80.2 KB)] |  5-3_NodeListData2.txt (255 Bytes) OR 5-3_NodeListData2.txt (255 Bytes) OR 5-3_NodeListData.txt (749 Bytes) 5-3_NodeListData.txt (749 Bytes) |
| Two mode data |  5-6_TwoModeNodelistDlFile.txt (176 Bytes) 5-6_TwoModeNodelistDlFile.txt (176 Bytes) |
DL nr=3, nc=5 format=nodelist2 row labels embedded column labels embedded data: George, Darts, Pool, Dancing Sue, Dancing, Volleyball Sally, Dancing, Darts, Basketball
5.2.2.2. Edgelist ¶
Each row has two columns indicating the pair of nodes that have the tie. Optionally, a third column can be included which gives the strength of the tie. . . .
| Node1 | Node2 |
| Node1 | Node2 | 3 |
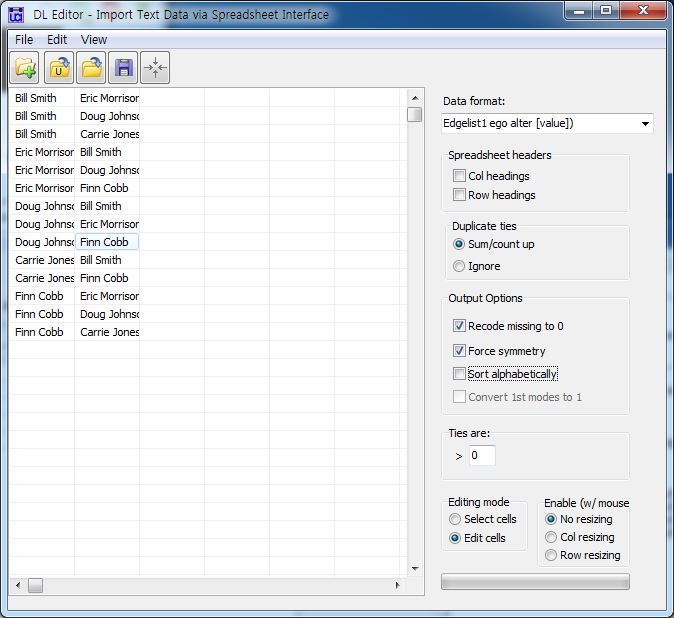
[JPG image (75.92 KB)]
[JPG image (124.18 KB)]
5.3. Cleaning network data ¶
- Be careful:
replicated actor
missing actor
- Data characteristics
had lunch with . . . . data should be symmetric.
What do you do about it?
- Take a look at isolates.
- Ethnographic hunch . . . Who's gonna be the center . . . Make a quick picture of the data.
5.4. Data transformation ¶
- transposing matrices,
- symmetrizing,
- dichotomizing,
- imputing missing values,
- combining relations,
- combining nodes,
- extracting subgraphs, and many more.
- Permute: Re-order rows, columns or matrices in a dataset according to a user specified list.
- bipartite: Convert a 2-mode dataset into a 1-mode adjacency matrix
- Any 2-mode incidence matrix can be thought of as a bipartite graph. If the 2-modes are actors and events then the bipartite graph consists of the union of the actors and events as vertices with the edges only connecting actors with events (ie no connections between actors or between events). This routine takes a 2-mode incidence matrix and converts it to a 1-mode adjacency matrix of a bipartite graph. If the incidence matrix had n rows and m columns then the resultant adjacency matrix would be a square matrix of dimension m+n.
- Any 2-mode incidence matrix can be thought of as a bipartite graph. If the 2-modes are actors and events then the bipartite graph consists of the union of the actors and events as vertices with the edges only connecting actors with events (ie no connections between actors or between events). This routine takes a 2-mode incidence matrix and converts it to a 1-mode adjacency matrix of a bipartite graph. If the incidence matrix had n rows and m columns then the resultant adjacency matrix would be a square matrix of dimension m+n.
5.4.1. Transposing ¶
- To interchange its rows with its columns
- When the matrix is non-symmetric, it makes relationships reversed. (Transposing an adjacency matrix is equivalent to reversing the direction of the arrows.)
- by suvey's nature, it becomes very useful.
- 'who do you seek advice from?' : the constructed data should be transposed:
- food webs, too.
- which species eat which species?
- whose energy flow to whom? = The matrix is transposed by ecologist.
- which species eat which species?
- 'who do you seek advice from?' : the constructed data should be transposed:
- row x col x layers
- row - col
- row - layer
- col - layer
- row - col
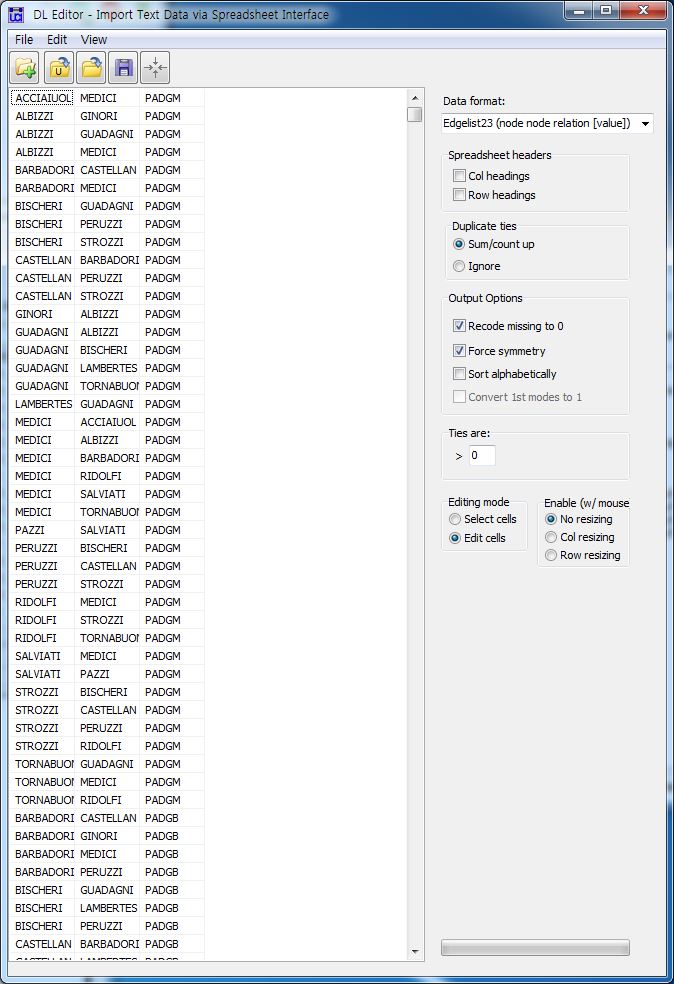
- Padgett dataset: marriage and business ties among Florentine families during the Renaissance period.
DL N=16 NM=2 FORMAT = FULLMATRIX DIAGONAL PRESENT ROW LABELS: "ACCIAIUOL" "ALBIZZI" "BARBADORI" "BISCHERI" "CASTELLAN" "GINORI" "GUADAGNI" "LAMBERTES" "MEDICI" "PAZZI" "PERUZZI" "PUCCI" "RIDOLFI" "SALVIATI" "STROZZI" "TORNABUON" COLUMN LABELS: "ACCIAIUOL" "ALBIZZI" "BARBADORI" "BISCHERI" "CASTELLAN" "GINORI" "GUADAGNI" "LAMBERTES" "MEDICI" "PAZZI" "PERUZZI" "PUCCI" "RIDOLFI" "SALVIATI" "STROZZI" "TORNABUON" LEVEL LABELS: "PADGM" "PADGB" DATA: 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
- centrality measure
MULTIPLE CENTRALITY MEASURES -------------------------------------------------------------------------------- Input dataset: PADGETT (D:\Users\Hyo\Cs-Ds\CS\Classes\2014-fall\NewMediaStudies-grad\Borgatti_Data\Ch05\PADGETT) Output dataset: PADGETT-cent (D:\Users\Hyo\Cs-Ds\CS\Classes\2014-fall\NewMediaStudies-grad\Borgatti_Data\Ch05\PADGETT-cent) Treat data as: Auto-detect Type of scores to output: Raw scores Undefined dist in closeness: replace with max dist + 1 Network PADGM is directed? NO Value of Beta was: 0.305579943942584 Network PADGB is directed? NO Value of Beta was: 0.300228499969756 Centrality Measures PADGM 1 2 3 4 5 6 7 8 9 Degree 2local BonPwr 2Step ARD Closene Eigenve Between 2StepBe ------- ------- ------- ------- ------- ------- ------- ------- ------- 1 ACCIAIUOL 1.000 6.000 301.290 6.000 5.917 44.000 0.132 0.000 0.000 2 ALBIZZI 3.000 11.000 557.416 10.000 7.833 35.000 0.244 19.333 2.500 3 BARBADORI 2.000 9.000 482.693 9.000 7.083 38.000 0.212 8.500 1.000 4 BISCHERI 3.000 11.000 644.632 8.000 7.200 41.000 0.283 9.500 2.000 5 CASTELLAN 3.000 9.000 590.363 6.000 6.917 42.000 0.259 5.000 2.000 6 GINORI 1.000 3.000 171.335 3.000 5.333 48.000 0.075 0.000 0.000 7 GUADAGNI 4.000 10.000 660.285 9.000 8.083 36.000 0.289 23.167 5.500 8 LAMBERTES 1.000 4.000 202.770 4.000 5.367 49.000 0.089 0.000 0.000 9 MEDICI 6.000 14.000 982.689 11.000 9.500 31.000 0.430 47.500 13.500 10 PAZZI 1.000 2.000 102.991 2.000 4.767 55.000 0.045 0.000 0.000 11 PERUZZI 3.000 10.000 628.266 6.000 6.783 44.000 0.276 2.000 0.500 12 PUCCI 0.000 0.000 -0.000 0.000 0.000 90.000 0.000 0.000 0.000 13 RIDOLFI 3.000 13.000 778.167 11.000 8.000 34.000 0.342 10.333 2.000 14 SALVIATI 2.000 7.000 333.762 7.000 6.583 42.000 0.146 13.000 1.000 15 STROZZI 4.000 12.000 811.167 8.000 7.833 38.000 0.356 9.333 3.500 16 TORNABUON 3.000 13.000 742.852 10.000 7.833 35.000 0.326 8.333 1.500 PADGB 1 2 3 4 5 6 7 8 9 Degree 2local BonPwr 2Step ARD Closene Eigenve Between 2StepBe ------- ------- ------- ------- ------- ------- ------- ------- ------- 1 ACCIAIUOL 0.000 0.000 0.000 0.000 0.000 90.000 0.000 0.000 0.000 2 ALBIZZI 0.000 0.000 0.000 0.000 0.000 90.000 0.000 0.000 0.000 3 BARBADORI 4.000 14.000 756.242 9.000 6.833 47.000 0.390 25.000 4.000 4 BISCHERI 3.000 10.000 663.468 5.000 5.417 55.000 0.344 2.500 0.500 5 CASTELLAN 3.000 12.000 754.534 7.000 6.000 50.000 0.391 5.000 0.500 6 GINORI 2.000 9.000 370.702 7.000 5.417 52.000 0.191 0.000 0.000 7 GUADAGNI 2.000 7.000 452.922 4.000 4.433 62.000 0.235 0.000 0.000 8 LAMBERTES 4.000 12.000 838.463 5.000 5.917 54.000 0.435 6.000 2.000 9 MEDICI 5.000 9.000 471.830 7.000 6.917 49.000 0.241 24.000 9.000 10 PAZZI 1.000 5.000 142.657 5.000 4.367 58.000 0.073 0.000 0.000 11 PERUZZI 4.000 14.000 908.501 7.000 6.500 49.000 0.471 13.500 2.000 12 PUCCI 0.000 0.000 0.000 0.000 0.000 90.000 0.000 0.000 0.000 13 RIDOLFI 0.000 0.000 0.000 0.000 0.000 90.000 0.000 0.000 0.000 14 SALVIATI 1.000 5.000 142.657 5.000 4.367 58.000 0.073 0.000 0.000 15 STROZZI 0.000 0.000 0.000 0.000 0.000 90.000 0.000 0.000 0.000 16 TORNABUON 1.000 5.000 142.657 5.000 4.367 58.000 0.073 0.000 0.000 ---------------------------------------- Running time: 00:00:01 Output generated: 29 9 14 16:41:40 UCINET 6.511 Copyright (c) 1992-2012 Analytic Technologies
[1] Degree
1 2
P P
- -
1 ACCIAIUOL 1 0
2 ALBIZZI 3 0
3 BARBADORI 2 4
4 BISCHERI 3 3
5 CASTELLAN 3 3
6 GINORI 1 2
7 GUADAGNI 4 2
8 LAMBERTES 1 4
9 MEDICI 6 5
10 PAZZI 1 1
11 PERUZZI 3 4
12 PUCCI 0 0
13 RIDOLFI 3 0
14 SALVIATI 2 1
15 STROZZI 4 0
16 TORNABUON 3 1
[2] 2local
1 2
PA PA
-- --
1 ACCIAIUOL 6 0
2 ALBIZZI 11 0
3 BARBADORI 9 14
4 BISCHERI 11 10
5 CASTELLAN 9 12
6 GINORI 3 9
7 GUADAGNI 10 7
8 LAMBERTES 4 12
9 MEDICI 14 9
10 PAZZI 2 5
11 PERUZZI 10 14
12 PUCCI 0 0
13 RIDOLFI 13 0
14 SALVIATI 7 5
15 STROZZI 12 0
16 TORNABUON 13 5
[3] BonPwr
1 2
PADGM PADGB
------- -------
1 ACCIAIUOL 301.290 0.000
2 ALBIZZI 557.416 0.000
3 BARBADORI 482.693 756.242
4 BISCHERI 644.632 663.468
5 CASTELLAN 590.363 754.534
6 GINORI 171.335 370.702
7 GUADAGNI 660.285 452.922
8 LAMBERTES 202.770 838.463
9 MEDICI 982.689 471.830
10 PAZZI 102.991 142.657
11 PERUZZI 628.266 908.501
12 PUCCI -0.000 0.000
13 RIDOLFI 778.167 -0.000
14 SALVIATI 333.762 142.657
15 STROZZI 811.167 0.000
16 TORNABUON 742.852 142.657
[4] 2Step
1 2
PA PA
-- --
1 ACCIAIUOL 6 0
2 ALBIZZI 10 0
3 BARBADORI 9 9
4 BISCHERI 8 5
5 CASTELLAN 6 7
6 GINORI 3 7
7 GUADAGNI 9 4
8 LAMBERTES 4 5
9 MEDICI 11 7
10 PAZZI 2 5
11 PERUZZI 6 7
12 PUCCI 0 0
13 RIDOLFI 11 0
14 SALVIATI 7 5
15 STROZZI 8 0
16 TORNABUON 10 5
[5] ARD
1 2
PADGM PADGB
----- -----
1 ACCIAIUOL 5.917 0.000
2 ALBIZZI 7.833 0.000
3 BARBADORI 7.083 6.833
4 BISCHERI 7.200 5.417
5 CASTELLAN 6.917 6.000
6 GINORI 5.333 5.417
7 GUADAGNI 8.083 4.433
8 LAMBERTES 5.367 5.917
9 MEDICI 9.500 6.917
10 PAZZI 4.767 4.367
11 PERUZZI 6.783 6.500
12 PUCCI 0.000 0.000
13 RIDOLFI 8.000 0.000
14 SALVIATI 6.583 4.367
15 STROZZI 7.833 0.000
16 TORNABUON 7.833 4.367
[6] Closeness
1 2
PA PA
-- --
1 ACCIAIUOL 44 90
2 ALBIZZI 35 90
3 BARBADORI 38 47
4 BISCHERI 41 55
5 CASTELLAN 42 50
6 GINORI 48 52
7 GUADAGNI 36 62
8 LAMBERTES 49 54
9 MEDICI 31 49
10 PAZZI 55 58
11 PERUZZI 44 49
12 PUCCI 90 90
13 RIDOLFI 34 90
14 SALVIATI 42 58
15 STROZZI 38 90
16 TORNABUON 35 58
[7] Eigenvector
1 2
PADGM PADGB
------ ------
1 ACCIAIUOL 0.132 0.000
2 ALBIZZI 0.244 0.000
3 BARBADORI 0.212 0.390
4 BISCHERI 0.283 0.344
5 CASTELLAN 0.259 0.391
6 GINORI 0.075 0.191
7 GUADAGNI 0.289 0.235
8 LAMBERTES 0.089 0.435
9 MEDICI 0.430 0.241
10 PAZZI 0.045 0.073
11 PERUZZI 0.276 0.471
12 PUCCI 0.000 -0.000
13 RIDOLFI 0.342 0.000
14 SALVIATI 0.146 0.073
15 STROZZI 0.356 -0.000
16 TORNABUON 0.326 0.073
[8] Between
1 2
PADGM PADGB
------ ------
1 ACCIAIUOL 0.000 0.000
2 ALBIZZI 19.333 0.000
3 BARBADORI 8.500 25.000
4 BISCHERI 9.500 2.500
5 CASTELLAN 5.000 5.000
6 GINORI 0.000 0.000
7 GUADAGNI 23.167 0.000
8 LAMBERTES 0.000 6.000
9 MEDICI 47.500 24.000
10 PAZZI 0.000 0.000
11 PERUZZI 2.000 13.500
12 PUCCI 0.000 0.000
13 RIDOLFI 10.333 0.000
14 SALVIATI 13.000 0.000
15 STROZZI 9.333 0.000
16 TORNABUON 8.333 0.000
[9] 2StepBet
1 2
PADGM PADGB
------ ------
1 ACCIAIUOL 0.000 0.000
2 ALBIZZI 2.500 0.000
3 BARBADORI 1.000 4.000
4 BISCHERI 2.000 0.500
5 CASTELLAN 2.000 0.500
6 GINORI 0.000 0.000
7 GUADAGNI 5.500 0.000
8 LAMBERTES 0.000 2.000
9 MEDICI 13.500 9.000
10 PAZZI 0.000 0.000
11 PERUZZI 0.500 2.000
12 PUCCI 0.000 0.000
13 RIDOLFI 2.000 0.000
14 SALVIATI 1.000 0.000
15 STROZZI 3.500 0.000
16 TORNABUON 1.500 0.000
----------------------------------------
Running time: 00:00:01
Output generated: 29 9 14 16:45:18
5.4.2. Imputing missing data ¶
Missing data
- Getting rid of the actor by deleting both row and the corresponding column)
- In case of symmetric or undirected relations.
5.4.3. Symmetrizing ¶
- Who do you communicate with whom?
- asymmetric matrix . . .
- by union rule (or OR rule)
5.4.4. Dichotomizing ¶
- For very practical reason
- some methods, especially graph-theoretic methods, are only applicable to binary data.
- Also, dichotomizing with a high cut-off can serve to reduce the density of the network, which is useful in handling large networks
- some methods, especially graph-theoretic methods, are only applicable to binary data.
- it is usually advisable to dichotomize at different levels ???
5.4.5. Combining relations ¶
- who do you attend sports events with?
- who do you go to the theatre with?, and
- who do you go out to dinner with?
- combine them into a more general, analytically defined, relation, such as
- who socialized with whom?
- who socialized with whom?
- Sampson dataset
- Transform - Matrix Operation - Aggregation
- Use add method.
- Correlations between relations
SIMILARITIES -------------------------------------------------------------------------------- Measure: CORRELATION Variables are: MATRICES Diagonal: TREATED AS MISSING Input dataset: sampson (D:\Users\Hyo\Cs-Ds\CS\Classes\2014-fall\NewMediaStudies-grad\Borgatti_Data\Ch05\Sampson-Samplk\sampson) Similarity matrix: sampson-Sim (D:\Users\Hyo\Cs-Ds\CS\Classes\2014-fall\NewMediaStudies-grad\Borgatti_Data\Ch05\Sampson-Samplk\sampson-Sim) 1 2 3 4 5 6 7 8 9 10 SAMPLK SAMPLK SAMPLK SAMPDL SAMPES SAMPDE SAMPIN SAMPNI SAMPPR SAMPNP ------ ------ ------ ------ ------ ------ ------ ------ ------ ------ 1 SAMPLK1 1.000 0.645 0.638 -0.103 0.510 -0.146 0.530 -0.149 0.384 -0.011 2 SAMPLK2 0.645 1.000 0.768 -0.149 0.633 -0.167 0.616 -0.166 0.508 -0.087 3 SAMPLK3 0.638 0.768 1.000 -0.168 0.653 -0.176 0.651 -0.165 0.554 -0.055 4 SAMPDLK -0.103 -0.149 -0.168 1.000 -0.145 0.689 -0.113 0.522 -0.136 0.340 5 SAMPES 0.510 0.633 0.653 -0.145 1.000 -0.186 0.797 -0.171 0.629 -0.141 6 SAMPDES -0.146 -0.167 -0.176 0.689 -0.186 1.000 -0.142 0.660 -0.148 0.425 7 SAMPIN 0.530 0.616 0.651 -0.113 0.797 -0.142 1.000 -0.170 0.642 -0.151 8 SAMPNIN -0.149 -0.166 -0.165 0.522 -0.171 0.660 -0.170 1.000 -0.141 0.355 9 SAMPPR 0.384 0.508 0.554 -0.136 0.629 -0.148 0.642 -0.141 1.000 -0.125 10 SAMPNPR -0.011 -0.087 -0.055 0.340 -0.141 0.425 -0.151 0.355 -0.125 1.000 Cronbach's Alpha = 0.710 Similarity matrix saved as dataset sampson-Sim ---------------------------------------- Running time: 00:00:01 Output generated: 29 9 14 17:38:15 UCINET 6.511 Copyright (c) 1992-2012 Analytic Technologies
- Then do factor analysis
FACTOR ANALYSIS -------------------------------------------------------------------------------- Method of extraction: PRINCIPAL COMPONENTS Method of rotation: VARIMAX Minimum eigenvalue to retain: 1 Data type: 1-mode correlation matrix Input dataset: sampson-Sim (D:\Users\Hyo\Cs-Ds\CS\Classes\2014-fall\NewMediaStudies-grad\Borgatti_Data\Ch05\Sampson-Samplk\sampson-Sim) EIGENVALUES FACTOR VALUE PERCENT CUM % RATIO ------- -------- ------- ------- ------- 1: 4.33185 43.3 43.3 1.913 2: 2.26442 22.6 66.0 2.722 3: 0.83177 8.3 74.3 1.310 4: 0.63496 6.3 80.6 1.301 5: 0.48813 4.9 85.5 1.249 6: 0.39076 3.9 89.4 1.067 7: 0.36615 3.7 93.1 1.356 8: 0.26992 2.7 95.8 1.181 9: 0.22847 2.3 98.1 1.180 10: 0.19356 1.9 100.0 ======= ======== ======= ======= ======= 10.00000 100.0 Unrotated Factor Loadings 1 2 ------ ------ 1 SAMPLK1 0.710 0.231 2 SAMPLK2 0.817 0.227 3 SAMPLK3 0.836 0.235 4 SAMPDLK -0.373 0.732 5 SAMPES 0.835 0.206 6 SAMPDES -0.422 0.790 7 SAMPIN 0.830 0.233 8 SAMPNIN -0.400 0.706 9 SAMPPR 0.724 0.179 10 SAMPNPR -0.272 0.564 Rotated Factor Loadings 1 2 ------ ------ 1 SAMPLK1 0.745 -0.046 2 SAMPLK2 0.844 -0.089 3 SAMPLK3 0.864 -0.088 4 SAMPDLK -0.078 0.818 5 SAMPES 0.852 -0.115 6 SAMPDES -0.102 0.889 7 SAMPIN 0.858 -0.088 8 SAMPNIN -0.113 0.804 9 SAMPPR 0.739 -0.099 10 SAMPNPR -0.046 0.624 Eigenvalues saved as dataset Eigen (D:\Users\Hyo\Cs-Ds\CS\Classes\2014-fall\NewMediaStudies-grad\Borgatti_Data\Ch05\Sampson-Samplk\Eigen) Factor loadings saved as dataset Loadings (D:\Users\Hyo\Cs-Ds\CS\Classes\2014-fall\NewMediaStudies-grad\Borgatti_Data\Ch05\Sampson-Samplk\Loadings) ---------------------------------------- Running time: 00:00:01 Output generated: 29 9 14 17:37:04 UCINET 6.511 Copyright (c) 1992-2012 Analytic Technologies
Rotated Factor Loadings 1 2 ------ ------ 3 SAMPLK3 0.864 -0.088 7 SAMPIN 0.858 -0.088 5 SAMPES 0.852 -0.115 2 SAMPLK2 0.844 -0.089 1 SAMPLK1 0.745 -0.046 9 SAMPPR 0.739 -0.099 ------------------------- 10 SAMPNPR -0.046 0.624 4 SAMPDLK -0.078 0.818 6 SAMPDES -0.102 0.889 8 SAMPNIN -0.113 0.804
- Transform - Matrix Operation - Aggregation
- Aggregating them accordingly (two different matrix, positive and negative). Then analyze them accordingly.
- . . . .
5.4.6. Combining nodes ¶
- who collaborates with whom in an organization, but what we are really interested in is the pattern of ties between departments . . .
- But, how?????
5.6. Cognitive social structure data ¶
True network
Network reality == Network in one's mind
Q: How would you measure the first one?
Q: How would you measure the first one?
- 'row-dominated locally aggregated structure' (RLAS)
- TRUST network
- (i, i, j) i's as in a row word taken as truth.
- TRUST network
- Intersection method (Intersected locally aggregated structure (ILAS)
- (i, i, j) =\= (j, i, j)
- (i, i, j) = 1 | (j, i, j) = 1 ==> (i, j) = 1
- (i, i, j) =\= (j, i, j)
- Consensus type
- R = (k, i, j) = ? When, a certain portion agrees, R has a value.
- R = (k, i, j) = ? When, a certain portion agrees, R has a value.
5.7. Matching attributes and networks ¶
M x M matrix data and
M x N (attributes) data
--> DATA -> Match Multiple Datasets
M x N (attributes) data
For example, if the data consists of Matrices 5.8 (a network) and 5.9 (an attribute matrix), an analysis that uses the network and the attribute data together (incorrectly) assumes that the person in the second row of the network matrix (Jeff) is female, because the second person in the attribute matrix is female.
. . . needs to take steps to ensure their attribute datasets are properly matched to their network datasets
--> DATA -> Match Net and Attrib datasets. . . needs to take steps to ensure their attribute datasets are properly matched to their network datasets
--> DATA -> Match Multiple Datasets
5.9. Data export ¶
Newfrat dataset
15 point time series one mode network data
extracting the node's centrality for each time set.
M x N x t(15), N = centrality measures (ratio, interval)
converting M*15 x N, data ->
newmat = appendasrows('newmat-cent')
15 point time series one mode network data
extracting the node's centrality for each time set.
M x N x t(15), N = centrality measures (ratio, interval)
converting M*15 x N, data ->
newmat = appendasrows('newmat-cent')
Or
x = appendasrows(transpose(newfrat-cent))
xT = transpose(x)
x = appendasrows(transpose(newfrat-cent))
xT = transpose(x)
xT becomes a dataset with repeated measures. . . . (t = 1, 15)
6. 6 Multivariate Techniques Used in Network Analysis ¶
Data used:  CITIES.zip (492 Bytes)
CITIES.zip (492 Bytes)
 CITIES.zip (492 Bytes)
CITIES.zip (492 Bytes)Learning outcomes
- Represent one- and two-mode data in a two-dimensional map
- Cluster data into groups using hierarchical clustering
- Correctly interpret the information contained in the clusters and maps
6.2. Multidimensional scaling ¶
| ID | BOSTON | NY | DC | MIAMI | CHICAGO | SEATTLE | SF | LA | DENVER |
| BOSTON | 0 | 206 | 429 | 1504 | 963 | 2976 | 3095 | 2979 | 1949 |
| NY | 206 | 0 | 233 | 1308 | 802 | 2815 | 2934 | 2786 | 1771 |
| DC | 429 | 233 | 0 | 1075 | 671 | 2684 | 2799 | 2631 | 1616 |
| MIAMI | 1504 | 1308 | 1075 | 0 | 1329 | 3273 | 3053 | 2687 | 2037 |
| CHICAGO | 963 | 802 | 671 | 1329 | 0 | 2013 | 2142 | 2054 | 996 |
| SEATTLE | 2976 | 2815 | 2684 | 3273 | 2013 | 0 | 808 | 1131 | 1307 |
| SF | 3095 | 2934 | 2799 | 3053 | 2142 | 808 | 0 | 379 | 1235 |
| LA | 2979 | 2786 | 2631 | 2687 | 2054 | 1131 | 379 | 0 | 1059 |
| DENVER | 1949 | 1771 | 1616 | 2037 | 996 | 1307 | 1235 | 1059 | 0 |
METRIC MULTIDIMENSIONAL SCALING
--------------------------------------------------------------------------------
Starting config: GOWER'S PRINCIPAL COORDINATES
Type of Data: Dissimilarities
Input dataset: CITIES (D:\Users\Hyo\Cs-Ds\CS\Classes\2014-fall\NewMediaStudies-grad\Borgatti_Data\Ch06\CITIES)
9 items
Initial Stress = 0.019696305
Final Stress = 0.014 after 11 iterations.
Metric MDS coordinates (stress = 0.014)
1 2
------ ------
1 BOSTON 0.410 -0.144
2 NY 0.367 -0.095
3 DC 0.331 -0.031
4 MIAMI 0.374 0.304
5 CHICAGO 0.132 -0.039
6 SEATTLE -0.486 -0.191
7 SF -0.520 0.056
8 LA -0.450 0.156
9 DENVER -0.160 0.016
Coordinates saved as dataset MetricMdsCoord
----------------------------------------
Running time: 00:00:01
Output generated: 23 9 14 15:34:48
UCINET 6.511 Copyright (c) 1992-2012 Analytic Technologies
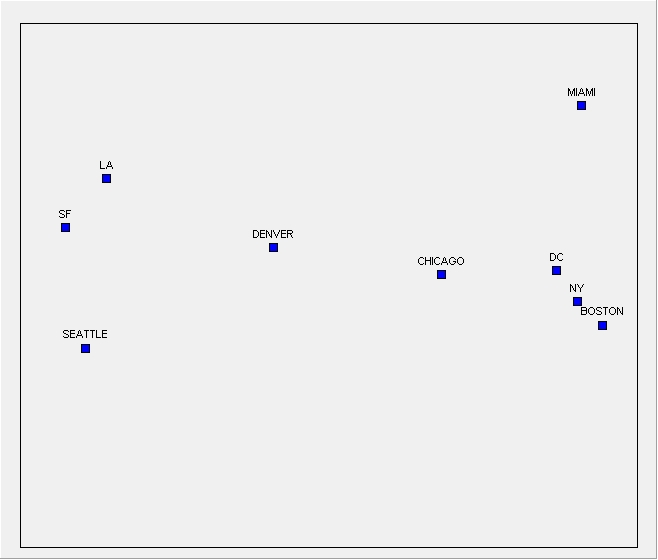
[JPG image (29.54 KB)]
MDS can draw maps in any number of dimensions, but for the purposes of visualizing data on a screen or sheet of paper we use just one or two dimensions.
- distortion = stress (not fitting into the two-dimensional space)
- 0.2 = acceptance level for metric
- 0.12 = for non-metric (ordinal)
- the above case = .014
The first is that the axes are, in themselves, meaningless, and the second is that the orientation of the picture is arbitrary.
. . . two things to look for in interpreting an MDS picture: clusters and dimensions.
6.3. Correspondence analysis ¶
Correspondence analysis refers to a collection of closely related techniques, including optimal scaling and biplot analysis, which are used for a variety of purposes.
. . . primarily as a visualization applied to two-mode data.
. . . primarily as a visualization applied to two-mode data.
6.4. Hierarchical clustering ¶
Given a set of N actors to be clustered, and an N × N distance matrix, the basic process of Johnson’s (1967) hierarchical clustering is this:
- Start by assigning each item to its own cluster, so that if you have N items, you now have N clusters, each containing just one item. Let the distances between the clusters equal the distances between the items they contain.
- Find the closest pair of clusters and merge them into a single cluster, so that now you have one less cluster.
- Compute distances between the new cluster and each of the old clusters.'''
- Repeat steps 2 and 3 until all items are clustered into a single cluster of size N.
Step 3 can be done in different ways, which is what distinguishes
- single-link from
- complete-link (dia-meter, maximum) and
- average-link clustering.
- In single-link clustering (also called the nearest neighbor, the connectedness method and the minimum method), we consider the distance between one cluster and another cluster to be equal to the shortest distance from any member of one cluster to any member of the other cluster.
- In complete-link clustering (also called the diameter or maximum method), we consider the distance between one cluster and another cluster to be equal to the longest distance from any member of one cluster to any member of the other cluster.
- In average-link clustering, we consider the distance between one cluster and another cluster to be equal to the average distance from any member of one cluster to any member of the other cluster. More recently, Newman (2004) has introduced another criterion, which joins the pair of clusters that would maximize Q modularity, a measure of clustering quality.
7. 7 Visualization ¶
Data:  Roethlisberger & Dickson Bank Wiring Room (612 Bytes)
Roethlisberger & Dickson Bank Wiring Room (612 Bytes)
Data: Trade data (1.21 KB)
Trade data (1.21 KB)
Data: Campnet data set (498 Bytes) as in Ch. 2
Campnet data set (498 Bytes) as in Ch. 2
 Roethlisberger & Dickson Bank Wiring Room (612 Bytes)
Roethlisberger & Dickson Bank Wiring Room (612 Bytes)Data:
 Trade data (1.21 KB)
Trade data (1.21 KB)Data:
 Campnet data set (498 Bytes) as in Ch. 2
Campnet data set (498 Bytes) as in Ch. 2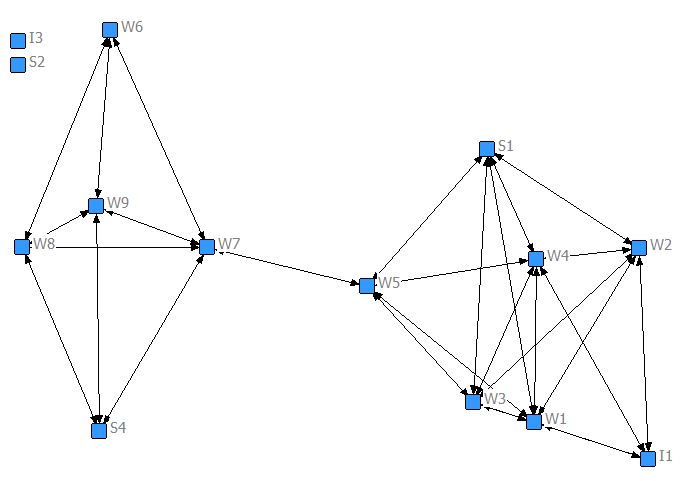
Netdraw output [JPG image (37.95 KB)]
NetDraw Layout -> Attributes at coordinates
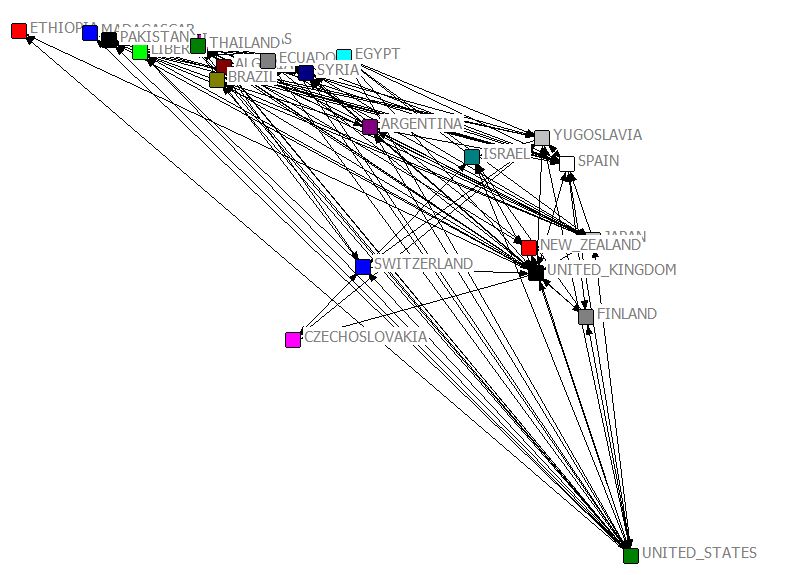
Using coordinates [JPG image (84.34 KB)]
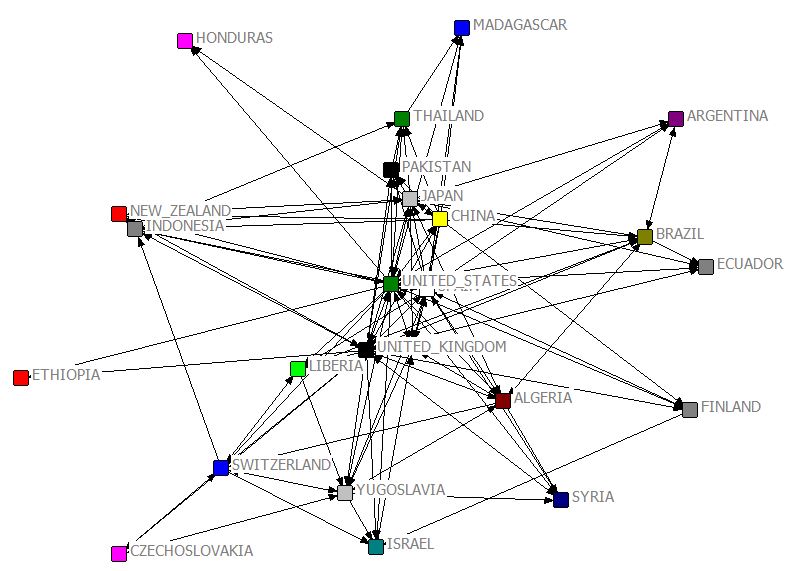
MDS [JPG image (81.82 KB)]
NetDraw Lighting bolt button
8. 8 Testing Hypotheses ¶
Permutation
. . . So you correlate the variables using your sample data, and get a value like 0.384. The classical significance test then tells you the probability of obtaining a correlation that large given that in the population the variables are actually independent (correlation zero). When this probability is really low (less than 0.05), we call it significant and are willing to claim that the variables are actually related in the population, and not just in your sample.
QAP CORRELATION
--------------------------------------------------------------------------------
Data Matrices: PADGB
PADGM
# of Permutations: 5000
Random seed: 1
Method: Fast: no missing values allowed
QAP results for PADGM * PADGB (5000 permutations)
1 2 3 4 5 6 7 8
Obs Value Significa Average Std Dev Minimum Maximum Prop >= O Prop <= O
--------- --------- --------- --------- --------- --------- --------- ---------
Pearson Correlation 0.3719 0.0008 -0.0004 0.0935 -0.1690 0.4395 0.0008 0.9998
QAP Correlations
1 2
PADGB PADGM
----- -----
1 PADGB 1.000 0.372
2 PADGM 0.372 1.000
QAP P-Values
1 2
PADGB PADGM
----- -----
1 PADGB 0.000 0.001
2 PADGM 0.001 0.000
QAP statistics saved as datafile QAP Correlation Results
----------------------------------------
Running time: 00:00:01
Output generated: 07 10 14 15:15:41
UCINET 6.511 Copyright (c) 1992-2012 Analytic Technologies
MULTIPLE REGRESSION QAP VIA DOUBLE DEKKER SEMI-PARTIALLING
--------------------------------------------------------------------------------
# of permutations: 2000
Diagonal valid?: NO
Random seed: 963
Dependent variable: KHTec-ADVICE
Partition variable (if any):
Predicted values: KHTec-ADVICE-mrpred (D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-ADVICE-mrpred
Residual values: KHTec-ADVICE-mrResid (D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-ADVICE-mrResid
Model fit stats: KHTec-ADVICE-mrfit (D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-ADVICE-mrfit
Model coefficients: KHTec-ADVICE-mrcoef (D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-ADVICE-mrcoef
Independent variables: D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-FRIENDSHIP
D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-REPORTS_TO
MODEL FIT
R-Square Adj R-Sqr P-Value Obs Perms
------------ ------------ ------------ ------------ ------------
Model 0.063 0.059 0.000 420 2000
REGRESSION COEFFICIENTS
Un-Stdized Stdized Coef P-value As Large As Small Std Err
------------ ------------ ------------ ------------ ------------ ------------
KHTec-FRIENDSHIP 0.13582 0.11701 0.05097 0.05097 0.94953 0.08288
KHTec-REPORTS_TO 0.47157 0.20177 0.00050 0.00050 1.00000 0.11902
Intercept 0.39694 0.00000 0.00000 0.00000 0.00000 0.00000
-----------------------------------------
Running time: 00:00:01 seconds.
Output generated: 07 10 14 15:13:50
QAP LOGISTIC REGRESSION
--------------------------------------------------------------------------------
Dependent Variable: KHTec-ADVICE (D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-ADVICE
Independent Variables: D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-FRIENDSHIP
D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-REPORTS_TO
# of permutations: 1000
Random seed: 1873119137
Statistics to track: T-Statistics
Data type: Non-Symmetric (directed)
Predicted values: KHTec-ADVICE-pred (D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-ADVICE-pred
Model fit stats: KHTec-ADVICE-fit (D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-ADVICE-fit
Model coefficients: KHTec-ADVICE-coef (D:\Users\Hyo\OneDrive\Ucinet\Ch08\KHTec-ADVICE-coef
Permutation history: history (D:\Users\Hyo\OneDrive\Ucinet\Ch08\history
Dependent variable: : KHTec-ADVICE
Overall fit of the logistic regression model
1 2 3 4 5
LL R-Sqr Sig Obs Perms
--------- --------- --------- --------- ---------
1 Statistics: -274.073 0.065 0.001 420 1000
1 rows, 5 columns, 1 levels.
LR Coefficients & Permutation Results (T-stats used in permutations)
1 2 3 4 5 6 7 8 9 10 11
Coef OddsRat T Sig Avg Min Max SD P(ge) P(le) Perms
--------- --------- --------- --------- --------- --------- --------- --------- --------- --------- ---------
1 Intercept -0.425 0.654 -3.666 1000
2 KHTec-FRIENDSHIP 0.579 1.785 2.418 0.051 0.023 -1.244 0.948 0.345 0.051 0.950 1000
3 KHTec-REPORTS_TO 3.059 21.306 2.956 0.001 -0.010 -1.521 3.059 0.540 0.001 1 1000
3 rows, 11 columns, 1 levels.
-----------------------------------------
Running time: 00:00:01 seconds.
Output generated: 07 10 14 15:21:24
. . . We shall examine the first two time periods to study reciprocity and transitivity. We are interested to know if new friendship ties formed in Week 1 are a result of reciprocity and/or transitivity of ties formed in week 0.
DL N=17 FORMAT = FULLMATRIX DIAGONAL PRESENT LEVEL LABELS: "NEWC0" DATA: 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0
DL N=17 FORMAT = FULLMATRIX DIAGONAL PRESENT LEVEL LABELS: "NEWC1" DATA: 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0
TRANSPOSE
--------------------------------------------------------------------------------
Input dataset: NEWC0D (D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC0D)
Output dataset: NEWC0D-reciprocity (D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC0D-reciprocity)
1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1
- - - - - - - - - - - - - - - - -
1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0
2 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
4 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1
5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
6 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0
7 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0
8 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 1
10 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0
11 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 1 0
12 0 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 1
13 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
15 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0
16 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
17 1 0 1 1 1 0 1 0 1 0 1 1 0 0 0 0 0
Transposed matrix saved as dataset D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC0D-reciprocity
----------------------------------------
Running time: 00:00:01
Output generated: 07 10 14 15:41:16
UCINET 6.511 Copyright (c) 1992-2012 Analytic Technologies
TRANSITIVIZE
--------------------------------------------------------------------------------
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
-- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
1 0 0 0 1 0 1 0 0 1 0 1 1 1 0 1 0 1
2 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 1 1
3 0 0 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1
4 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 1 1
5 0 0 1 1 0 0 0 0 1 0 1 1 0 0 0 0 1
6 1 1 0 1 0 0 1 1 0 1 1 0 1 0 1 0 1
7 0 1 1 1 0 0 0 0 1 0 1 1 0 0 0 0 1
8 1 0 0 1 0 1 1 0 1 1 1 1 1 0 1 0 1
9 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 1
10 1 0 0 1 1 0 1 0 0 0 1 1 1 0 1 0 1
11 0 0 1 1 0 0 0 0 1 0 0 1 0 0 0 0 1
12 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 0 1
13 1 0 0 1 1 1 0 1 0 1 1 0 0 0 1 0 1
14 1 0 0 1 0 0 1 0 1 1 1 1 0 0 1 0 1
15 1 0 0 0 1 0 1 0 1 1 1 1 0 0 0 0 1
16 0 1 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1
17 0 1 1 1 0 0 1 0 1 0 1 1 0 0 0 0 0
17 rows, 17 columns, 1 levels.
-----------------------------------------
Running time: 00:00:01 seconds.
Output generated: 07 10 14 15:41:50
UCINET 6.511 Copyright (c) 1992-2012 Analytic Technologies
QAP LOGISTIC REGRESSION
--------------------------------------------------------------------------------
Dependent Variable: NEWC1D (D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC1D
Independent Variables: D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC0D
D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC0D-reciprocity
D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC0D-transitivity
# of permutations: 10000
Random seed: 2058888892
Statistics to track: T-Statistics
Data type: Non-Symmetric (directed)
Predicted values: NEWC1D-pred (D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC1D-pred
Model fit stats: NEWC1D-fit (D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC1D-fit
Model coefficients: NEWC1D-coef (D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\NEWC1D-coef
Permutation history: history (D:\Users\Hyo\OneDrive\Ucinet\Ch08\NewFrat\history
Dependent variable: : NEWC1D
Overall fit of the logistic regression model
1 2 3 4 5
LL R-Sqr Sig Obs Perms
---------- ---------- ---------- ---------- ----------
1 Statistics: -100.284 0.263 0.000 272 10000
1 rows, 5 columns, 1 levels.
LR Coefficients & Permutation Results (T-stats used in permutations)
1 2 3 4 5 6 7 8 9 10 11
Coef OddsRat T Sig Avg Min Max SD P(ge) P(le) Perms
---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ---------- ----------
1 Intercept -2.764 0.063 -8.096 10000
2 NEWC0D 1.833 6.253 4.053 0.000 -0.007 -2.592 2.672 0.482 0.000 1.000 10000
3 NEWC0D-reciprocity 0.806 2.239 1.943 0.012 -0.013 -1.868 1.160 0.369 0.012 0.988 10000
4 NEWC0D-transitivity 0.923 2.517 1.982 0.045 0.001 -2.359 1.690 0.433 0.045 0.955 10000
4 rows, 11 columns, 1 levels.
-----------------------------------------
Running time: 00:00:03 seconds.
Output generated: 07 10 14 15:43:42
12. 12 Equivalence ¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 RO BO AM BE PE LO VI WI JO GR HU BO MA AL AM BA EL SI -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- ROMULAND 0 7 7 8 11 7 8 5 9 10 7 7 8 7 7 9 8 8 BONAVENTURE 7 0 5 8 12 8 7 8 10 12 9 8 9 8 9 11 10 10 AMBROSE 7 5 0 9 12 9 7 7 10 11 8 8 10 8 9 10 10 10 BERTHOLD 8 8 9 0 10 10 9 10 11 12 11 10 9 10 10 10 10 11 PETER 11 12 12 10 0 10 12 12 13 13 12 12 13 13 11 12 12 13 LOUIS 7 8 9 10 10 0 10 8 10 12 10 9 10 9 7 10 10 10 VICTOR 8 7 7 9 12 10 0 8 11 12 10 9 11 9 10 11 10 9 WINFRID 5 8 7 10 12 8 8 0 8 9 6 5 8 7 8 8 9 9 JOHN 9 10 10 11 13 10 11 8 0 10 10 10 11 10 9 11 11 11 GREGORY 10 12 11 12 13 12 12 9 10 0 9 9 11 10 11 9 12 12 HUGH 7 9 8 11 12 10 10 6 10 9 0 5 9 7 9 9 10 9 BONIFACE 7 8 8 10 12 9 9 5 10 9 5 0 7 5 9 9 9 9 MARK 8 9 10 9 13 10 11 8 11 11 9 7 0 6 9 9 9 9 ALBERT 7 8 8 10 13 9 9 7 10 10 7 5 6 0 9 9 9 9 AMAND 7 9 9 10 11 7 10 8 9 11 9 9 9 9 0 9 9 9 BASIL 9 11 10 10 12 10 11 8 11 9 9 9 9 9 9 0 7 9 ELIAS 8 10 10 10 12 10 10 9 11 12 10 9 9 9 9 7 0 5 SIMPLICIUS 8 10 10 11 13 10 9 9 11 12 9 9 9 9 9 9 5 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 RO BO AM BE PE LO VI WI JO GR HU BO MA AL AM BA EL SI -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- ROMULAND 0 7 7 8 11 7 8 5 9 10 7 7 8 7 7 9 8 8 BONAVENTURE 7 0 5 8 12 8 7 8 10 12 9 8 9 8 9 11 10 10 AMBROSE 7 5 0 9 12 9 7 7 10 11 8 8 10 8 9 10 10 10 BERTHOLD 8 8 9 0 10 10 9 10 11 12 11 10 9 10 10 10 10 11 PETER 11 12 12 10 0 10 12 12 13 13 12 12 13 13 11 12 12 13 LOUIS 7 8 9 10 10 0 10 8 10 12 10 9 10 9 7 10 10 10 VICTOR 8 7 7 9 12 10 0 8 11 12 10 9 11 9 10 11 10 9 WINFRID 5 8 7 10 12 8 8 0 8 9 6 5 8 7 8 8 9 9 JOHN 9 10 10 11 13 10 11 8 0 10 10 10 11 10 9 11 11 11 GREGORY 10 12 11 12 13 12 12 9 10 0 9 9 11 10 11 9 12 12 HUGH 7 9 8 11 12 10 10 6 10 9 0 5 9 7 9 9 10 9 BONIFACE 7 8 8 10 12 9 9 5 10 9 5 0 7 5 9 9 9 9 MARK 8 9 10 9 13 10 11 8 11 11 9 7 0 6 9 9 9 9 ALBERT 7 8 8 10 13 9 9 7 10 10 7 5 6 0 9 9 9 9 AMAND 7 9 9 10 11 7 10 8 9 11 9 9 9 9 0 9 9 9 BASIL 9 11 10 10 12 10 11 8 11 9 9 9 9 9 9 0 7 9 ELIAS 8 10 10 10 12 10 10 9 11 12 10 9 9 9 9 7 0 5 SIMPLICIUS 8 10 10 11 13 10 9 9 11 12 9 9 9 9 9 9 5 0
13.1. 7. Equivalence ¶
Use the Davis data
Use the two output files, with the original data file
Tools -> Similarities & Distances---
input: davis output: davis-Mat-C Matches . . . . Cols---
input: davis output: davis-Mat-R Matches . . . . Rows---
Use the two output files, with the original data file
Network -> Cohesion -> Density with Group input: davis row partition: davis-Mat-R columns partion: davis-Mat-C







![[http]](/imgs/http.png)