FrontPage › Correlation
Difference between r1.1 and the current
@@ -4,7 +4,7 @@
== r ==||||||||<table class='wikiLeft'> 상관관계 데이터 ||
||사람||X||Y||<|8> [[Attachment(r_eg.01.png,align=left,caption="Figure 1.",selflink)]] ||
||사람||X||Y||<|8> [[Attachment(r_eg.01.png,align=left,caption='Figure 1.',selflink)]] ||
||A||1||1||||B||1||3||
||C||3||2||
@@ -34,9 +34,14 @@
[[HTML(<div style="clear:both"></div>)]]=== 상관관계가 사용될 때 ===
1. prediction 예측
* 대학생활 만족도와 졸업 10년 후 행복지수에 대한 데이터를 지속적으로 모아서 관측, 분석을 하게 되면;
* 만족도만을 아는 상태에서 . . .
1. Validity 측정
* Validity test: Comparing r to other verified methods in order to confirm (check) __my method is valid__.
* 내가 고안한 IQ 테스트 방법은 비록 원 IQ 테스트 방법과 다르지만, 결과 값은 서로 상관관계가 높다.
1. Theory backup
1. Reliablity 측정
* Half-and-half reliability test.
== Pearson's r ==
Pearson's r:: 두 변인 간의 선형적 관계의 크기와 방향성을 측정하는 방법
@@ -44,22 +49,27 @@
\begin{eqnarray}r & = & \frac{\text{degree to which X and Y vary together}}{\text{degree to which X and Y vary separately}} \nonumber \\
& = & \frac{\text{covariablity of X and Y}}{\text{variability of X and Y separately}} \nonumber \\
& = & \frac{Cov[X,Y]}{Var[X]Var[Y]} \\
& = & \frac{Cov[X,Y]}{\sqrt{Var[X]Var[Y]}} \\
& = & \frac{SP_{XY}}{\sqrt{SS_X SS_Y}} \end{eqnarray}
}}}
위에서 (1), (2)는 동일하다. 왜냐하면 . . . . Cov[X,Y]와 Var[X], Var[Y}에 공히 들어가는 분모는 n-1 (degrees of freedom)이기 때문이다.
위에서 (1), (2)는 동일하다. 왜냐하면 . . . . $Cov[X,Y]$ 와 Var[X], Var[Y}에 공히 들어가는 분모는 n-1 (degrees of freedom)이기 때문이다.
이를 그림으로 나타내 보면 아래와 같다.
http://vassarstats.net/textbook/circles.gif
위에서 각각의 동그라미는 X 변인과 Y 변인의 variability, 즉 variance를 의미한다고 하면, 위의 그림은 X와 Y가 변하는 정도가 동그라미 정도의 크기를 가지며, 각각의 요소들이 서로 따로따로 논다는 것을 알 수 있다. 즉, Co-vary하지 않다는 것을 알 수 있다. 반면, 아래의 예는 X와 Y의 변하는 정도가 나타나면서 동시에, 각 변인이 서로 동시에 변하는 정도가 어느정도인지 가늠을 할 수 있게 해 준다. Y 입장에서 보면 Y가 변하는 정도 붉은 동그라미 크기 중에서 X와 겹치는 정도를 제외한 정도는 X와 함께 변하는 것이 아닌, Y 고유의 변화정도이다. 이를 residual variance라고 하고, 겹치는 정도는 regression variance라고 이야기 하는데, 이에 대해서는 다음에 설명하도록 한다. 또한 X와 겹치는 변량(X와 Y가 동시에 변화하는 것을 고려한 변량 = $Cov[X, Y]$ )과 Y 전체 변량(분산)의 비율을 $r^2$ 이라고 하는데 이는 r 값을 제곱하여 구한다. 반대로, X와 겹치지 않는 변량과 전체 변량의 비율은 ( $1 - r^2$ )으로 표현한다.
=== Sum of Products of Deviations ==={{{#!latex
\begin{eqnarray}
SP & = & \displaystyle \sum (X-\overline{X})(Y-\overline{Y}) \nonumber \\
& = & \displaystyle \sum XY - \frac{\sum X \small \sum Y}{n} \nonumber
& = & \displaystyle \sum XY - \displaystyle \frac{\sum X \small \sum Y}{n} \nonumber
\end{eqnarray}}}}
Deviation score = $(X-\overline{X})$ 이라고 할 때, 우리가 관심이 있는 것은 어떤 한 케이스의 X가 변화할 때, 해당 케이스의 y값이 어떻게 (동시에) 변화하는가이므로, 이 상황에 맞는 deviation score는 $(X-\overline{X})(Y-\overline{Y})$ 라고 할 수 있다. 이에 degress of freedom에 해당하는 $n-1$ 로 나누어 준 값을 X,Y에 대한 Covariance라고 하며, $Cov[X,Y]$ 라고 표기한다.
Deviation score = $(X-\overline{X})$ 이라고 할 때, 우리가 관심이 있는 것은 어떤 한 케이스의 X가 변화할 때, 해당 케이스의 y값이 어떻게 (동시에) 변화하는가이므로, 이 상황에 맞는 deviation score는 $(X-\overline{X})(Y-\overline{Y})$ 라고 할 수 있다. 이에 degress of freedom에 해당하는 $n-1$ 로 나누어 준 값을 X,Y에 대한 Covariance라고 하며, $Cov[X,Y]$ 라고 표기한다. 즉, $ COV_{xy} = \frac{SP}{n}$
참고:
{{{#!latex
@@ -82,6 +92,10 @@
|| 5 || 7 || +2 || +2 || +4 |||| || || || || [[HTML( )]]+6 = $SP$ ||
X 평균 = 3
Y 평균 = 5
[[HTML(<div class='clear'></div>)]]
{{{#!latex
@@ -220,7 +234,7 @@
연수입, 교육량, 나이, 그리고 지능 간의 관계를 분석하였다 (n=30). 변인들 간의 상관관계를 정리한 결과를 요약한 표1에 나타냈었다. 통계적으로 유의미한 상관관계는 표에 정리되었다.
||||||||<table class='wikiLeft'> TABLE 1. ||
||||||||<table class='wikiCenter'> TABLE 1. ||
||||||||Correlation matrix for income, amount of education, age, and IQ |||| || Education || Age || IQ ||
||Income || +.65^**^ || +.41^**^ || +.27 ||
@@ -260,13 +274,13 @@
=== Spearman's rho 값 구하기 ===||||<table class='wikiLeft'> 원 데이터 || |||||| '''순위''' ||
|| X || Y ||<|6> || X || Y || XY ||
|| 3 || 12 || 1 || 5 || 5 ||
|| 4 || 5 || 2 || 3 || 6 ||
|| 5 || 6 || 3 || 4 || 12 ||
|| 10 || 4 || 4 || 2 || 8 ||
|| 13 || 3 || 5 || 1 || 5 ||
|| || || || || || $36 = \Sigma XY$ ||
|| X || Y || || X || Y || XY ||
|| 3 || 12 || || 1 || 5 || 5 ||
|| 4 || 5 || || 2 || 3 || 6 ||
|| 5 || 6 || || 3 || 4 || 12 ||
|| 10 || 4 || || 4 || 2 || 8 ||
|| 13 || 3 || || 5 || 1 || 5 ||
||||||| || || || $36 = \Sigma XY$ ||
[[HTML(<div class='clear'></div>)]]{{{#!latex
\begin{eqnarray}
1. r ¶
| 상관관계 데이터 | |||
| 사람 | X | Y | 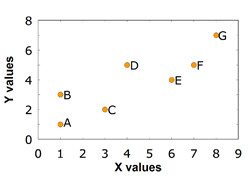 Figure 1. [PNG image (8.73 KB)] |
| A | 1 | 1 | |
| B | 1 | 3 | |
| C | 3 | 2 | |
| D | 4 | 5 | |
| E | 6 | 4 | |
| F | 7 | 5 | |
| G | 8 | 7 | |
상관관계이란 (correlation) 두 변인 간의 관계를 측정하고 묘사하기 위한 통계학적 기법을 뜻한다. 상관관계 측정은 실험보다는 현상에 대한 관찰 기록에 많이 사용된다. 가령 11살 아동의 키와 몸무게의 관계에 관심을 갖는다는 것은, 키라는 변인과 몸무게라는 변인[1] 간의 관계를 알아보려 하는 것이다. 흔히 두 변인은 X 와 Y 로 사용되며, 아래의 그림처럼, 표와 그래프가 데이터 표현에 이용된다.
1.1. 상관관계의 특징 ¶
상관관계는 아래 세 가지 특징을 갖는다.
관계의 방향성 ::
관계의 방향성에 대해서 알려준다. + 사인의 경우, 선형적인 관계가 양의 관계임을, - 사인인 경우에는 음의 관계를 나타내준다고 해석한다.
관계의 방향성에 대해서 알려준다. + 사인의 경우, 선형적인 관계가 양의 관계임을, - 사인인 경우에는 음의 관계를 나타내준다고 해석한다.
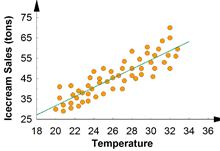 Figure 1-1. [PNG image (15.95 KB)] | 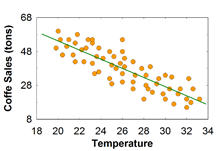 Figure 1-2. [PNG image (15.75 KB)] |
- 관계의 형태 (form)
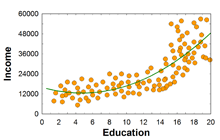 Figure 2-1. [PNG image (17.08 KB)]
Figure 2-1. [PNG image (17.08 KB)]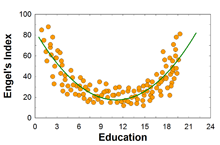 Figure 2-2. [PNG image (17.21 KB)]
Figure 2-2. [PNG image (17.21 KB)]
- 관계의 정도 (힘)
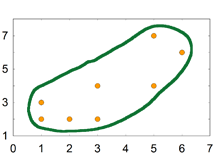 Figure_4-1. [PNG image (9.11 KB)]
Figure_4-1. [PNG image (9.11 KB)]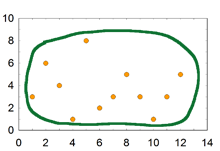 Figure 4-2. [PNG image (9.6 KB)]
Figure 4-2. [PNG image (9.6 KB)]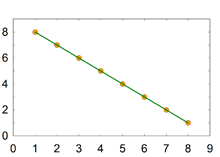 Figure_4-3. [PNG image (6.49 KB)]
Figure_4-3. [PNG image (6.49 KB)]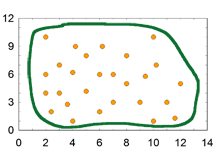 Figure 4-4. [PNG image (11.4 KB)]
Figure 4-4. [PNG image (11.4 KB)]
1.2. 상관관계가 사용될 때 ¶
- prediction 예측
- 대학생활 만족도와 졸업 10년 후 행복지수에 대한 데이터를 지속적으로 모아서 관측, 분석을 하게 되면;
- 만족도만을 아는 상태에서 . . .
- 대학생활 만족도와 졸업 10년 후 행복지수에 대한 데이터를 지속적으로 모아서 관측, 분석을 하게 되면;
- Validity 측정
- Validity test: Comparing r to other verified methods in order to confirm (check) my method is valid.
- 내가 고안한 IQ 테스트 방법은 비록 원 IQ 테스트 방법과 다르지만, 결과 값은 서로 상관관계가 높다.
- Validity test: Comparing r to other verified methods in order to confirm (check) my method is valid.
- Theory backup
- Reliablity 측정
- Half-and-half reliability test.
- Half-and-half reliability test.
2. Pearson's r ¶
- Pearson's r
- 두 변인 간의 선형적 관계의 크기와 방향성을 측정하는 방법
![\begin{eqnarray}
r & = & \frac{\text{degree to which X and Y vary together}}{\text{degree to which X and Y vary separately}} \nonumber \\
& = & \frac{\text{covariablity of X and Y}}{\text{variability of X and Y separately}} \nonumber \\
& = & \frac{Cov[X,Y]}{\sqrt{Var[X]Var[Y]}} \\
& = & \frac{SP_{XY}}{\sqrt{SS_X SS_Y}}
\end{eqnarray}
\begin{eqnarray}
r & = & \frac{\text{degree to which X and Y vary together}}{\text{degree to which X and Y vary separately}} \nonumber \\
& = & \frac{\text{covariablity of X and Y}}{\text{variability of X and Y separately}} \nonumber \\
& = & \frac{Cov[X,Y]}{\sqrt{Var[X]Var[Y]}} \\
& = & \frac{SP_{XY}}{\sqrt{SS_X SS_Y}}
\end{eqnarray}](/_cache/latex/7/7a/13466a2114d692828c131b25da9a59ca.png)
![$Cov[X,Y]$ $Cov[X,Y]$](/_cache/latex/7/79/e792fd9accabbb483207d5e9cca560cb.png) 와 VarX, Var[Y}에 공히 들어가는 분모는 n-1 (degrees of freedom)이기 때문이다.
와 VarX, Var[Y}에 공히 들어가는 분모는 n-1 (degrees of freedom)이기 때문이다. 이를 그림으로 나타내 보면 아래와 같다.
위에서 각각의 동그라미는 X 변인과 Y 변인의 variability, 즉 variance를 의미한다고 하면, 위의 그림은 X와 Y가 변하는 정도가 동그라미 정도의 크기를 가지며, 각각의 요소들이 서로 따로따로 논다는 것을 알 수 있다. 즉, Co-vary하지 않다는 것을 알 수 있다. 반면, 아래의 예는 X와 Y의 변하는 정도가 나타나면서 동시에, 각 변인이 서로 동시에 변하는 정도가 어느정도인지 가늠을 할 수 있게 해 준다. Y 입장에서 보면 Y가 변하는 정도 붉은 동그라미 크기 중에서 X와 겹치는 정도를 제외한 정도는 X와 함께 변하는 것이 아닌, Y 고유의 변화정도이다. 이를 residual variance라고 하고, 겹치는 정도는 regression variance라고 이야기 하는데, 이에 대해서는 다음에 설명하도록 한다. 또한 X와 겹치는 변량(X와 Y가 동시에 변화하는 것을 고려한 변량 = ![$Cov[X, Y]$ $Cov[X, Y]$](/_cache/latex/e/ea/8974cb3dfab394182ab3eca5ed2a304b.png) )과 Y 전체 변량(분산)의 비율을
)과 Y 전체 변량(분산)의 비율을 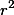 이라고 하는데 이는 r 값을 제곱하여 구한다. 반대로, X와 겹치지 않는 변량과 전체 변량의 비율은 (
이라고 하는데 이는 r 값을 제곱하여 구한다. 반대로, X와 겹치지 않는 변량과 전체 변량의 비율은 (  )으로 표현한다.
)으로 표현한다.
![$Cov[X, Y]$ $Cov[X, Y]$](/_cache/latex/e/ea/8974cb3dfab394182ab3eca5ed2a304b.png) )과 Y 전체 변량(분산)의 비율을
)과 Y 전체 변량(분산)의 비율을 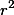 이라고 하는데 이는 r 값을 제곱하여 구한다. 반대로, X와 겹치지 않는 변량과 전체 변량의 비율은 (
이라고 하는데 이는 r 값을 제곱하여 구한다. 반대로, X와 겹치지 않는 변량과 전체 변량의 비율은 (  )으로 표현한다.
)으로 표현한다. 2.1. Sum of Products of Deviations ¶
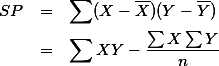
 이라고 할 때, 우리가 관심이 있는 것은 어떤 한 케이스의 X가 변화할 때, 해당 케이스의 y값이 어떻게 (동시에) 변화하는가이므로, 이 상황에 맞는 deviation score는
이라고 할 때, 우리가 관심이 있는 것은 어떤 한 케이스의 X가 변화할 때, 해당 케이스의 y값이 어떻게 (동시에) 변화하는가이므로, 이 상황에 맞는 deviation score는 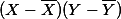 라고 할 수 있다. 이에 degress of freedom에 해당하는
라고 할 수 있다. 이에 degress of freedom에 해당하는  로 나누어 준 값을 X,Y에 대한 Covariance라고 하며,
로 나누어 준 값을 X,Y에 대한 Covariance라고 하며, ![$Cov[X,Y]$ $Cov[X,Y]$](/_cache/latex/7/79/e792fd9accabbb483207d5e9cca560cb.png) 라고 표기한다. 즉,
라고 표기한다. 즉, 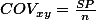
참고:
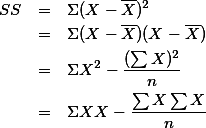
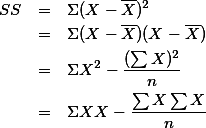
2.2. e.g. 1, ¶
| Example | ||||
| Scores | Deviation score | Products | ||
| X | Y |  |  | 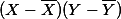 |
| 1 | 3 | -2 | -2 | +4 |
| 2 | 6 | -1 | +1 | -1 |
| 4 | 4 | +1 | -1 | -1 |
| 5 | 7 | +2 | +2 | +4 |
+6 = 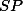 | ||||
X 평균 = 3
Y 평균 = 5
이 예는  의 공식을 사용하여 구한 예이다. 반면에,
의 공식을 사용하여 구한 예이다. 반면에, 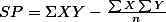 의 공식을 사용하면,
의 공식을 사용하면,
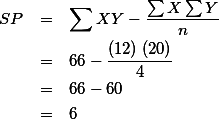 으로 똑같은 결과를 갖는다. 위는 Sum of Products (SP) 의 값을 구한 것이고
으로 똑같은 결과를 갖는다. 위는 Sum of Products (SP) 의 값을 구한 것이고 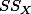 와
와 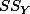 값을 구해 보면:
값을 구해 보면:
 의 공식을 사용하여 구한 예이다. 반면에,
의 공식을 사용하여 구한 예이다. 반면에, 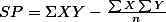 의 공식을 사용하면,
의 공식을 사용하면,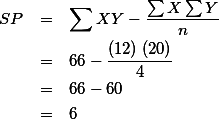 으로 똑같은 결과를 갖는다. 위는 Sum of Products (SP) 의 값을 구한 것이고
으로 똑같은 결과를 갖는다. 위는 Sum of Products (SP) 의 값을 구한 것이고 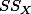 와
와 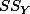 값을 구해 보면:
값을 구해 보면:
| Example | ||||
| X | Y | XY | X2 | Y2 |
| 1 | 3 | 3 | 1 | 9 |
| 2 | 6 | 12 | 4 | 36 |
| 4 | 4 | 16 | 16 | 16 |
| 5 | 7 | 35 | 25 | 49 |
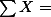 12 12 | 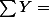 20 20 | 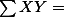 66 66 | 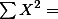 46 46 | 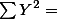 110 110 |
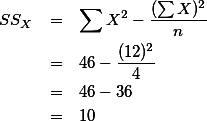
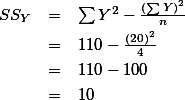
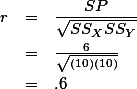
2.3. e.g. 2, ¶
테이블의 데이터에 대한 scatterplot을 그려 보면 그림과 같다.
| Example 2 | ||
| X | Y | 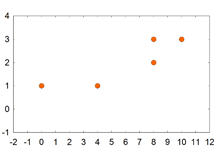 Figure 5. [PNG image (4.45 KB)] |
| 0 | 1 | |
| 10 | 3 | |
| 4 | 1 | |
| 8 | 2 | |
| 8 | 3 | |
| Example 2 | ||||||||
| Scores | Deviation score | Deviation score2 | Products | |||||
| X | Y | X2 | Y2 |  |  | 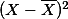 | 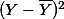 | 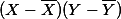 |
| 0 | 1 | 0 | 1 | -6 | -1 | 36 | 1 | 6 |
| 10 | 3 | 100 | 9 | 4 | 1 | 16 | 1 | 4 |
| 4 | 1 | 16 | 2 | -2 | -1 | 4 | 1 | 2 |
| 8 | 2 | 64 | 4 | 2 | 0 | 4 | 0 | 0 |
| 8 | 3 | 64 | 9 | 2 | 1 | 4 | 1 | 2 |
| t = 30 | 10 | 234 | 24 | SSX = 64 | SSY = 4 | SP = 14 | ||
 = 6 = 6 | 2 | |||||||
위에서 구한 SSX, SSY, 그리고 SP 값을 대입해 보면,
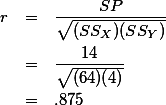
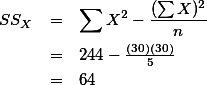
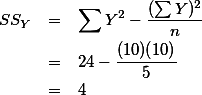
2.4. Pearson's r 의 의미 ¶
Relations, not cause-effect
Interpretation with limited range
Outliers
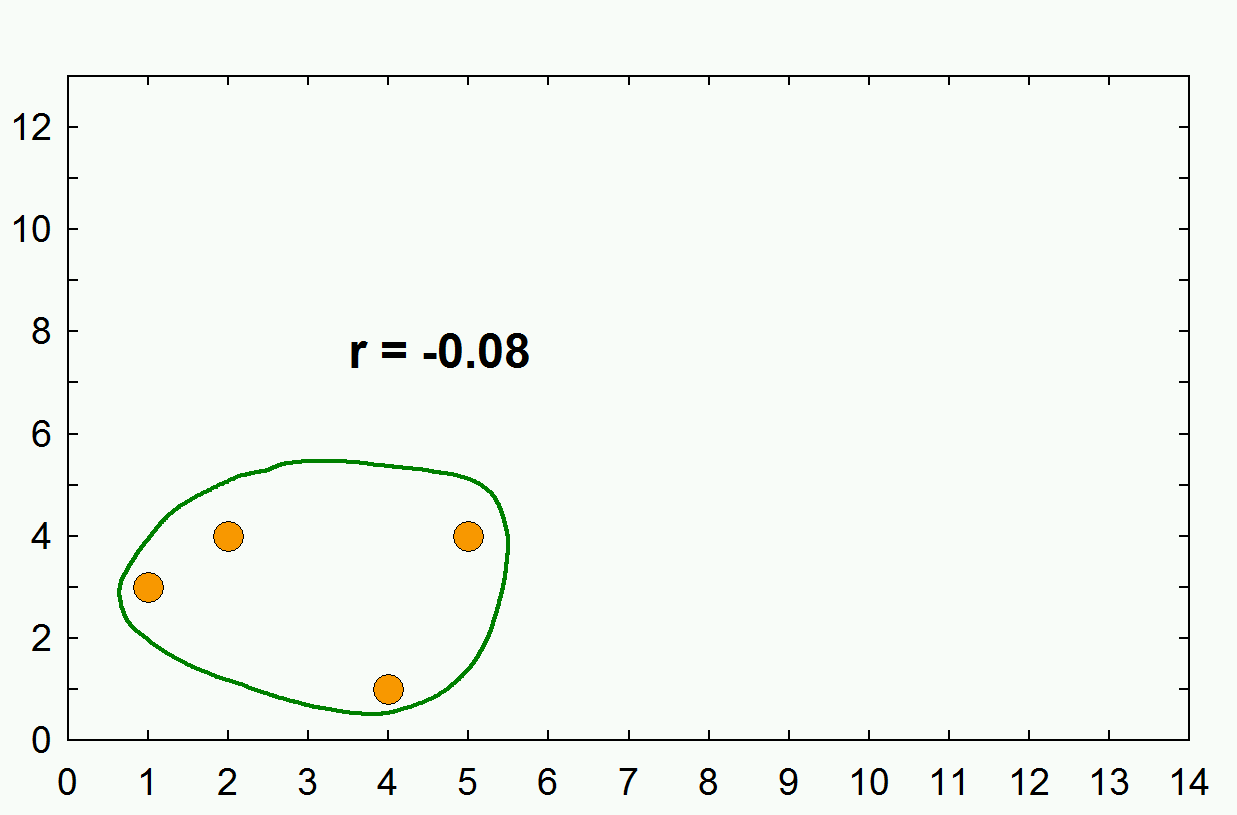
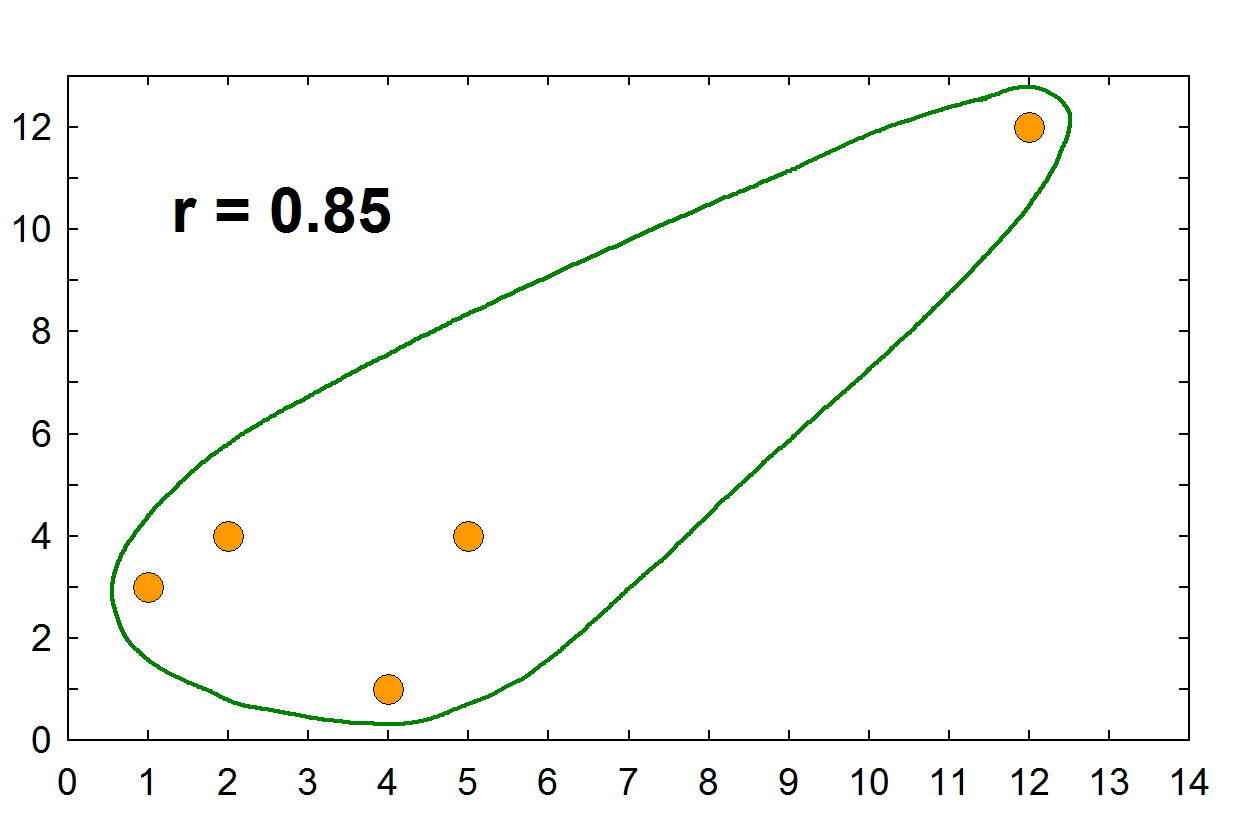
Interpretation of r value
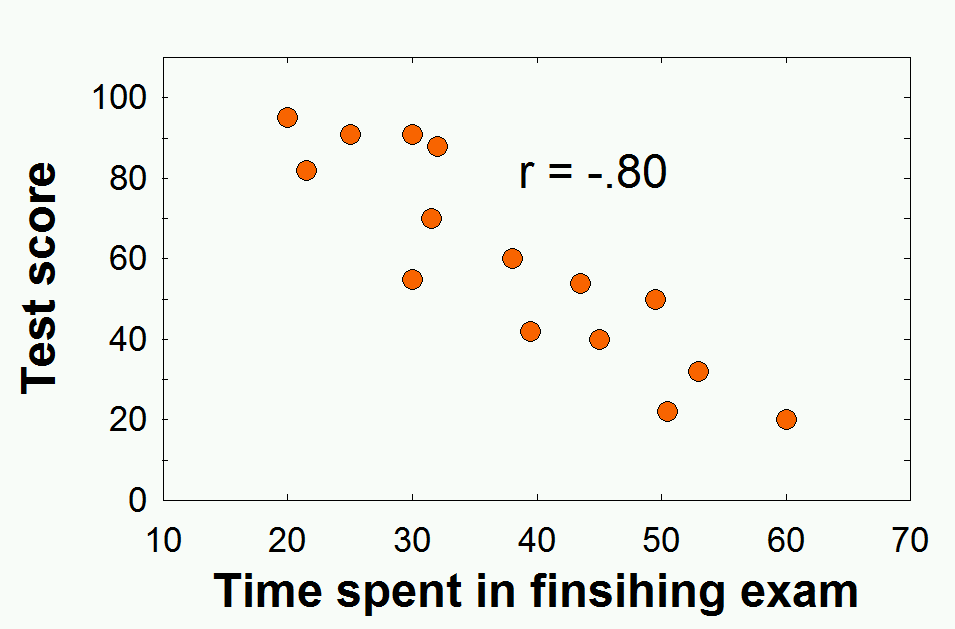
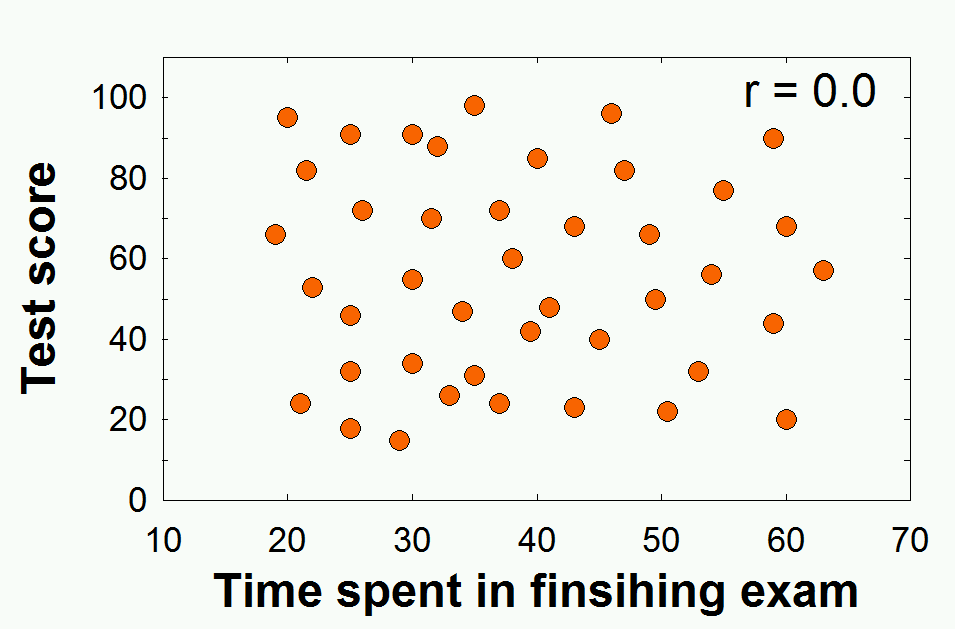
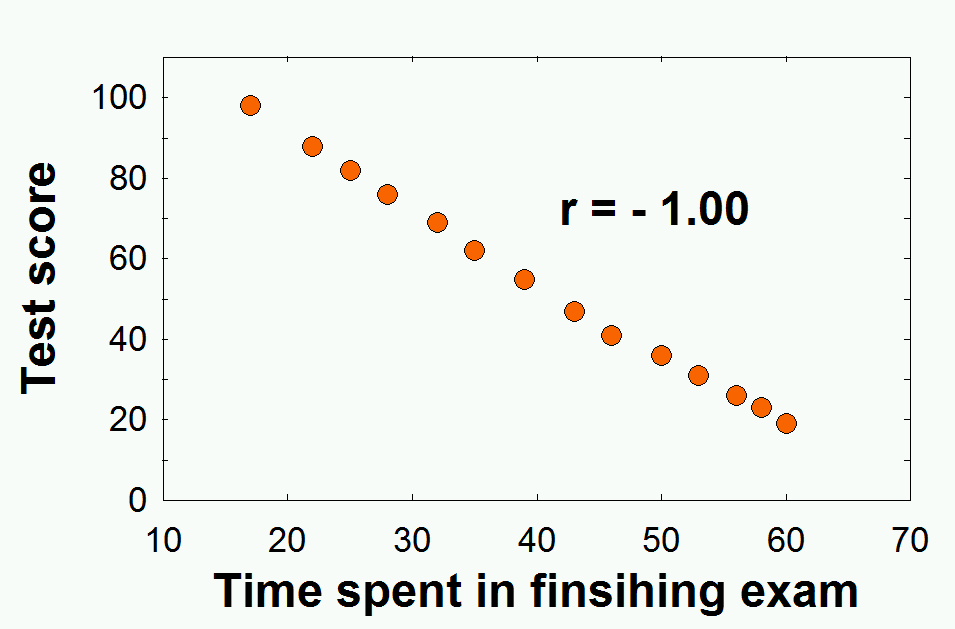

Figure 6. Correlation And Causation [PNG image (19.69 KB)]
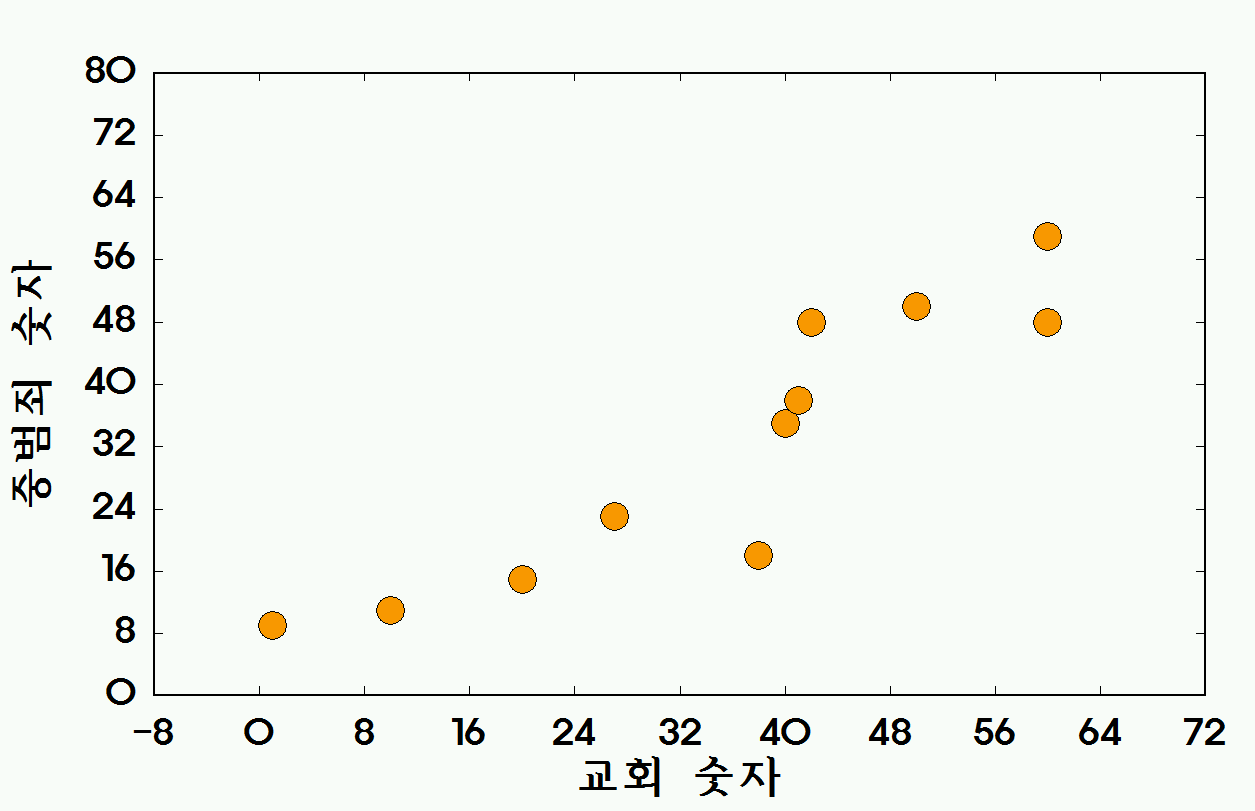
상관관계 계수는 단순히 두 변인 (x, y) 간의 관계가 있다는 것을 알려줄 뿐, 왜 그 관계가 있는지는 설명하지 않는다. 바꿔 말하면, 충분한 r 값을 구했다고 해서 이 값이 두 변인 간의 원인과 결과의 관계를 말한다고 이야기 하면 안된다. 예를 들면 아이스크림의 판매량과 성범죄가 서로 상관관계에 있다고 해서, 전자가 후자의 원인이라고 단정할 수 있는 근거는 없다. 이는 연구자의 논리적인 판단 혹은 이론적인 판단에 따른다.
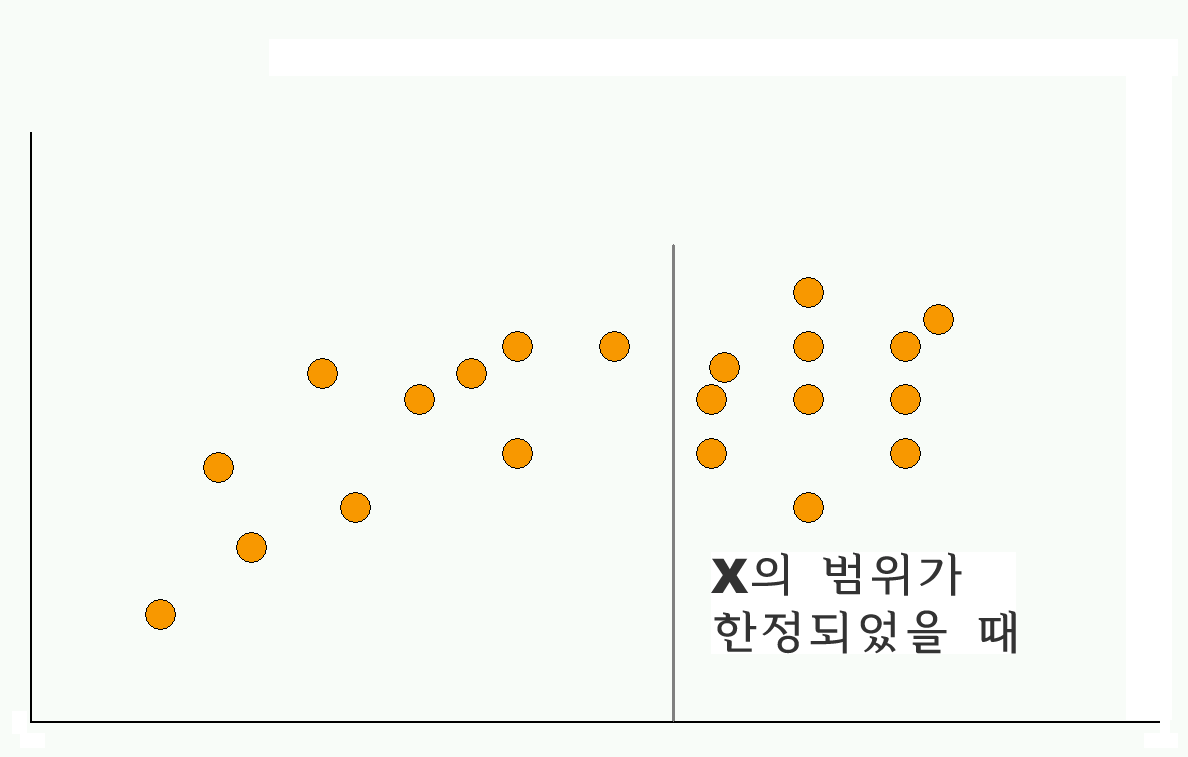
Interpretation with limited range

Figure_7._Correlation_And_Range [PNG image (26.84 KB)]

Figure_7._Correlation_And_Range [PNG image (31.23 KB)]
데이터의 Range에 대한 판단에 신중해야 한다. 왜냐 하면, 데이터의 어느 곳을 자르느냐에 따라서 r 값이 심하게 변하기 때문이다.
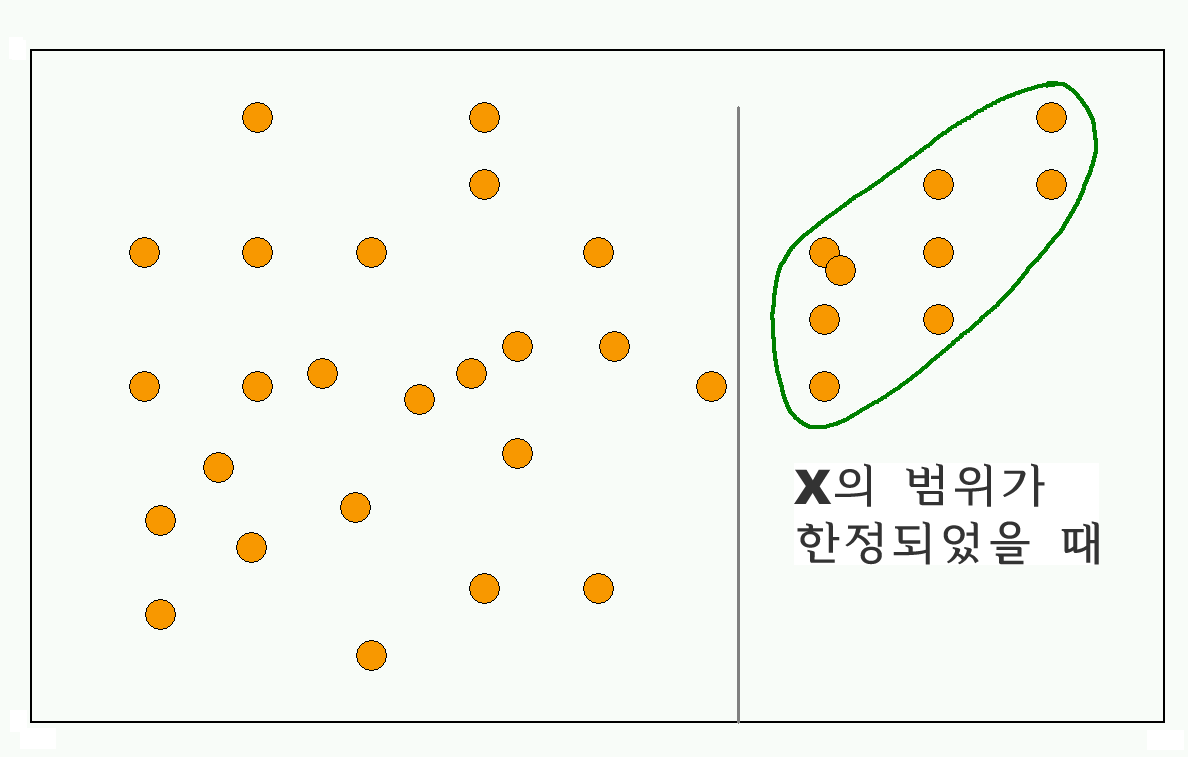
Outliers

Figure_7._Correlation_And_Extreme_Data [PNG image (28.83 KB)]

Figure_7._Correlation_And_Extreme_Data [PNG image (32.24 KB)]
위의 설명과 관련하여, 만약에 아주 심한 Outlier가 존재한다면 두 변인 간의 상관관계에 심한 영향을 준다.
Interpretation of r value

Figure_8._Correlation_And_Strength [PNG image (16.75 KB)]

Figure_8._Correlation_And_Strength [PNG image (18.37 KB)]

Figure_8._Correlation_And_Strength [PNG image (16.55 KB)]
r 값으로 얻는 단위는 상관관계의 정도를 정확히 말해 주지 않는다. 예를 들면 r = +.5 은 0 - 1 까지의 반이므로 적당한 량의 상관관계를 보여주고 있다고 생각할 수 있으나, 이는 사실이 아니다. 정확한 양을 이야기 하려면, r 값에 제곱을 해준 값을 이야기 해야 한다. 따라서, r = +.5 인경우 .5^2 값인 .25 즉, 25%가 두 변인 간의 상관관계의 양이다.
2.5. Pearson's r을 이용한 가설 검증 ¶
기본적으로 두 변인 (보통 한 subject 혹은 participant의 두 변인 기록으로 이루어진 데이터) 간에 상관관계가 있는가에 대한 질문이 연구문제 혹은 가설로 만들어지며, 만약에 이 관계가 없다면, 이라는 질문의 영가설을 통해서 이를 검증한다. 즉,
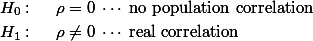
2.7. 학술논문 보고 ¶
데이터의 상관관계를 살펴본 결과 개인의 교육양과 (년도수) 연수입 (원) 간에는 통계학적으로 유의미한 상관관계가 있다고 판단되었다 (r = +.65, n = 30, p < .01).
연수입, 교육량, 나이, 그리고 지능 간의 관계를 분석하였다 (n=30). 변인들 간의 상관관계를 정리한 결과를 요약한 표1에 나타냈었다. 통계적으로 유의미한 상관관계는 표에 정리되었다.
| TABLE 1. | |||
| Correlation matrix for income, amount of education, age, and IQ | |||
| Education | Age | IQ | |
| Income | +.65** | +.41** | +.27 |
| Education | +.11 | +.38* | |
| Age | -.02 | ||
| n=30 * p < .05, two tails ** p < .01, twotails | |||
2.8. exercise ¶
- 연구자가 얻은 r = -.41 (n=25) 일때, 이 샘플이 모집단에서 나타나는 두 변인간의 상관관계가 통계적으로 유의미하다고 할 수 있는가?
- n=20 일때, r값은 어떤 값을 가져야 모집단의 두 변인 간의 상관관계가 의미가 있다고 하겠는가?
- 샘플사이즈가 작아질 수 록, 유의미한 상관관계를 갖기 위한 r값은 어떻게 되야 하는가? 왜 그런가?
3. Spearman Correlation ¶
| Scores | ||
| Person | X | Y |
| A | 4 | 9 |
| B | 2 | 2 |
| C | 10 | 10 |
| D | 3 | 8 |
| Scores | ||
| Person | X | Y |
| A | 3 | 3 |
| B | 1 | 1 |
| C | 4 | 4 |
| D | 2 | 2 |
Figure_4-1. [PNG image (12.47 KB)]
Figure_4-2. [PNG image (17.56 KB)]
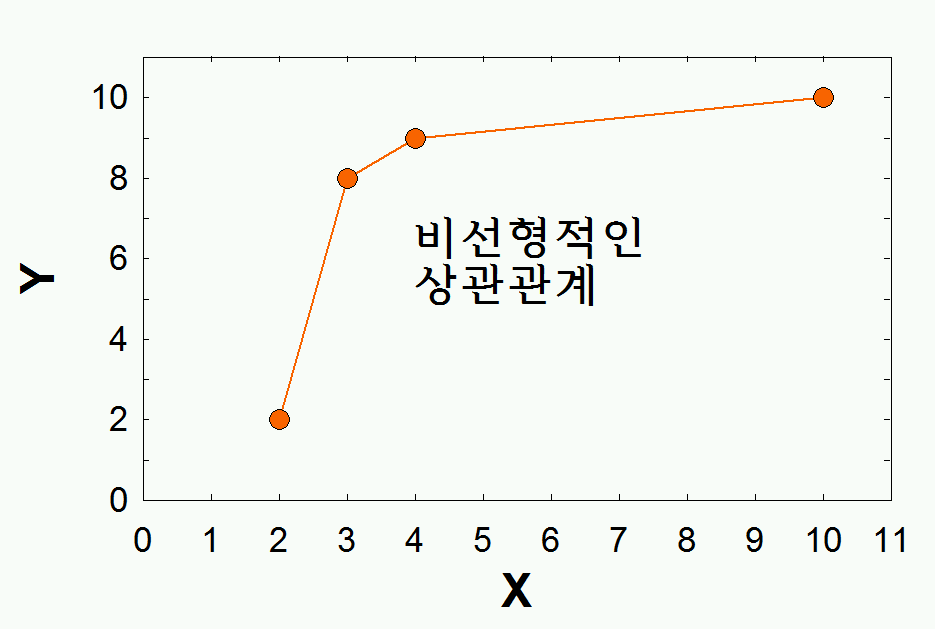
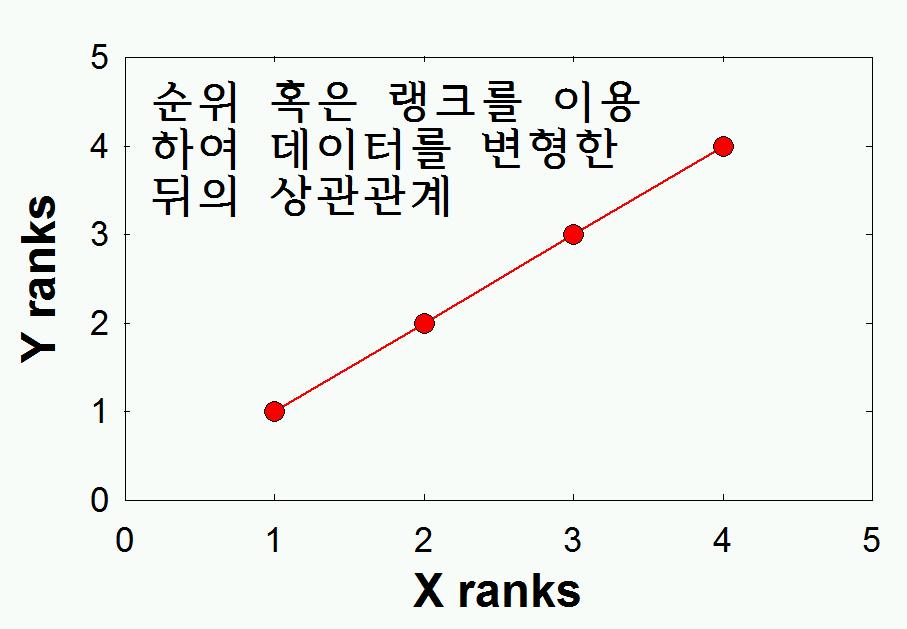
따라서, Spearman rho는
- 순위측정 데이터에 사용 (ordinal measured).
- 상관관계의 지속성에 관심을 둘 때 사용. 즉, 계속 증가하는가, 감소하는 추세인가, 등등에 사용
3.1. Spearman's rho 값 구하기 ¶
| 원 데이터 | 순위 | ||||
| X | Y | X | Y | XY | |
| 3 | 12 | 1 | 5 | 5 | |
| 4 | 5 | 2 | 3 | 6 | |
| 5 | 6 | 3 | 4 | 12 | |
| 10 | 4 | 4 | 2 | 8 | |
| 13 | 3 | 5 | 1 | 5 | |
| | | 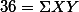 | ||||


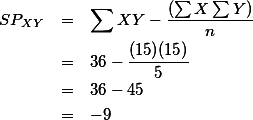
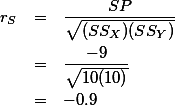
4. Regression ¶
Regression은 이야기할 내용이 많으므로 Regression 참조.



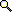




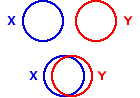
![[http]](/imgs/http.png)
