Difference between r1.47 and the current
@@ -10,10 +10,10 @@
{{|{{{#!latex
\begin{align*}
E[aX] = & a E[X] \\
E[X+Y] = & E[X] + E[Y] \\
Var[aX] = & a^{\tiny{2}} Var[X] \\
Var[X+Y] = & Var[X] + Var[Y]
E[aX] = a E[X] \\
E[X+Y] = E[X] + E[Y] \\
Var[aX] = a^{\tiny{2}} Var[X] \\
Var[X+Y] = Var[X] + Var[Y]
\end{align*}}}}
|}}
@@ -43,9 +43,9 @@
{{{#!latex
\begin{align*}
Var[S_k] & = & Var[X_1 + X_2 + . . . +X_k] \\
& = & Var[X_1] + Var[X_2] + \dots + Var[X_k] \\
& = & k * \sigma^2
Var[S_k] & = Var[X_1 + X_2 + . . . +X_k] \\
& = Var[X_1] + Var[X_2] + \dots + Var[X_k] \\
& = k * \sigma^2
\end{align*}}}}
@@ -55,9 +55,9 @@
{{{#!latex
\begin{align*}
E[A_k] & = & E[\frac{S_k}{k}] \\
& = & \frac{1}{k}*E[S_k] \\
& = & \frac{1}{k}*k*\mu = \mu
E[A_k] & = E[\frac{S_k}{k}] \\
& = \frac{1}{k}*E[S_k] \\
& = \frac{1}{k}*k*\mu = \mu
\end{align*}}}}
@@ -65,107 +65,147 @@
{{{#!latex
\begin{align*}
Var[A_k] & = & Var[\frac{S_k}{k}] \\
& = & \frac{1}{k^2} Var[S_k] \\
& = & \frac{1}{k^2}*k*\sigma^2 \\
& = & \frac{\sigma^2}{k} \nonumber
Var[A_k] & = Var[\frac{S_k}{k}] \\
& = \frac{1}{k^2} Var[S_k] \\
& = \frac{1}{k^2}*k*\sigma^2 \\
& = \frac{\sigma^2}{k} \nonumber
\end{align*}}}}
라고 할 수 있다.
라고 할 수 있다.
한편, 분산값은
{{{#!latex
\begin{align*}
Var[X] & = & E{(X-\mu)^2} \\
& = & E[(X^2 - 2 X \mu + \mu^2)] \\
& = & E[X^2] - 2 \mu E[X] + E[\mu^2] \\
& = & E[X^2] - 2 \mu E[X] + E[\mu^2], \;\; \text{because E[X]=} \mu \text{, \; E[} \mu^2 \text{] = } \mu^2, \\
& = & E[X^2] - 2 \mu^2 + \mu^2 \\
& = & E[X^2] - \mu^2
Var[X] & = {E{(X-\mu)^2}} \\
& = E[(X^2 - 2 X \mu + \mu^2)] \\
& = E[X^2] - 2 \mu E[X] + E[\mu^2] \\
& = E[X^2] - 2 \mu E[X] + E[\mu^2], \;\; \text{because E[X]=} \mu \text{, \; E[} \mu^2 \text{] = } \mu^2, \\
& = E[X^2] - 2 \mu^2 + \mu^2 \\
& = E[X^2] - \mu^2 \;\;\; \dots \dots \dots \dots \dots [1]
\end{align*}}}}
$E[X]=a \;\; E[Y]=b$ 라고 하면
라고 할때,
$ Var[X + Y] $ 를 구하고자 한다면, 우선
{{{#!latex
\begin{align}
\displaystyle E[X] = \mu_{X} = a \\
\displaystyle E[Y] = \mu_{Y} = b
\end{align}
}}}
이라고 할 때,
{{{#!latex
\begin{align*}
Var[X+Y] & = & E[(X+Y)^2] - (a+b)^2 \\
& = & E[(X^2 + 2XY + Y^2)] - (a^2 - 2ab - b^2) \;\cdots\;\cdots\; [a]
Var [X + Y] & = \displaystyle E[(X+Y)^2] - (a+b)^2 \\
& = E[(X^2 + 2XY + Y^2)] - (a^2 - 2ab - b^2) \;\cdots\;\cdots\; \cdots\; [a]
\end{align*}}}}
그런데 $E[XY] = E[X] E[Y], $ , $X$ 와 $Y$ 가 independent이므로
그런데
$ E[XY] = E[X] E[Y], $ , $X$ 와 $Y$ 가 서로 독립적 (independent) 이므로
$ E[XY] = a b $
이에 따라 위의 $ [a] $ 에서,
{{{#!latex
\begin{align*}
Var[X+Y] & = & E[(X^2 + 2XY + Y^2)] - (a^2 - 2ab - b^2) \\
& = & E[(X^2-a^2 + Y^2-b^2)] \\
& = & Var[X] + Var[Y]
Var [X + Y] & = E[(X^2 + 2XY + Y^2)] - (a^2 - 2ab - b^2) \\
& = E[X^2] - a^2 + E[Y^2] - b^2 \\
& = Var[X] + Var[Y]
\end{align*}
}}}
한편,
{{{#!latex
\begin{align*}
\overline{X} & = \frac { \displaystyle \sum_{i=1}^n (X_i)} {n} \\
s_{\overline{X}} & = \frac {\displaystyle \sum_{i=1}^n (X_i - \overline{X})^2} {n-1}
\end{align*}}}}
그리고 Sampling distribution of mean과 관련된 샘플 평균들에 대한 기대값 $E[\overline{X}]$ 과 $Var[\overline{X}]$ 는 각각
{{{#!latex
\begin{align*}
E[\overline{X}] & = & E[\frac{1}{n} \sum_{\tiny{i=1}}^{\tiny{n}} \overline{X_i}] \\
& = & \frac{1}{n} n \mu \\
& = & \mu \;\cdots\;\cdots\;\cdots\;\cdots \;[2] \\
Var[\overline{X}] & = & Var[\frac{1}{n} \sum_{\tiny{i=1}}^{\tiny{n}} \overline{X_i}] \\
& = & \frac{1}{n^2} n \sigma^2 \\
& = & \frac{\sigma^2}{n} \;\cdots\;\cdots\;\cdots\;\cdots \;
E[\overline{X}] & = E[\frac{1}{n} \sum_{\tiny{i=1}}^{\tiny{n}} \overline{X_i}] \\
& = \frac{1}{n} n \mu \\
& = \mu \;\cdots\;\cdots\;\cdots\;\cdots \;[2] \\
Var[\overline{X}] & = Var[\frac{1}{n} \sum_{\tiny{i=1}}^{\tiny{n}} \overline{X_i}] \\
& = \frac{1}{n^2} n \sigma^2 \\
& = \frac{\sigma^2}{n} \;\cdots\;\cdots\;\cdots\;\cdots \;[3]
\end{align*}}}}
같은 논리로 sampling distribution of samle variance를 구한다고 하면, 그리고 이를 구할 때 n을 사용한다고 하면,
같은 논리로 sampling distribution of sample variance를 구한다고 하면, 그리고 이를 구할 때 n을 사용한다고 하면,
\begin{align*}
E[S^2] & = & E \left [ \frac{1}{\large n} \sum_{i=1}^n (X_i- \overline{X})^2 \right ] \\
& = & \frac{1}{\large n} E \left [ \sum_{i=1}^n (X_i^2 - 2\overline{X}X_i + \overline{X}^2) \right ] \\
& = & \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - \sum_{i=1}^n 2\overline{X}X_i + \sum_{i=1}^n \overline{X}^2 \right ] \\
& = & \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - 2n\overline{X}^2 +n\overline{X}^2 \right ] \\
& = & \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - n\overline{X}^2 \right ] \\
& = & \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 \right ] - E \left [ \overline{X}^2 \right ] \;\cdots\;\cdots\; [4]
E[s^2] & = E \left [ \frac{1}{\large n} \sum_{i=1}^n (X_i- \overline{X})^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n (X_i^2 - 2\overline{X}X_i + \overline{X}^2) \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - \sum_{i=1}^n 2\overline{X}X_i + \sum_{i=1}^n \overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - 2n\overline{X}^2 +n\overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - n\overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 \right ] - E \left [ \overline{X}^2 \right ] \;\cdots\;\cdots\; [4]
\end{align*}}}}
\begin{align*}
\sum 2 X_i \overline{X} & = & 2 \overline{X} n \overline{X} \\
& = & 2n \overline{X}^2 \nonumber
\sum 2 X_i \overline{X} & = 2 \sum X_i \overline{X} \\
& = 2 n \overline{X} * \overline{X} \;\; \text {because} \;\; \overline{X} = \frac {\sum X_i} {n} \;\;\\
& = 2 n \overline{X}^2
\end{align*}}}}
$E \left [ \overline{X}^2 \right ] = Var \left [\overline{X}^2 \right ] + \mu = \frac{\sigma^2}{n} + \mu $ 이므로 [4]의 식은
$ E \left [ \displaystyle \sum_{i=1}^n X_i^2 \right ] = Var[X_i] + \mu = \sigma^2 + \mu$
$ E \left [ \displaystyle \overline{X}^2 \right ] = Var \left [\overline{X} \right ] + \mu = \frac{\sigma^2}{n} + \mu $ 이므로 [4]의 식은
{{{#!latex
\begin{align*}
E[s^2] & = & \frac{1}{n} (\sigma^2+\mu) - ( \frac{\sigma^2}{n} + \mu) \\
& = & \frac{1}{n} \left [n(\sigma^2+\mu) - n(\frac{\sigma^2}{n} + \mu) \right ] \\
& = & \frac{1}{n} \left [n \sigma^2 - \sigma^2 \right ] \\
& = & \frac{(n-1)\sigma^2}{n} \;\cdots\;\cdots\;\cdots\; [5]
E[s^2] & = \frac{1}{n} (\sigma^2+\mu) - ( \frac{\sigma^2}{n} + \mu) \\
& = \frac{1}{n} \left [n(\sigma^2+\mu) - n(\frac{\sigma^2}{n} + \mu) \right ] \\
& = \frac{1}{n} \left [n \sigma^2 - \sigma^2 \right ] \\
& = \frac{(n-1)\sigma^2}{n} \;\cdots\;\cdots\;\cdots\; [5]
\end{align*}}}}
$E[S^2] = \frac{(n-1)\sigma^2}{n} * \frac{n}{n-1} = \sigma^2 $
$ \displaystyle \frac{n}{n-1} $
을 [5]에 곱하면,
$ E[S^2] = \displaystyle \frac{(n-1)\sigma^2}{n} * \frac{n}{n-1} = \sigma^2 $
----
CategoryResearchMethods
- See Also
 Variance
Variance
Estimated value of SD ¶
우선, Expected value (기대값)와 Variance (분산)의 연산은 아래와 같이 계산될 수 있다.
X,Y are Independent variables.
이때, 한 샘플의 평균값을 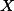 라고 하면, 평균들의 합인
라고 하면, 평균들의 합인 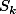 는
는
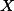 라고 하면, 평균들의 합인
라고 하면, 평균들의 합인 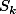 는
는 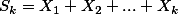
이렇게 얻은 샘플들(k 개의)의 평균인 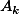 는,
는,
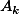 는,
는, 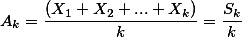
이때,
![\begin{align*}
E[S_k] & = E[X_1 + X_2 + . . . +X_k] \\
& = E[X_1] + E[X_2] + . . . + E[X_k] \\
& = \mu + \mu + . . . + \mu = k * \mu \\
\end{align*}
\begin{align*}
E[S_k] & = E[X_1 + X_2 + . . . +X_k] \\
& = E[X_1] + E[X_2] + . . . + E[X_k] \\
& = \mu + \mu + . . . + \mu = k * \mu \\
\end{align*}](/_cache/latex/f/ff/df52295b6000fa1ec397651d09e87b75.png)
![\begin{align*}
Var[S_k] & = Var[X_1 + X_2 + . . . +X_k] \\
& = Var[X_1] + Var[X_2] + \dots + Var[X_k] \\
& = k * \sigma^2
\end{align*}
\begin{align*}
Var[S_k] & = Var[X_1 + X_2 + . . . +X_k] \\
& = Var[X_1] + Var[X_2] + \dots + Var[X_k] \\
& = k * \sigma^2
\end{align*}](/_cache/latex/4/41/4645b4290649bfc304c7f5e647aacd4b.png)
이다.
그렇다면, 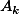 에 관한 기대값과 분산값은:
에 관한 기대값과 분산값은:
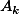 에 관한 기대값과 분산값은:
에 관한 기대값과 분산값은: ![\begin{align*}
E[A_k] & = E[\frac{S_k}{k}] \\
& = \frac{1}{k}*E[S_k] \\
& = \frac{1}{k}*k*\mu = \mu
\end{align*}
\begin{align*}
E[A_k] & = E[\frac{S_k}{k}] \\
& = \frac{1}{k}*E[S_k] \\
& = \frac{1}{k}*k*\mu = \mu
\end{align*}](/_cache/latex/3/37/ce69a40645db99b5543d3f72a19e2698.png)
이고,
![\begin{align*}
Var[A_k] & = Var[\frac{S_k}{k}] \\
& = \frac{1}{k^2} Var[S_k] \\
& = \frac{1}{k^2}*k*\sigma^2 \\
& = \frac{\sigma^2}{k} \nonumber
\end{align*}
\begin{align*}
Var[A_k] & = Var[\frac{S_k}{k}] \\
& = \frac{1}{k^2} Var[S_k] \\
& = \frac{1}{k^2}*k*\sigma^2 \\
& = \frac{\sigma^2}{k} \nonumber
\end{align*}](/_cache/latex/7/7f/72c07276f88b0d7c93a38c28716d0ae7.png)
라고 할 수 있다.
한편, 분산값은
![\begin{align*}
Var[X] & = {E{(X-\mu)^2}} \\
& = E[(X^2 - 2 X \mu + \mu^2)] \\
& = E[X^2] - 2 \mu E[X] + E[\mu^2] \\
& = E[X^2] - 2 \mu E[X] + E[\mu^2], \;\; \text{because E[X]=} \mu \text{, \; E[} \mu^2 \text{] = } \mu^2, \\
& = E[X^2] - 2 \mu^2 + \mu^2 \\
& = E[X^2] - \mu^2 \;\;\; \dots \dots \dots \dots \dots [1]
\end{align*}
\begin{align*}
Var[X] & = {E{(X-\mu)^2}} \\
& = E[(X^2 - 2 X \mu + \mu^2)] \\
& = E[X^2] - 2 \mu E[X] + E[\mu^2] \\
& = E[X^2] - 2 \mu E[X] + E[\mu^2], \;\; \text{because E[X]=} \mu \text{, \; E[} \mu^2 \text{] = } \mu^2, \\
& = E[X^2] - 2 \mu^2 + \mu^2 \\
& = E[X^2] - \mu^2 \;\;\; \dots \dots \dots \dots \dots [1]
\end{align*}](/_cache/latex/1/12/db47bdbe19a86d6e9d0397428fec7d0a.png)
라고 할때,
![$ Var[X + Y] $ $ Var[X + Y] $](/_cache/latex/c/c3/053b4d37da525adc41dbd9a1ae2f3af4.png) 를 구하고자 한다면, 우선
를 구하고자 한다면, 우선 ![\begin{align}
\displaystyle E[X] = \mu_{X} = a \\
\displaystyle E[Y] = \mu_{Y} = b
\end{align}
\begin{align}
\displaystyle E[X] = \mu_{X} = a \\
\displaystyle E[Y] = \mu_{Y} = b
\end{align}](/_cache/latex/d/dc/42496fc45817370a87be98ff9485e57d.png)
이라고 할 때,
![\begin{align*}
Var [X + Y] & = \displaystyle E[(X+Y)^2] - (a+b)^2 \\
& = E[(X^2 + 2XY + Y^2)] - (a^2 - 2ab - b^2) \;\cdots\;\cdots\; \cdots\; [a]
\end{align*}
\begin{align*}
Var [X + Y] & = \displaystyle E[(X+Y)^2] - (a+b)^2 \\
& = E[(X^2 + 2XY + Y^2)] - (a^2 - 2ab - b^2) \;\cdots\;\cdots\; \cdots\; [a]
\end{align*}](/_cache/latex/f/f8/643a446db6aaa221e5f233f33ffd38a6.png)
그런데
![$ E[XY] = E[X] E[Y], $ $ E[XY] = E[X] E[Y], $](/_cache/latex/a/af/55517045fff6b916aeac670ffd5b945d.png) ,
, 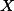 와
와 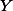 가 서로 독립적 (independent) 이므로
가 서로 독립적 (independent) 이므로 ![$ E[XY] = a b $ $ E[XY] = a b $](/_cache/latex/1/1b/be018048d9101953a0041bdff7f1821d.png)
이에 따라 위의 ![$ [a] $ $ [a] $](/_cache/latex/1/18/bc7c1963d47608f899ede881746e2aca.png) 에서,
에서,
![$ [a] $ $ [a] $](/_cache/latex/1/18/bc7c1963d47608f899ede881746e2aca.png) 에서,
에서,![\begin{align*}
Var [X + Y] & = E[(X^2 + 2XY + Y^2)] - (a^2 - 2ab - b^2) \\
& = E[X^2] - a^2 + E[Y^2] - b^2 \\
& = Var[X] + Var[Y]
\end{align*}
\begin{align*}
Var [X + Y] & = E[(X^2 + 2XY + Y^2)] - (a^2 - 2ab - b^2) \\
& = E[X^2] - a^2 + E[Y^2] - b^2 \\
& = Var[X] + Var[Y]
\end{align*}](/_cache/latex/f/f9/ae1f28a56921a9b8bc98ed0edce54f59.png)
한편,

그리고 Sampling distribution of mean과 관련된 샘플 평균들에 대한 기대값 ![$E[\overline{X}]$ $E[\overline{X}]$](/_cache/latex/1/16/62ed1eb86d4cfd41a9cae82d727362bd.png) 과
과 ![$Var[\overline{X}]$ $Var[\overline{X}]$](/_cache/latex/7/70/41a6322d034a295c0a306cfcab60207a.png) 는 각각
는 각각
![$E[\overline{X}]$ $E[\overline{X}]$](/_cache/latex/1/16/62ed1eb86d4cfd41a9cae82d727362bd.png) 과
과 ![$Var[\overline{X}]$ $Var[\overline{X}]$](/_cache/latex/7/70/41a6322d034a295c0a306cfcab60207a.png) 는 각각
는 각각![\begin{align*}
E[\overline{X}] & = E[\frac{1}{n} \sum_{\tiny{i=1}}^{\tiny{n}} \overline{X_i}] \\
& = \frac{1}{n} n \mu \\
& = \mu \;\cdots\;\cdots\;\cdots\;\cdots \;[2] \\
Var[\overline{X}] & = Var[\frac{1}{n} \sum_{\tiny{i=1}}^{\tiny{n}} \overline{X_i}] \\
& = \frac{1}{n^2} n \sigma^2 \\
& = \frac{\sigma^2}{n} \;\cdots\;\cdots\;\cdots\;\cdots \;[3]
\end{align*}
\begin{align*}
E[\overline{X}] & = E[\frac{1}{n} \sum_{\tiny{i=1}}^{\tiny{n}} \overline{X_i}] \\
& = \frac{1}{n} n \mu \\
& = \mu \;\cdots\;\cdots\;\cdots\;\cdots \;[2] \\
Var[\overline{X}] & = Var[\frac{1}{n} \sum_{\tiny{i=1}}^{\tiny{n}} \overline{X_i}] \\
& = \frac{1}{n^2} n \sigma^2 \\
& = \frac{\sigma^2}{n} \;\cdots\;\cdots\;\cdots\;\cdots \;[3]
\end{align*}](/_cache/latex/2/22/aa02dc2114cbb69619f40df27dd5b971.png)
같은 논리로 sampling distribution of sample variance를 구한다고 하면, 그리고 이를 구할 때 n을 사용한다고 하면,
![\begin{align*}
E[s^2] & = E \left [ \frac{1}{\large n} \sum_{i=1}^n (X_i- \overline{X})^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n (X_i^2 - 2\overline{X}X_i + \overline{X}^2) \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - \sum_{i=1}^n 2\overline{X}X_i + \sum_{i=1}^n \overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - 2n\overline{X}^2 +n\overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - n\overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 \right ] - E \left [ \overline{X}^2 \right ] \;\cdots\;\cdots\; [4]
\end{align*}
\begin{align*}
E[s^2] & = E \left [ \frac{1}{\large n} \sum_{i=1}^n (X_i- \overline{X})^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n (X_i^2 - 2\overline{X}X_i + \overline{X}^2) \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - \sum_{i=1}^n 2\overline{X}X_i + \sum_{i=1}^n \overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - 2n\overline{X}^2 +n\overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 - n\overline{X}^2 \right ] \\
& = \frac{1}{\large n} E \left [ \sum_{i=1}^n X_i^2 \right ] - E \left [ \overline{X}^2 \right ] \;\cdots\;\cdots\; [4]
\end{align*}](/_cache/latex/7/75/47872bb261b2600391341e619c9115af.png)
위에서
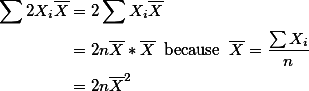
여기서 1에서의 결과를 적용하면,
![\begin{align*}
E[s^2] & = \frac{1}{n} (\sigma^2+\mu) - ( \frac{\sigma^2}{n} + \mu) \\
& = \frac{1}{n} \left [n(\sigma^2+\mu) - n(\frac{\sigma^2}{n} + \mu) \right ] \\
& = \frac{1}{n} \left [n \sigma^2 - \sigma^2 \right ] \\
& = \frac{(n-1)\sigma^2}{n} \;\cdots\;\cdots\;\cdots\; [5]
\end{align*}
\begin{align*}
E[s^2] & = \frac{1}{n} (\sigma^2+\mu) - ( \frac{\sigma^2}{n} + \mu) \\
& = \frac{1}{n} \left [n(\sigma^2+\mu) - n(\frac{\sigma^2}{n} + \mu) \right ] \\
& = \frac{1}{n} \left [n \sigma^2 - \sigma^2 \right ] \\
& = \frac{(n-1)\sigma^2}{n} \;\cdots\;\cdots\;\cdots\; [5]
\end{align*}](/_cache/latex/8/80/6168fce0b311fa00d08e255d1bd22288.png)
즉 sample에서 구하는 variance로 모집단의 variance를 구하는데 오차가 보인다. 이를 모집단의 variance와 근사하게 하기 위해서
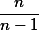
을 5에 곱하면,
![$ E[S^2] = \displaystyle \frac{(n-1)\sigma^2}{n} * \frac{n}{n-1} = \sigma^2 $ $ E[S^2] = \displaystyle \frac{(n-1)\sigma^2}{n} * \frac{n}{n-1} = \sigma^2 $](/_cache/latex/b/bb/e571448d5bb6c7d25919946a4e1d49ef.png)



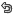




![$ E \left [ \displaystyle \sum_{i=1}^n X_i^2 \right ] = Var[X_i] + \mu = \sigma^2 + \mu$ $ E \left [ \displaystyle \sum_{i=1}^n X_i^2 \right ] = Var[X_i] + \mu = \sigma^2 + \mu$](/_cache/latex/4/4e/80b84237233461e09bab0d26f1096f67.png)
![$ E \left [ \displaystyle \overline{X}^2 \right ] = Var \left [\overline{X} \right ] + \mu = \frac{\sigma^2}{n} + \mu $ $ E \left [ \displaystyle \overline{X}^2 \right ] = Var \left [\overline{X} \right ] + \mu = \frac{\sigma^2}{n} + \mu $](/_cache/latex/9/97/3c59916f6e944a16e3af24c5d37f158b.png) 이므로
이므로 