Communication Research: Absolute Value Of Deviation Score

Communication Research

Wikipage

FrontPage › AbsoluteValueOfDeviationScore

Absolute Value Of Deviation Score

Difference between r1.7 and the current

@@ -8,8 +8,11 @@

{{{#!latex
\begin{eqnarray*}
\text{SS} & = & \small{\sum} \normal (X_i-\overline{X})^2 \\

\text{. . . .}

& = & ~~\small~~{\sum} \normal X_i^2 - \frac{(\small{\sum}\normal{X_i)^2}}{n} ~~\;\cdots\; \text{cause } \overline{X}=\frac{\small\sum \normal X_i}{n} \;\; [2]~~

& = & \text{. . . .} \\

& = & {\sum} \normal X_i^2 - \frac{(\small{\sum}\normal{X_i)^2}}{n}

\end{eqnarray*}
}}}
See http://wiki.commres.org/ANOVA#s-2.2

1. 실제로 Mean absolute deviation (MAD) 으로 사용되고 있기도 하다. see [WikiPedia:Average_absolute_deviation Average Absolute Deviation]

1. See [http://stats.stackexchange.com/questions/118/why-square-the-difference-instead-of-taking-the-absolute-value-in-standard-devia Cross Validated에서 나온 질문과 답]

왜 차이값을 (deviation score) 제곱하여 더한 값의 평균 (즉, 분산 Variance) 을 사용하나요? 차이값의 절대값을 더한 값의 평균을 사용하는 것이 더 직관적이지 않나요?

$\text{absolute value of deviation score} = \displaystyle \frac {\sum |(X_i-\mu)| }{N}$

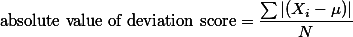
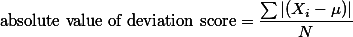
우선, raw data에서 분산값을 계산하기가 쉽다.
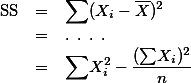$\begin{eqnarray*} \text{SS} & = & \small{\sum} \normal (X_i-\overline{X})^2 \\ & = & \text{. . . .} \\ & = & {\sum} \normal X_i^2 - \frac{(\small{\sum}\normal{X_i)^2}}{n} \end{eqnarray*}$ See http://wiki.commres.org/ANOVA#s-2.2
실제로 Mean absolute deviation (MAD) 으로 사용되고 있기도 하다. see Average Absolute Deviation
See Cross Validated에서 나온 질문과 답