Difference between r1.22 and the current
@@ -3,21 +3,18 @@
어떤 모집단에서 샘플을 취하였다면, 그 샘플의 평균과 분산 값은 그 모집단의, 그것들과 일치할 수는 없지만, 비슷해야 할 것이다. 따라서, 흔히 우리는 샘플의 평균과 분산값을 가지고 모집단의 그것을 추정하게 된다. 모집단의 분산을 구하는 공식은 아래와 같다 ([Variance] 참조).{{{#!latex
\begin{equation}
\sigma^2 \\
= \frac {\displaystyle \sum_{i=1}^N {(X_i-\mu)}^2}{N} \\
\end{equation}
\begin{equation*}
\sigma^2 = \frac {\displaystyle \sum_{i=1}^N {(X_i-\mu)}^2}{N}
\end{equation*}
}}}그러나, 샘플을 취하는 이유는 모집단의 성격을 잘 모르므로 이를 추정하기 위해서이다. 즉, 위의 공식은 모집단의 성격을 ([Mean]과 [Variance]) 알고 있어야 구하는데 현실은 그렇질 못한 경우가 많으므로, 아래의 공식이 흔히 쓰여지게 된다.
{{{#!latex
\begin{equation}
\begin{equation*}
s^2=\frac {\displaystyle \sum_{i=1}^{n} (X_i-\overline{X})^2} {(n-1)}\end{equation}
\end{equation*}
}}}어떤 모집단에서 샘플을 취하였다면, 그 샘플의 평균과 분산 값은 그 모집단의, 그것들과 일치할 수는 없지만, 비슷해야 할 것이다. 따라서, 흔히 우리는 샘플의 평균과 분산값을 가지고 모집단의 그것을 추정하게 된다. 모집단의 분산을 구하는 공식은 아래와 같다 (Variance 참조).
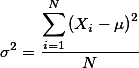
그러나, 샘플을 취하는 이유는 모집단의 성격을 잘 모르므로 이를 추정하기 위해서이다. 즉, 위의 공식은 모집단의 성격을 (Mean과 Variance) 알고 있어야 구하는데 현실은 그렇질 못한 경우가 많으므로, 아래의 공식이 흔히 쓰여지게 된다.
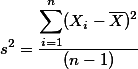
- 모집단의 평균치인  를 쓰는 대신에 샘플의 평균인
를 쓰는 대신에 샘플의 평균인  를 사용하였다는 점과
를 사용하였다는 점과
- 모집단 구성원의 숫자인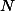 대신에 샘플의 숫자인
대신에 샘플의 숫자인 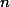 에서
에서  을 뺀,
을 뺀,  을 사용하였다는 점이다 (n-1을 사용하는 이유에 대해서는 다른 곳에서 언급을 하였다 (estimated standard deviation)).
을 사용하였다는 점이다 (n-1을 사용하는 이유에 대해서는 다른 곳에서 언급을 하였다 (estimated standard deviation)).
 를 쓰는 대신에 샘플의 평균인
를 쓰는 대신에 샘플의 평균인  를 사용하였다는 점과
를 사용하였다는 점과 - 모집단 구성원의 숫자인
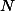 대신에 샘플의 숫자인
대신에 샘플의 숫자인 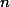 에서
에서  을 뺀,
을 뺀,  을 사용하였다는 점이다 (n-1을 사용하는 이유에 대해서는 다른 곳에서 언급을 하였다 (estimated standard deviation)).
을 사용하였다는 점이다 (n-1을 사용하는 이유에 대해서는 다른 곳에서 언급을 하였다 (estimated standard deviation)). 여기에서 사용된 n-1을 degrees of freedom 혹은 자유도라고 말한다. 자유도는 해당 샘플의 평균 값을 유지하면서 자유롭게 어떤 값을 가질 수 있는 사례 수를 말한다.
- 위에서 평균값을

- 샘플 개체의 숫자를 n이라고 가정하면,
- 샘플 개체 중 n-1개의 개체는 자유롭게 아무 값이나 가져도 되지만, 샘플의 평균인
 를 유지하기 위해서 마지막의 갯체는 어쩔 수 없는 고정값을 가져야 한다.
를 유지하기 위해서 마지막의 갯체는 어쩔 수 없는 고정값을 가져야 한다.
예를 들면 아래는 어느 한 모집단의 구성원이 한달 동안 읽는 책의 숫자를 정리한 표이다.
1, 3, 1, 4, 2, 5, 2, 2, 4, 1, 1, 4, 5, 2, 3
| Xi | ds | ds^2 | |
| 2 | -1 | 1 | |
| 3 | 0 | 0 | |
| 2 | -1 | 1 | |
| 4 | 1 | 1 | |
| 5 | 2 | 4 | |
| 5 | 2 | 4 | |
| 2 | -1 | 1 | |
| 2 | -1 | 1 | |
| 4 | 1 | 1 | |
| 1 | -2 | 4 | |
| sum | 30 | 0 | 18 |
| N | 10 | ||
| average | 3 | ||
| var | 1.8 |
위의 사례를 정리해 보면, 평균은 3, 분산은 1.8인 성격을 갖는 모집단이 된다. 이제 여기서 4개의 샘플단위를 뽑아서 샘플을 만들면 아래와 같다.
| Xi | ds | ds^2 | ||
| 2 | -1.5 | 2.25 | ||
| 5 | 1.5 | 2.25 | ||
| 3 | -0.5 | 0.25 | ||
| 4 | 0.5 | 0.25 | ||
| sum | 14 | 5 | ||
| average | 3.5 | |||
| variance | n | 4 | 1.25 | |
| variance | n-1 | 3 | 1.67 |
위에서 보면, 샘플의 평균은 3.5이고 (모집단 분산에서 사용되는 분산식을 사용한) 분산은 1.25이다. 이는 실제 모집단의 분산값인 1.8에 훨씬 못 미치는 수치이다. 그러나 n대신에 n-1로 나누어 주면, 샘플의 분산값은 1.67이 되는 이 분산 값이 모집단의 분산값에 더 가깝다. 또한 샘플의 분산값 계산에 쓰인 n-1인 3은 3개의 개체가 어떤 값을 가져도 나머지 한개의 값이 조정만된다면 전체 샘플의 평균값인 3.5를 유지할 수 있다. 다시 이야기 하면, 마지막 한 개의 값은 다른 개체와는 달리 어떤 숫자라도 가질 수 있는 자유를 잃게 된다. 따라서 우리는 이 샘플이 n-1의 자유도를 가졌다고 한다. 이 자유도는 'df'로 줄여서 많이 쓰인다.