Difference between r1.14 and the current
@@ -57,16 +57,21 @@
||... ||... ||... ||||n ||1 ||2 ||
위의 테이블을 간단히 정리하자면,
위의 데이터 테이블을 간단히 정리하자면, 위의 집단 간 평균을 구해서 기록하는 방법으로는 잘 안된다. 왜냐하면, 두 변인이 모두 종류변인 (Nominal variable)이기 때문이다. 종류의 변인이 정리가 되는 경우, 대개는 빈도수가 사용된다.
|||| |||| 이타심 ||
|||| || 있음 || 없음 ||||<valign="middle"><|2>성 || male || || ||
|| female || || ||
||<valign="middle"><|2>성 || male || 15 || 35 ||
|| female || 40 || 10 ||
이제 위의 테이블을 보고 연구자는 성별의 차이가 이타심의 존재 유무에 영향을 미치는가에 대한 판단을 해야 한다. 남들에게 가장 확신을 주는 테이블은 아마도 아래와 같은 경우일 것이다.
|||| |||| 이타심 ||
|||| || 있음 || 없음 ||
||<valign="middle"><|2>성 || male || || 50 ||
|| female || 50 || ||
그렇지만 현실적으로 이런 상태의 데이터를 얻을 수는 없을 것이다. 따라서 연구자는 위의 테이블의 결과를 가지고 남성과 여성 사이에서 이타심은 서로 다르게 나타난다고 판단해야 한다.
== Hypothesis testing ==
Hypothesis test란, 샘플을 이용한 통계학 방법을 가르키는 말로서, 모집단의 성격에 대한 가설을 평가하는 작업을 말한다.
1. Introduction ¶
가설에는 차이와 관련을 나타내는 것이 있다고 하였다 (Hypothesis 참조). 가설에 나타나는 IV 와 DV 가 어떻게 측정(measure)이 되었는가에 따라서 차이와 관련의 가설로 나누게 된다. 아래 가설들은 각각의 변인(독립, 종속변인)들이 어떻게 측정되었는가에 따라서 예를 들기 위해 만들어진 것이다.
독립변인=종류변인 :: 종속변인=숫자변인 인 경우:
가설1] 여성과 남성 간의 수학점수에는 차이가 있을 것이다.
위의 가설관 관련된 변인은 성(gender)과 수학점수(math score) 이 있다. 전자는 독립변인(IV) 후자는 종속변인(DV)으로 볼 수 있다 (variable identification 참조). 각각의 변인은 어떻게 측정되어야 할까? 이 가설의 경우에는 쉽다.
--위의 가설관 관련된 변인은 성(gender)과 수학점수(math score) 이 있다. 전자는 독립변인(IV) 후자는 종속변인(DV)으로 볼 수 있다 (variable identification 참조). 각각의 변인은 어떻게 측정되어야 할까? 이 가설의 경우에는 쉽다.
성: 남/여 Gender: Male / Female ==> 종류변인 (Nominal)
수학점수: 0-100 점 사이의 점수 ==> 숫자변인 (Interval)
수학점수: 0-100 점 사이의 점수 ==> 숫자변인 (Interval)
- 위의 측정을 위해서 연구자인 당신이 해야할 일은 무엇인가? --> 사람을 구하는 것이다. 이를 샘플이라고 한다.
- 사람을 구하여 측정해야 하는 것은 무엇인가? --> 성과 수학점수이다.
- 위에서 얻은 측정치의 집합을 데이터라고 한다. 데이터를 어떻게 정리해서 기록해두어야 하는가?
위에서처럼 데이터는 변인을 항목으로 하여 각각의 케이스(사람)에 대한 측정값을 기록하는 형태로 정리되어야 한다.일련번호(기록할 필요없음) 변인이름 변인이름 serial gender math_score 1 1 78 2 2 85 3 1 70 4 2 85 5 2 90 6 1 69 .. .. ..
- 그렇다면, 이를 훗날 독자 (혹은 당신의 보고서를 읽는 사람들) 에게는 어떤 식으로 보고를 해야 하는가? --> 위의 데이터를 그냥 (raw data라고 한다) 보여주는 것은 의미가 없다. 가설과 연관지어 이 데이터를 보여주는 형식을 생각해 보면 아래와 같은 방법이 가장 합리적이다.
gender male female math score 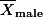
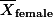 만약에 위의 실제 평균점수가 아래와 같다면,
만약에 위의 실제 평균점수가 아래와 같다면,
| gender | ||
| male | female | |
| math score | 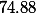 | 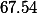 |
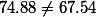 를 보여 주고, 따라서 당신이 선언한 가설이 검증되었다고 주장해야 한다. 이 예는 IV 가 종류변인(nominal)이고 DV가 숫자변인(interval)일 때 유용하다. 따라서 이를 기억하여 두도록 한다.
를 보여 주고, 따라서 당신이 선언한 가설이 검증되었다고 주장해야 한다. 이 예는 IV 가 종류변인(nominal)이고 DV가 숫자변인(interval)일 때 유용하다. 따라서 이를 기억하여 두도록 한다. 가설2] 남자와 여자 간에 이타심은 차이를 보일 것이다.
위에서 나타나는 변인들은 성(남성/여성)과 이타심이다. 성의 경우 측정은 종류변인이며 쉽게 측정될 수 있을 것으라고 생각된다. 그러나, 이타심의 경우는 좀 다르다. 우선 이타심이 정확히 무엇을 의미하는지에 대한 구체적인 근거가 없을 수 있고, 설령 있다고 해도, 다른 사람들의 머릿속에 있는 이타심과 내 머릿속의 이타심이 서로 다를 수도 있다. 이를 명확히 밝히는 작업을 개념화(Conceptualization)이라고 하였다. 또한 조작화의 문제 나타날 수 있다.
아뭏든, 이 예에서는 개념화와 조작화의 문제를 극복했다고 가정하고, 이타심이 있고 없음을 측정하였다고 하면, 아래와 같은 데이터를 얻을 것이다.
위의 데이터 테이블을 간단히 정리하자면, 위의 집단 간 평균을 구해서 기록하는 방법으로는 잘 안된다. 왜냐하면, 두 변인이 모두 종류변인 (Nominal variable)이기 때문이다. 종류의 변인이 정리가 되는 경우, 대개는 빈도수가 사용된다.
위에서 나타나는 변인들은 성(남성/여성)과 이타심이다. 성의 경우 측정은 종류변인이며 쉽게 측정될 수 있을 것으라고 생각된다. 그러나, 이타심의 경우는 좀 다르다. 우선 이타심이 정확히 무엇을 의미하는지에 대한 구체적인 근거가 없을 수 있고, 설령 있다고 해도, 다른 사람들의 머릿속에 있는 이타심과 내 머릿속의 이타심이 서로 다를 수도 있다. 이를 명확히 밝히는 작업을 개념화(Conceptualization)이라고 하였다. 또한 조작화의 문제 나타날 수 있다.
아뭏든, 이 예에서는 개념화와 조작화의 문제를 극복했다고 가정하고, 이타심이 있고 없음을 측정하였다고 하면, 아래와 같은 데이터를 얻을 것이다.
| 참여자 | 성 | 이타심 |
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 2 | 1 |
| 4 | 2 | 1 |
| 5 | 1 | 1 |
| ... | ... | ... |
| n | 1 | 2 |
위의 데이터 테이블을 간단히 정리하자면, 위의 집단 간 평균을 구해서 기록하는 방법으로는 잘 안된다. 왜냐하면, 두 변인이 모두 종류변인 (Nominal variable)이기 때문이다. 종류의 변인이 정리가 되는 경우, 대개는 빈도수가 사용된다.
| 이타심 | |||
| 있음 | 없음 | ||
| 성 | male | 15 | 35 |
| female | 40 | 10 | |
이제 위의 테이블을 보고 연구자는 성별의 차이가 이타심의 존재 유무에 영향을 미치는가에 대한 판단을 해야 한다. 남들에게 가장 확신을 주는 테이블은 아마도 아래와 같은 경우일 것이다.
| 이타심 | |||
| 있음 | 없음 | ||
| 성 | male | 50 | |
| female | 50 | ||
그렇지만 현실적으로 이런 상태의 데이터를 얻을 수는 없을 것이다. 따라서 연구자는 위의 테이블의 결과를 가지고 남성과 여성 사이에서 이타심은 서로 다르게 나타난다고 판단해야 한다.
2. Hypothesis testing ¶
Hypothesis test란, 샘플을 이용한 통계학 방법을 가르키는 말로서, 모집단의 성격에 대한 가설을 평가하는 작업을 말한다.
간단히 그 절차를 살펴 보면,
- 먼저, 모집단에 대한 가설을 선언한다. 가설은 대개 모집단의 parameter를 밝히게 된다. 예를 들면, 우리나라 사람들의 IQ 점수가 110이라고 선언하는 것이다.
- 다음으로, 모집단에서 샘플을 추출한다. 여기서 샘플이라 함은 활률적 샘플링의 방법을 사용한 샘플을 말한다 (probability sampling). 예를 들면, 확률적 샘플로 n=200의 샘플을 한국인이라는 모집단에서 골라 낸다.
- 마지막으로 그 샘플의 성격(statistics)을 가설과 비교한다. 만약에 데이터가 가설을 지지하게 되면, 가설은 실제 모집단의 성격을 제대로 나타내는 선언문이라고 결론 지을 수 있다. 그러나, 가설과 데이터가 일치하지 않는 경우에는 반대로 가설이 잘못되었다고 결론지을 수 있다.
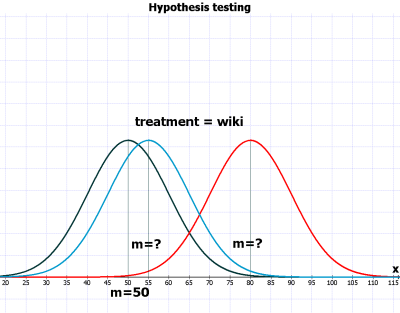
가령 예를 들면, 어느 시간 강사가 강의에 사용하는 wiki의 효과를 측정해 보기 위해서 가설 테스트(hypothesis testing)를 하는 것이다. 즉, 강사의 wiki 사용(treatment)으로 학생들의 학습효과가 높아 졌는가를 확인(test)하기 위해서 wiki를 사용한 그룹(mean=?)과 사용하지 않은 그룹 (mean=50)간의 차이를 확인해 보는 것이다 (이를 위해서 강사는 16명의 샘플을 구하였다고 가정을 하자). 위의 예에서 연구자는 wiki를 사용한 그룹의 평균이 wiki를 사용치 않은 그룹과 다르다는 것을 선언하고 이것이 통계적으로 의미가 있는가를 진단하고 결정하는 것이다.
[PNG image (39.63 KB)]
우선 연구자가 조사방법론 수업을 듣는 전체 모집단 학생들의 평균(이런 종류의 테스트가 있다고 가정)이 얼마인지를 알고 있다는 가정을 하자 (평균 = 50, stdev = 10).
연구자는 wiki를 사용하여 한 학기의 수업을 한 후에 같은 종류의 테스트를 wiki사용자들에게 하여, 이들의 평균이 wiki를 사용하지 않는 평범한 학생들의 성적과 차이가 있음을 밝힌다면, 가설검증이 성공된다.
이를 위해서 흔히 연구자는 null hypothesis를 세우게 되는데, 이것은 아래와 같이 나타낸다.
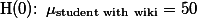
즉, 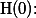 는 wiki의 사용에도 불구하고 학생들의 성적이 일반 성적인 50점에 머문다는 것을 선언하는 것이다. 다시 말하면,
는 wiki의 사용에도 불구하고 학생들의 성적이 일반 성적인 50점에 머문다는 것을 선언하는 것이다. 다시 말하면, 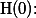 는 변화가 없음, 차이가 없음, 관계가 없음을 나타내는 선언문이다. 이를 풀어서 말하자면, wiki라는 independent variable(teatment)가 학생들의 실력(dependent variable)에 아무 효과가 없다(no effects)는 것을 나타낸다.
는 변화가 없음, 차이가 없음, 관계가 없음을 나타내는 선언문이다. 이를 풀어서 말하자면, wiki라는 independent variable(teatment)가 학생들의 실력(dependent variable)에 아무 효과가 없다(no effects)는 것을 나타낸다.
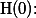 는 wiki의 사용에도 불구하고 학생들의 성적이 일반 성적인 50점에 머문다는 것을 선언하는 것이다. 다시 말하면,
는 wiki의 사용에도 불구하고 학생들의 성적이 일반 성적인 50점에 머문다는 것을 선언하는 것이다. 다시 말하면, 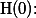 는 변화가 없음, 차이가 없음, 관계가 없음을 나타내는 선언문이다. 이를 풀어서 말하자면, wiki라는 independent variable(teatment)가 학생들의 실력(dependent variable)에 아무 효과가 없다(no effects)는 것을 나타낸다.
는 변화가 없음, 차이가 없음, 관계가 없음을 나타내는 선언문이다. 이를 풀어서 말하자면, wiki라는 independent variable(teatment)가 학생들의 실력(dependent variable)에 아무 효과가 없다(no effects)는 것을 나타낸다. alternative hypothesis 혹은 research hypothesis는 위의 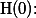 를 반대로 선언하는 것을 말한다. 위의 예를 계속 사용하자면,
를 반대로 선언하는 것을 말한다. 위의 예를 계속 사용하자면,
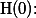 를 반대로 선언하는 것을 말한다. 위의 예를 계속 사용하자면,
를 반대로 선언하는 것을 말한다. 위의 예를 계속 사용하자면, 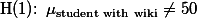
라고 선언하는 것을 말한다. 위의 선언문은 treatment인 wiki가 효과가 있다는 것을 의미한다. 단, 이 선언에서 주의해서 봐야 할 점은 wiki가 점수를 올리거나 내린다는 선언을 한 것은 아니라는 점이다. 단지 일반 population과 다를 것이라는 점만을 선언하였다.
만약에 연구자가 wiki의 사용이 학생들의 성적을 올릴 것을 확신한다면, 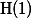 는 다음과 같이 같이 바뀌어야 한다.
는 다음과 같이 같이 바뀌어야 한다.
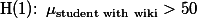
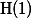 는 다음과 같이 같이 바뀌어야 한다.
는 다음과 같이 같이 바뀌어야 한다.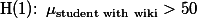
이런 종류의 research hypothesis 를 directional hypothesis라고 한다. 당분간은 이와 같은 directional hypothesis는 다루지 않겠다.
아뭏든, 앞에서 다루었듯이, 연구자는 테스트를 위해서 샘플들의 평균값들이 어떻게 분포하는 지를 살펴 볼 것이다. 이 예의 경우,
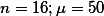 이다.
이다.이 분포는 다시 두개의 종류로 나위어서 생각될 수 있는데,
- 첫 째는 nh가 참인 경우 나올 수 있는 샘플의 평균값 범위에 포함되는 샘플평균값과
- 둘 째는, nh가 참인 경우에 나올 수 있는 샘플의 평균값 범위에 속하지 않는 샘플의 평균값이다.
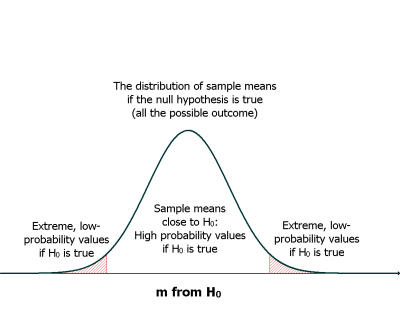
[PNG image (23.08 KB)]
이와는 반대로 양 쪽의 부분은 이 sampling distribution에서 나오기 어려운 sample mean들의 범위이다. 그런데, 이 sampling distribution 분포는 null hypothesis 가 참이라는 것을 가정했을 때 나타나는 normal distribution이므로, 만약에 wiki를 사용한 학생들의 점수가 이 범위안에서 발견된다면, wiki라는 treatment(IV)가 없었을 때에도 평범하게 나타날 수 있는 실력의 범위에서 학생들의 실력이 발견되었으므로, wiki가 효과가 없다고 이야기 할 수 있다.
만약에 이와 반대로 양 쪽 끝에서 sample의 평균점수가 발견되었다면, 이제는 평범한(IV, treatment를 받지 않은) 학생들을 모집단으로 하는 sampling distribution에서는 거의 나오지 않는 점수대(범위)에서 샘플의 평균값이 나왔으므로, 연구자는 이 샘플이 일반(평범한, IV, treatment를 받지않은) 모집단과는 다르다고 주장할 수 있는 근거가 된다. 만약에 이렇게 연구결과가 진행된다면, 연구자는 wiki의 효과가 있었다고 결론지을 것이다.
양 쪽의 rare 부분(Extreme, low-probability values if H0 is true)의 경계선은 누가 정하는가 하는 문제가 생기게 된다. 대개 연구자는 2개의 standard deviation unit을 기준으로 삼는데 이를 alpha level 혹은 level of significance이라고 한다.
2개의 standard deviation units이 의미하는 것은 위의 그림에서 빗금친 부분의 합이 5%라는 것을 의미한다. 즉, H0가 참일 때, 양 쪽의 빗금 친 부분에서 mean이 발견될 확률은 100 중 5 즉, 5%라는 의미이다. 이 빗금친 부분을 critical region이라고 한다. 다시 말하자면, 강사의 샘플의 평균값이 이 빗금친 부분에서 발견되었다면, 강사가 주장할 수 있는 것은:
... 만약에 wiki의 효과가 없었다고 하면, 이 샘플의 평균은 보통 샘플들(H0가 참인 경우의 샘플들)의 distribution 곡선에 따라서 나타나야 하는데, 빗금친 부분은 흔치 않은 경우(5%의 확률)이므로, 이 샘플은 H0이 참인 경우에 나타나는 샘플과는 다른 성격을 가진다. 즉, wiki의 효과가 있었다고 생각된다....
라는 의미의 해석을 할 것이다.
아래의 그래프는 위의 그래프를 z-score로 변환을 한것이다.
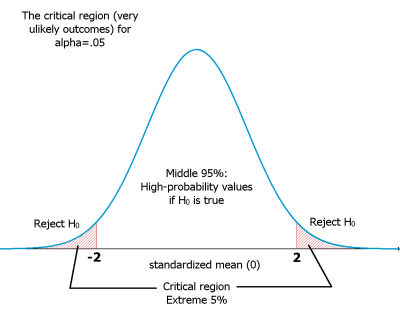

[PNG image (24.11 KB)]
이 단계에서 강사는 실제로 샘플들에게 테스트를 실시하여 샘플의 statistics를 얻어 낸 후, 이 샘플의 statistics를 H0의 것과 비교를 하게 된다. 보통 이런 비교는 z-score 변환을 통해서 한다.
sampling mean을 위한 z -score 의 공식은:
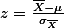
위의 공식에서  는 샘플에서 얻은 평균 값이며,
는 샘플에서 얻은 평균 값이며,  과
과 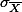 는
는 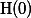 에서 얻은 것이다.
에서 얻은 것이다.
 는 샘플에서 얻은 평균 값이며,
는 샘플에서 얻은 평균 값이며,  과
과 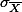 는
는 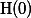 에서 얻은 것이다.
에서 얻은 것이다. 다음으로 우선 샘플의 평균값이 57.5이었다는 가정을 하면 (case A),
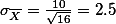
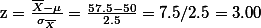
위의 경우 z-score = 3 은 z-score = 2 를 넘어서 critical region에 속하는 점수이다. 이것이 의미하는 것은 샘플의 점수가 굉장히 unusual하다는 것이고, 이를 바탕으로 강사는 샘플 학생들의 성적이 일반성적(population)보다는 다르다고 주장할 수 있다. 다시 말하면, 강사는 이제 이것을 근거로 null hypothesis를 부정(reject)하고 research hypothesis를 채택할 수 있다.
만약에 샘플의 평균값이 52.5였다고 가정을 하면 (case B),
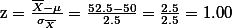
이 경우에는 z-score = 1 이고, 이는 critical region에 포함되므로, 즉, 일반학생들을 샘플링했을 때 얻을 수 있는 평균점수가 나왔으므로 wiki학생들의 점수가 일반학생들과 다르지 않다고 결론을 내릴 수 있다. 다시 말하자면, 강사는 null hypothesis를 부정(reject)하는데 실패하였다.
3. check ¶
- 이전에 CentralLimitTheorem에서 예로 든 McDonald사의 A군의 검사를 hypothesis test의 절차로 설명해 보시오.
- A: