Communication Research: Multiple regression 다중회귀

Communication Research

Wikipage

FrontPage › MultipleRegression

Multiple regression 다중회귀

1. Multiple regression
2. e.g.
3. e.g.,
4. e.g.,
5. 무엇부터? 라는 문제
6. Simple regression
7. Determining IVs' role
8. Sequential regression
9. Statistical regression

[edit]

1. Multiple regression ¶

Simple regression과 (단순회귀) mutiple regression (다중회귀) 분석은 하나의 종속변인과 다른 독립변인들(복수에 주의) 간의 관계에 대해서 살펴볼 때 사용되는 보편적인 분석방법 중의 하나이다. correlation이나 regression 이라는 용어는 보통 뚜렷한 의미차이를 두지 않고 혼용되는 경향이 많은데, 궂이 가리자면, regression은 예측 (prediction)을 하는데 많이 쓰이고, correlation은 변인간의 관계를 알아보는데 더 많이 쓰인다.

단순한 linear regression의 경우, r² 의 값에 대한 평가는 비교적 간단하다. 왜냐하면, r² 에 책임을 지는 b 값은 오직 하나이기 때문이다. Regression에서 구한 coefficient 값이 a (상수)와 b (coefficient for X)이:

Y = a + bX

라고 할때, 이 regression 공식에 대한 F 값이 통계적으로 유의미하다면, 이 값에 공헌하는 오직 하나의 변인인 X의 b값이 이에 대한 모든 것이기 때문이다. 그러나, 만약에 두 개 이상의 독립변인이 (IndependentVariable)이 regression에 사용된다면 이야기가 달라진다.

Multiple regression은 여러 연구학제에서 다양하게 사용된다, 예를 들면 Baldry [1] 는 Multiple regression방법을 이용하여 어린이들의 폭력적인 성향 (bully behavior)에 영향을 주는 요소(변인)들을 살펴보았다. Baldry는 sequential regression방법을 사용하여, 어린이의 폭력적인 행동을 설명하는 변인으로 나이와 성별(남자, 여자)를 우선 선택하였고, 두 번째 절차로 아버지의 어머니에 대한 언어적, 신체적 폭력성 (abuse, 어머니의 폭력성은 배제되었음)을 선택하였으며, 마지막으로 어머니의 아버지에 대한 언어적, 신체적 폭력성을 선택하여 단계적인 regression을 하였다. 그의 연구결과를 보면, 아버지의 폭력적인 성향은 아이의 폭력적 행위와 연관이 없었으며, 성별, 나이와 함께, 어머니의 폭력성이 더 아이들의 폭력적인 행동과 연관이 있었다. 위의 4가지 변인이 설명한 아이의 폭력적 행위에 대한 설명력은 14%에 그쳤다 (위의 문헌 참고).

Yang과 그의 동료들은 [2] 온라인게임 서비스에 대한 만족도(satisfaction)와 로열티에 영향을 주는 변인으로 게임서비스의 질(quality)과 이용료 (transaction cost), 그리고 경험에 대한 평가(가치, experiential value)을 들고 이들 간의 관계를 연구하였다. 연구 결과에 따르면, 세 변인 모두 게임 서비스에 대한 만족도에 영향을 주었으며, 만족도는 다시 로열티에 영향을 주는 것으로 밝혀졌다 (mediating effect). 이들은 IV 간의 관계도 측정할 수 있는 path analysis 방법을 분석도구로 사용하였는데, 이도 regression 방법의 한 종류이다.

Rice와 Katz는 [3] 다양해지는 휴대전화기의 서비스들에 대한 관심사에 영향을 주는 변인을 고찰하고, 그 변인들로, 인구통계학적 특성, 사회적인 요인, 그리고 이전의 유사한 테크놀로지의 사용 (여기서는 the Internet과 cell phone)을 들었다. 각각의 변인들로 제시된 요인들은 다시,

IVs

인구통계학적 특징:

Education
Martial Status
Age
Gender
Race/Ethnicity
Income

Social Factors

가족, 친구들과의 물리적인 거리
사회적인 도움 (support)
Privacy에 대한 권리
Privacy에 대한 위협

이전 테크놀로지에 대한 경험

Internet adoption/usage
Cell phone adoption/usage

Cell phone의 비디오, 텍스트 서비스들에 대한 평가

Surveillance 형 서비스
Entertainment 형 서비스
Intrumental 서비스

로 나누어졌다. 분석 결과, 이들은 gender를 제외한 인구통계학적인 요인이 세 가지 종류의 서비스에 대한 평가에 긍정적인 영향을 직, 간접적으로 미치는 것으로 파악이 되었으며, 간접적인 영향력은 사회적인 지원/도움을 매개로 하여 나타났다. 반면에 사회적인 요인의 경우에는 가족/친구와 물리적으로 가까우면서 친하게 지낼 수록 기능적인 (instrumental) 서비스 (위치추적 같은)에 호감을 보이는 것으로 나타났으며, privacy에 대해서 중요하게 생각할 수록 emergency 서비스를 긍정적으로 평가하는 것으로 나타났다. 하지만 전체적인 관점에서 보면, privacy와 관련된 요인은 Cell phone 사용에 대해 미미한 효과만을 보이는 것으로 나타났다. 마지막으로 인터넷과 cell phone 사용을 하지 않을 수록 기능적인 서비스 (위치추적과 같은 서비스)에 호감을 보이는 것으로 나타났다 [4] [5].

[edit]

2. e.g. ¶

Data set again.

DATA for regression analysis
bankaccount	income	famnum
6	220	5
5	190	6
7	260	3
7	200	4
8	330	2
10	490	4
8	210	3
11	380	2
9	320	1
9	270	3

    account       income        fammember   
 Min.   : 5   Min.   :190.0   Min.   :1.00  
 1st Qu.: 7   1st Qu.:212.5   1st Qu.:2.25  
 Median : 8   Median :265.0   Median :3.00  
 Mean   : 8   Mean   :287.0   Mean   :3.30  
 3rd Qu.: 9   3rd Qu.:327.5   3rd Qu.:4.00  
 Max.   :11   Max.   :490.0   Max.   :6.00

prediction for y values with 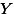$\overline{Y}$
bankaccount	error	error^2
6	-2	4
5	-3	9
7	-1	1
7	-1	1
8	0	0
10	2	4
8	0	0
11	3	9
9	1	1
9	1	1
$\overline{Y}=8$		$SS_{total} = 30$

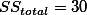Regression output (using R)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.2173 -0.5779 -0.1515  0.6642  1.1906 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept)  6.399103   1.516539   4.220  0.00394 **
fammember   -0.544727   0.226364  -2.406  0.04702 * 
income       0.011841   0.003561   3.325  0.01268 * 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

Residual standard error: 0.9301 on 7 degrees of freedom
Multiple R-squared: 0.7981,	Adjusted R-squared: 0.7404 
F-statistic: 13.84 on 2 and 7 DF,  p-value: 0.003696

$\hat{Y} = 6.399103 + (-0.544727) \text{fammember} + (0.011841) \text{income}$

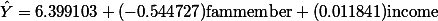
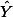위의 regression 식에 해당되는 추정치 ( $\hat{Y}$ )를 구해보면

Another X, X₂
bankaccount	pred2	error2	error²
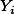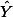$Y_{i}$	$\hat{Y}$	$\hat{Y}-Y_{i}$ = error	error²
6.000	6.281	0.281	0.079
5.000	5.381	0.381	0.145
7.000	7.844	0.844	0.712
7.000	6.588	-0.412	0.169
8.000	9.217	1.217	1.482
10.000	10.023	0.023	0.001
8.000	7.252	-0.748	0.560
11.000	9.809	-1.191	1.418
9.000	9.644	0.644	0.414
9.000	7.962	-1.038	1.077
		SS_res	6.056
		SS_reg	23.944

Still,

SS_total = 30

Now, by entering another variable X₂ = number of family, we get:

SS_unexplained = 6.056
SS_explained = 23.944

Then, R², F, b values are: ?

Model Summary(b)
Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1.000	0.893	0.798	0.740	0.930
a	Predictors: (Constant), bankfam, bankIncome income
b	Dependent Variable: bankbook number of bank

$R^2 = \frac{SS_reg}{SS_tot} =$

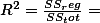
ANOVA(b)
Model		Sum of Squares	df	Mean Square	F	Sig.
1.000	Regression	23.944	2.000	11.972	13.838	0.004
	Residual	6.056	7.000	0.865
	Total	30.000	9.000
a	Predictors: (Constant), bankfam, bankIncome income
b	Dependent Variable: bankbook number of bank of bank

Coefficients(a)
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1.000	(Constant)	6.399	1.517		4.220	0.004
	bankIncome income	0.012	0.004	0.616	3.325	0.013
	bankfam	-0.545	0.226	-0.446	-2.406	0.047
a	Dependent Variable: bankbook number of bank

b에 대한 (coefficients) 유의도 테스트는 t-test를 이용하여 한다. 위의 표에서 . . . .

[edit]

3. e.g., ¶

DATA:

elemapi2.sav (28.49 KB)

	Variable Labels
Variable	Position	Label
snum	1	school number
dnum	2	district number
api00	3	api 2000
api99	4	api 1999
growth	5	growth 1999 to 2000
meals	6	pct free meals
ell	7	english language learners
yr_rnd	8	year round school
mobility	9	pct 1st year in school
acs_k3	10	avg class size k-3
acs_46	11	avg class size 4-6
not_hsg	12	parent not hsg
hsg	13	parent hsg
some_col	14	parent some college
col_grad	15	parent college grad
grad_sch	16	parent grad school
avg_ed	17	avg parent ed
full	18	pct full credential
emer	19	pct emer credential
enroll	20	number of students
mealcat	21	Percentage free meals in 3 categories
collcat	22	<none>
Variables in the working file

regression
  /dependent api00
  /method=enter ell meals yr_rnd mobility acs_k3 acs_46 full emer enroll .

	Variables Entered/Removed
Model	Variables Entered	Variables Removed	Method
1      number of students,                               Enter
       avg class size 4-6, 
       pct 1st year in school, 
       avg class size k-3, 
       pct emer credential, 
       english language learners, 
       year round school, 
       pct free meals, 
       pct full credentiala	.	
a. All requested variables entered.

Model Summary
Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1	.919a	.845	.841	56.768
a. Predictors: (Constant), number of students, avg class size 4-6, pct 1st year in school, avg class size k-3, pct emer credential, english language learners, year round school, pct free meals, pct full credential

ANOVA..b..
Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	6740702.006	9	748966.890	232.409	.000a
	Residual	1240707.781	385	3222.618
	Total	7981409.787	394
b. Dependent Variable: api 2000
a. Predictors: (Constant), number of students, avg class size 4-6, pct 1st year in school, avg class size k-3, pct emer credential, english language learners, year round school, pct free meals, pct full credential

Coefficients_a
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	758.942	62.286		12.185	.000
	english language learners	-.860	.211	-.150	-4.083	.000
	pct free meals	-2.948	.170	-.661	-17.307	.000
	year round school	-19.889	9.258	-.059	-2.148	.032
	pct 1st year in school	-1.301	.436	-.069	-2.983	.003
	avg class size k-3	1.319	2.253	.013	.585	.559
	avg class size 4-6	2.032	.798	.055	2.546	.011
	pct full credential	.610	.476	.064	1.281	.201
	pct emer credential	-.707	.605	-.058	-1.167	.244
	number of students	-.012	.017	-.019	-.724	.469
a. Dependent Variable: api 2000

[edit]

4. e.g., ¶

Another one from the same data.

REGRESSION
  /DEPENDENT api00
  /METHOD=ENTER ell acs_k3 avg_ed meals

Variable Labels
Variable	Position	Label
snum	1	school number
dnum	2	district number
api00	3	api 2000
api99	4	api 1999
growth	5	growth 1999 to 2000
meals	6	pct free meals
ell	7	english language learners
yr_rnd	8	year round school
mobility	9	pct 1st year in school
acs_k3	10	avg class size k-3
acs_46	11	avg class size 4-6
not_hsg	12	parent not hsg
hsg	13	parent hsg
some_col	14	parent some college
col_grad	15	parent college grad
grad_sch	16	parent grad school
avg_ed	17	avg parent ed
full	18	pct full credential
emer	19	pct emer credential
enroll	20	number of students
mealcat	21	Percentage free meals in 3 categories
collcat	22	<none>
Variables in the working file

Model Summary
Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1	.912a	.833	.831	58.633
a. Predictors: (Constant), pct free meals, avg class size k-3, english language learners, avg parent ed

Build a hypothesis:
What is the DV?
What are the IVs?

ANOVA(b)
Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	6393719.254	4	1598429.813	464.956	.000a
	Residual	1285740.498	374	3437.809
	Total	7679459.752	378
a. Predictors: (Constant), pct free meals, avg class size k-3, english language learners, avg parent ed
b. Dependent Variable: api 2000

What does the R² mean?
How would you make your decision on fitting the model?

Coefficients(a)
		Unstandardized Coefficients		Standardized Coefficients
Model		B	Std. Error	Beta	t	Sig.
1	(Constant)	709.639	56.240		12.618	.000
	english language learners	-.843	.196	-.147	-4.307	.000
	avg class size k-3	3.388	2.333	.032	1.452	.147
	avg parent ed	29.072	6.924	.156	4.199	.000
	pct free meals	-2.937	.195	-.655	-15.081	.000
a. Dependent Variable: api 2000

What is the contributions of each IV?
How would you compare to each other?

--> From here go to the data examination section. We will get back here soon. Outlier detection.

[edit]

5. 무엇부터? 라는 문제 ¶

그림 여기쯤 수록

Y 변량과 (전체변량) 세개의 독립변인의 설명변량 (X₁ X₂ X₃ ) 간의 관계에 대한 설명

따라서 어떤 변수를 어떻게 넣는가의 문제가 중요하게 됨.

[edit]

6. Simple regression ¶

[edit]

7. Determining IVs' role ¶

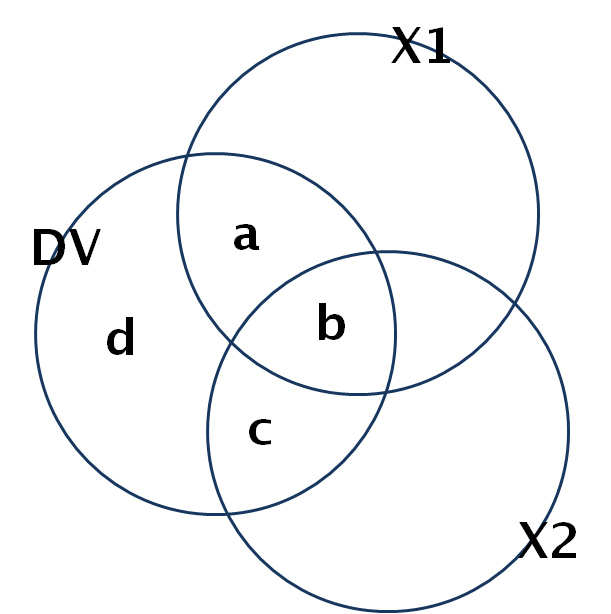
r-squared semi-partial partial correlations [JPG image (93.23 KB)]

	Standard Multiple	Sequential	comments
r_i² squared correlation	IV₁ : (a+b) / (a+b+c+d)	IV₂ : (a+b) / (a+b+c+d)	overlapped effects
	IV₂ : (c+b) / (a+b+c+d)	IV,,2: (c+b) / (a+b+c+d)
sr_i² squared semipartial correlation part in spss	IV₁ : (a) / (a+b+c+d)	IV₂ : (a+b) / (a+b+c+d)	Usual setting Unique contribution to Y
	IV₂ : (c) / (a+b+c+d)	IV₂ : (c) / (a+b+c+d)
pr_i² squared partial correlation partial in spss	IV₁ : (a) / (a+d)	IV₂ : (a+b) / (a+b+d)	Like adjusted r² Unique contribution to Y
	IV₂ : (c) / (c+d)	IV₂ : (c) / (c+d)
IV₁ 이 IV₂ 보다 먼저 투입되었을 때를 가정

Semipartial = part

주의

a+b+c+d -> 전체 Y
b -> 애매한 부분, Y에 대한 설명력의 원인으로 X₁ 이 될수도 X₂ 가 될 수도 있다.
분모부분의 차이에서 -> semipartial 과 partial 의 차이가 나타난다.
partial의 경우 -> 다른 IV의 역할이 분모, 분자에서 모두 빠져나간다.
semi-partial의 경우 --> 다른 IV의 역할이 분자에서만 빠져 나간다. 따라서 독립변인의 고유한 영향력과 종속변인의 (DV) 전체분산량 간의 비율이라고 할 수 있다. SPSS에서는 part라고 불린다.

  /STATISTICS COEFF OUTS R ANOVA CHANGE ZPP
위에서 ZPP

[edit]

8. Sequential regression ¶

SequentialRegressionAnalysis

elemapi2.sav (28.49 KB)

command line:
display labels .

			Variable Labels
Variable	Position	Label
snum	1	school number
dnum	2	district number
api00	3	api 2000
api99	4	api 1999
growth	5	growth 1999 to 2000
meals	6	pct free meals
ell	7	english language learners
yr_rnd	8	year round school
mobility	9	pct 1st year in school
acs_k3	10	avg class size k-3
acs_46	11	avg class size 4-6
not_hsg	12	parent not hsg
hsg	13	parent hsg
some_col	14	parent some college
col_grad	15	parent college grad
grad_sch	16	parent grad school
avg_ed	17	avg parent ed
full	18	pct full credential
emer	19	pct emer credential
enroll	20	number of students
mealcat	21	Percentage free meals in 3 categories
collcat	22	<none>
Variables in the working file

regression
  /dependent api00
  /method=enter ell meals yr_rnd mobility acs_k3 acs_46 full emer enroll .

vs.

regression
  /dependent api00
  /method=enter ell yr_rnd mobility acs_k3 acs_46 emer enroll 
  /method=test(meals) .

CategoryStatistics
CategoryResearchMethods
CategoryRegression

[edit]

9. Statistical regression ¶

StatisticalRegression

1. Statistical (stepwise) regression

1.1. forward selection
1.2. Backward selection
1.3. Stepwise selection

1. Statistical (stepwise) regression ¶

REGRESSION
  /DEPENDENT api00
  /METHOD=ENTER ell acs_k3 avg_ed meals .

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.	Correlations
		B	Std. Error	Beta			Zero-order	Partial	Part
1	(Constant)	709.639	56.240		12.618	.000
	ell	-.843	.196	-.147	-4.307	.000	-.766	-.217	-.091
	acs_k3	3.388	2.333	.032	1.452	.147	.185	.075	.031
	avg_ed	29.072	6.924	.156	4.199	.000	.793	.212	.089
	meals	-2.937	.195	-.655	-15.081	.000	-.902	-.615	-.319

From the left column, zero-order (r² ), partial (pr² ), and semi-partial or part (sr² ).
We know that the meal's contribution alone is the biggest in the explanation of Y variance (-.319). Then, ell, avg_ed, acs_k3.
Therefore, the beta (standardized coefficient) value of meals is the largest (We can compare the beta values across the IV since they were standardized).

1.1. forward selection ¶

Forward selection

Forward selection begins with no predictors in the regression equation. The predictor variable that has the highest correlation with the criterion variable is entered into the equation first. The rest variables are entered into the equation depending on the contribution of each predictor.
가장 큰 상관관계를 갖는 meals 변인이 먼저 투입되어 regression이 진행된다. 이 때의 zero-order r squared 값은 -.902 에 달한다. 다른 변인이 고려되지 (투입되지) 않은 상태이므로, partial, part 값들도 zero-order와 동일한 값을 갖는다.
다음 단계에서 상관관계가 다음으로 높은 변인이 투입되어 regression이 진행된다 (partial correlation값에 의해서 판단).

REGRESSION
  /DEPENDENT api00
  /METHOD=FORWARD ell acs_k3 avg_ed meals .

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.	Correlations
		B	Std. Error	Beta			Zero-order	Partial	Part
1	(Constant)	892.894	6.830		130.731	.000
	meals	-4.046	.100	-.902	-40.531	.000	-.902	-.902	-.902
2	(Constant)	887.826	6.718		132.163	.000
	meals	-3.469	.154	-.773	-22.565	.000	-.902	-.758	-.488
	ell	-.951	.197	-.166	-4.840	.000	-.766	-.242	-.105
3	(Constant)	781.172	27.182		28.738	.000
	meals	-3.004	.189	-.670	-15.855	.000	-.902	-.633	-.336
	ell	-.819	.195	-.143	-4.191	.000	-.766	-.212	-.089
	avg_ed	27.828	6.881	.149	4.044	.000	.793	.204	.086

Excluded Variablesd
Model		Beta In	t	Sig.	Partial Correlation	Collinearity Statistics
						Tolerance
1	ell	-.166a	-4.840	.000	-.242	.398
	acs_k3	.009a	.383	.702	.020	.962
	avg_ed	.175a	4.711	.000	.236	.339
2	acs_k3	.020b	.920	.358	.047	.951
	avg_ed	.149b	4.044	.000	.204	.329
3	acs_k3	.032c	1.452	.147	.075	.936

1.2. Backward selection ¶

Backward selection

Backward elimination begins with all predictor variables in the regression equation and sequentially removes them. Two removal criteria are available.

REGRESSION
  /DEPENDENT api00
  /METHOD=BACKWARD ell acs_k3 avg_ed meals .

All entered
Then, one that is not significantly contributes is removed. . . .

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.	Correlations
		B	Std. Error	Beta			Zero-order	Partial	Part
1	(Constant)	709.639	56.240		12.618	.000
	ell	-.843	.196	-.147	-4.307	.000	-.766	-.217	-.091
	acs_k3	3.388	2.333	.032	1.452	.147	.185	.075	.031
	avg_ed	29.072	6.924	.156	4.199	.000	.793	.212	.089
	meals	-2.937	.195	-.655	-15.081	.000	-.902	-.615	-.319
2	(Constant)	781.172	27.182		28.738	.000
	ell	-.819	.195	-.143	-4.191	.000	-.766	-.212	-.089
	avg_ed	27.828	6.881	.149	4.044	.000	.793	.204	.086
	meals	-3.004	.189	-.670	-15.855	.000	-.902	-.633	-.336

Excluded Variablesb
Model		Beta In	t	Sig.	Partial Correlation	Collinearity Statistics
						Tolerance
2	acs_k3	.032a	1.452	.147	.075	.936

1.3. Stepwise selection ¶

Stepwise selection

Stepwise selection is a combination of forward and backward procedures.
Step 1

The first predictor variable is selected in the same way as in forward selection. If the probability associated with the test of significance is less than or equal to the default .05, the predictor variable with the largest correlation with the criterion variable enters the equation first.

Step 2

The second variable is selected based on the highest partial correlation. If it can pass the entry requirement (PIN=.05), it also enters the equation.

Step 3

From this point, stepwise selection differs from forward selection: the variables already in the equation are examined for removal according to the removal criterion (POUT=.10) as in backward elimination.

Step 4

Variables not in the equation are examined for entry. Variable selection ends when no more variables meet entry and removal criteria.

REGRESSION
  /DEPENDENT api00
  /METHOD=STEPWISE ell acs_k3 avg_ed meals

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.	Correlations
		B	Std. Error	Beta			Zero-order	Partial	Part
1	(Constant)	892.894	6.830		130.731	.000
	meals	-4.046	.100	-.902	-40.531	.000	-.902	-.902	-.902
2	(Constant)	887.826	6.718		132.163	.000
	meals	-3.469	.154	-.773	-22.565	.000	-.902	-.758	-.488
	ell	-.951	.197	-.166	-4.840	.000	-.766	-.242	-.105
3	(Constant)	781.172	27.182		28.738	.000
	meals	-3.004	.189	-.670	-15.855	.000	-.902	-.633	-.336
	ell	-.819	.195	-.143	-4.191	.000	-.766	-.212	-.089
	avg_ed	27.828	6.881	.149	4.044	.000	.793	.204	.086

Excluded Variablesd
Model		Beta In	t	Sig.	Partial Correlation	Collinearity Statistics
						Tolerance
1	ell	-.166a	-4.840	.000	-.242	.398
	acs_k3	.009a	.383	.702	.020	.962
	avg_ed	.175a	4.711	.000	.236	.339
2	acs_k3	.020b	.920	.358	.047	.951
	avg_ed	.149b	4.044	.000	.204	.329
3	acs_k3	.032c	1.452	.147	.075	.936

CategoryResearchMethods

CategoryResearchMethods
CategoryStatistics
CategoryRegression

----

[1] Baldry, A. C. (2003). Bullying in schools and exposure to domestic violence. Child Abuse & Neglect, 27(7), 713-732. doi: doi: DOI: 10.1016/S0145-2134(03)00114-5. Bullying in schools and exposure to domestic violence.pdf (132.16 KB)
[2] Yang, H.-E., Wu, C.-C., & Wang, K.-C. (2009). An empirical analysis of online game service satisfaction and loyalty. Expert Systems with Applications, 36(2, Part 1), 1816-1825. An empirical analysis of online game service satisfaction and loyalty.pdf (259.62 KB)
[3] Rice, R. E., & Katz, J. E. (2008). Assessing new cell phone text and video services. Telecommunications Policy, 32(7), 455-467. Assessing new cell phone text and video services.pdf (249.67 KB)
[4] 관련논문: Public views of mobile medical devices and services.pdf (276.87 KB)
[5] Additional reading: Finocchiaro Castro, M. (2008). Where are you from? Cultural differences in public good experiments. Journal of Socio-Economics, 37(6), 2319-2329. Cultural differences in public good experiments.pdf (399.2 KB)

Contents

1. Multiple regression ¶

2. e.g. ¶

3. e.g., ¶

4. e.g., ¶

5. 무엇부터? 라는 문제 ¶

6. Simple regression ¶

7. Determining IVs' role ¶

8. Sequential regression ¶

9. Statistical regression ¶

Contents

1. Statistical (stepwise) regression ¶

1.1. forward selection ¶

1.2. Backward selection ¶

1.3. Stepwise selection ¶