1.1. 통계적 방법 ¶
Normality는 skewness와 kurtosis 값을 이용하여 케이스의 분포가 Normal distiribution을 따르는 가를 판단하기 위해서 사용되는 용어이다. skewness와 kurtosis 값의 standard error값을 이용하여, 유의도검사를 하게 되는데, 이때 각각의 stnadard error 값은:
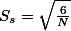
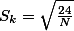 이고
이고
이를 이용하여 아래의 z-score에 대한 검증을 하게 된다.
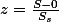
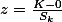
흔히, 이때의 p값은 .01 혹은 .001 의 유의도를 채택하여 검증을 한다. 이 계산을 이용할 때, 주의할 점은 샘플의 사이즈가 (N) 클때, 가설의 검증이 쉽게 이루어지는 경향이 있으므로, 전체 distribution곡선의 모양을 함께 살펴보는 것이 권장된다.
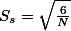
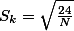 이고
이고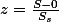
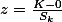
1.2. 시각적 방법 ¶
시각적인 방법으로는:
examine variables=crime /plot boxplot histogram npplot.
(1) histogram이나 boxplot을 살펴본다.
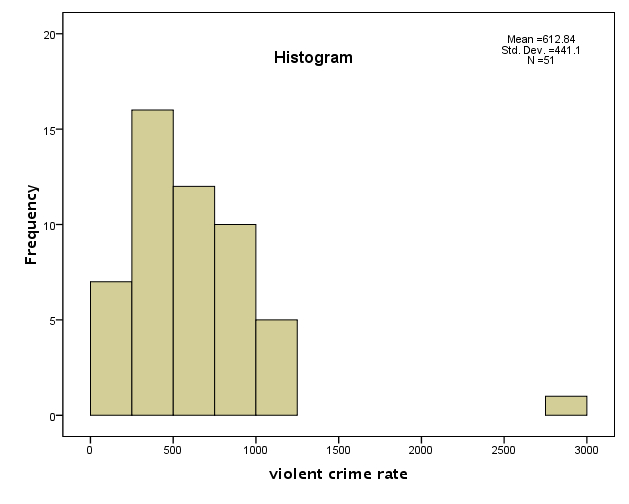
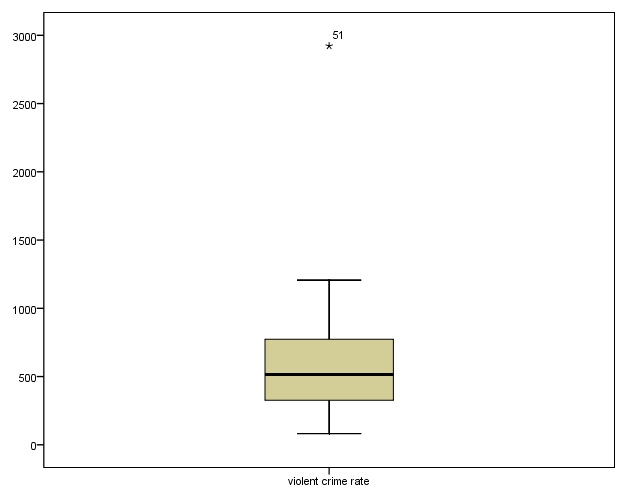
위의 예에서 유독 한 케이스만이 다른 케이스들과 동떨어져 있음을 알 수 있다.
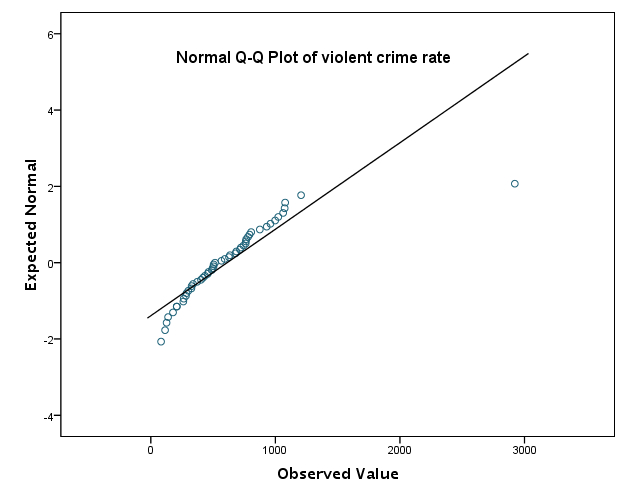
(2) normal plot을 만들어 살펴본다. 이는 데이터가 normal할 경우의 기대치를 계산한 후 기 기대치에 맞추어 실제 데이터를 나열하는 것을 말한다 (위의 명령어 참조).
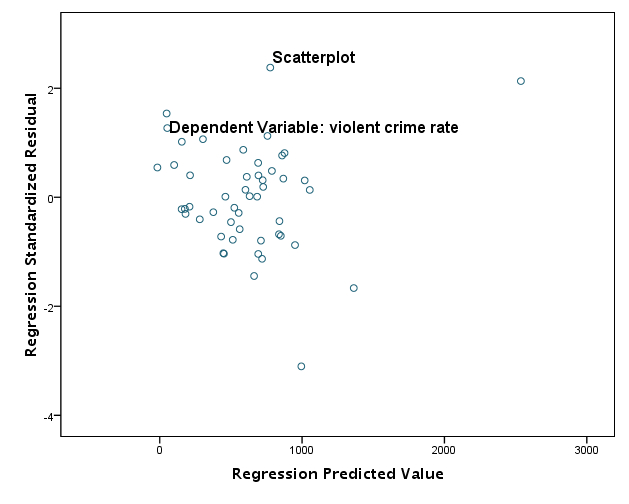
(3) Regression을 이용하여 residual(오차)의 분포를 살펴보는 방법이 있다.

Histogram [JPG image (31.15 KB)]

Boxplot [JPG image (18.1 KB)]
위의 예에서 유독 한 케이스만이 다른 케이스들과 동떨어져 있음을 알 수 있다.
(2) normal plot을 만들어 살펴본다. 이는 데이터가 normal할 경우의 기대치를 계산한 후 기 기대치에 맞추어 실제 데이터를 나열하는 것을 말한다 (위의 명령어 참조).

NNplot [JPG image (35.14 KB)]
(3) Regression을 이용하여 residual(오차)의 분포를 살펴보는 방법이 있다.
regression /dependent crime /method=enter pctmetro pctwhite poverty single /scatterplot(*zresid *pred).

scatterplot predicted value by zresiduals [JPG image (48.73 KB)]