Meaning of the standard deviation (SD):
You may be told that you don't need to remember the formula in a statistics course. However, I want you to think about what this means and remember it.
For the reference, the actual formula is:
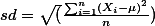
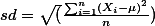
The value you get from the calculation (sd for standard deviation) is one standard deviation unit.
Now think about the word deviation. What does the word, deviation or deviate, mean? It means "variation." So, the concept behind the word, standard deviation, is that how group individual values vary. But, from what? -- from the group mean. In short, the word deviation means that how the individual values vary from the mean of the group.
Then, think about how to make this happen. The easiest thing appears to compare each value of the group elements to the value of the mean. So, if you have a group whose values are 1, 2, and 3, you compare each individual value to the mean value (which is 2, by the way). right?
Then, we might want to add them up to get the degree of deviation -- sounds reasonable, uh? One problem is that the result becomes always zero. If you don't believe me, try it for your self.
Then, what should we do about this? The solution is, we square the compared value and add them up so that we don't have to end up with the value, zero. Then, like the way you get the sample mean, you divide the result by the sample size, n (or n-1, when the group is small; but it doesn't matter). Then again, since we squared the each compared value (to the mean), the number will be somewhat big. So, we put the square root on the result. This is exactly the same as what the above formula means. It gives an idea how overall, the group units (individuals) vary to the mean of the sample.
Then, how do we interpret the value of standard deviation? Think about the above -- it gives an idea about how the group units vary to the mean. If the value is big, it means that the individual sample values vary a lot to the mean. If you want to see why:

The standard deviation can be obtained: `sd=sqrt(\sum_{i=1}^{n}(s_i-bar(x))^2/n)`. Now we can understand that if the part, `(s_i-bar(x))^2`, is big, the value of SD will be big. in other words, if individual scores of the group, `s_i` , are big or small compared to the mean value (`bar(x)`), the value of will be big. So, in order for SD to have a big value, `(s_i-bar(x))^2` should be big. This means that individual scores (`s_i`) should vary from the mean a lot. Therefore, you can guess without a mistake whose standard deviation is bigger from the below two groups.
Group A Group B 100 1 102 7 101 11 100 15 103 3 99 6 98 7
Please read the text book (p.315-318) And http://trochim.human.cornell.edu/kb/statdesc.htm
Using standard deviation -- to find out where individual score is -- depends upon an assumption of normal distribution (the Gaussian Curve; the bell curve). So, when we deal with questions like the below, we assume that we have a normal distribution curve. In other words, if the curve is skewed or too plat/peak (platokurtic/leptokurtic), using this method would not be precise.
Anyways, the main points are: IF WE HAVE A NORMAL DISTRIBUTION OF POPULATION, (1) about 68% of the population would be found in the area of "mean +- ONE standard deviation". (2) about 95% of the population would be found in the area of "mean +- TWO standard deviation". (3) about 99% of the population would be found in the area of "mean +- THREE standard devation". Please remember these characteristics. You will use it in exams.
Based on the above rules, we can guess where one particular individual score can be found in the range of population.
Suppose that the below numbers are the individual scores of the first com300 quiz.
100; 60; 40; 60; 50; 50; 30; 80; 60; 40; 0; 50; 50; 70; 60; 50; 70; 50; 80; 50; 80; 70; 50; 70; 20; 50; 30; 40; 40; 30; 50; 90; 70; 50; 70; 70; 60; 30; 70; 60; 60; 50; 70; 40; 40; 30; 70; 70; 50; 80; 40; 70; 50; 80; 40; 60; 70; 70; 80; 60; 60; 40; 50; 60; 60; 60; 30; 50; 80; 60; 70; 60; 30; 60; 50; 60; 50; 60; 70; 60; 40; 60; 30; 50; 40; 60; 70; 50; 80; 40; 50; 70; 70; 80; 40; 50; 60; 60; 50; 60; 60; 60; 50; 60; 70; 50; 60; 80; 90; 80; 50; 90; 40; 50; 60; 60; 40; 60; 50; 70; 20; 40; 60; 60; 70; 30; 50; 50; 70; 70; 60; 60; 40; 40; 80; 60; 40; 70; 50; 70; 40; 60; 60; 80; 40; 50; 40; 50; 70; 80; 40; 70; 70; 70; 70; 60; 50; 60; 60; 50; n=160 average = 56.88 variance = 245.52 Standard Deviation = 15.67

[PNG image (119.78 KB)]
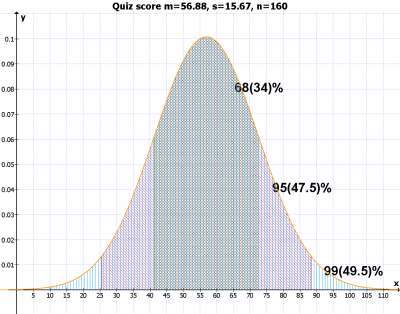
The above is the histogram of the result from the last quiz. According to the value of the standard deviation and under an assumption of normal distribution of the quiz score, We can estimate:
The numbers appearing in the three upper-right-corner cells are those corresponding "guessed percentage" when the population is normally distributed. That is, 68% of the population will be found in between mean +- one stdev; 95% in between mean +- two stdev; 99% in between mean +- three stdev. And the percentages found in the three lower-right-corner cells (67, 96, and 99%) are the actual percentages from the quiz population. as you see, they are about the same. So, if you got 80 from the quiz and know that the mean (56.88) and the standard deviation (15.67), you will be able to estimate where your score is in the big picture without actually seeing the frequency table (from the below guess).
mean (+-) 1*sd: 41.21 to 72.54 (about 50-70) --- yellow= 68% mean (+-) 2*sd: 25.54 to 88.21 (about 30-80) --- yellow(68%)+ blue(27%)= 95% mean (+-) 3*sd: 9.87 to 103.88 (about 20-100) --- yellow(68%)+ blue(27%)+ red(4%)= 99%Now, look at the frequency table:
| The below percentages are the assumptions we made from the characteristics of standard deviation. (68, 95, 99%) | |||||||
| score | frequency | percent | cumulative percent | 68% | 95% | 99% | |
| valid | 0 | 1 | 0.625 | 0.625 | |||
| 20 | 2 | 1.25 | 1.875 | 2 | |||
| 30 | 9 | 5.625 | 7.5 | 9 | 9 | ||
| 40 | 23 | 14.375 | 21.875 | 23 | 23 | ||
| 50 | 35 | 21.875 | 43.75 | 35 | 35 | 35 | |
| 60 | 41 | 25.625 | 69.375 | 41 | 41 | 41 | |
| 70 | 31 | 19.375 | 88.75 | 31 | 31 | 31 | |
| 80 | 14 | 8.75 | 97.5 | 14 | 14 | ||
| 90 | 3 | 1.875 | 99.375 | 3 | |||
| 100 | 1 | 0.625 | 100 | 1 | |||
| total | 160 | 100 | 107 | 153 | 159 | ||
| total | 160 | 100 | actual percent | 66.9% | 95.6% | 99.4% | |
| note the approx. percentage & compare these to those found in top cells | 67% (68%) | 96% (95%) | 99% (99%) | ||||
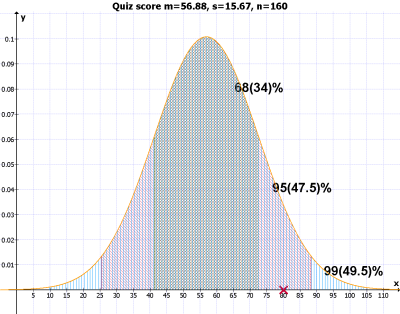
The numbers appearing in the three upper-right-corner cells are those corresponding "guessed percentage" when the population is normally distributed. That is, 68% of the population will be found in between mean +- one stdev; 95% in between mean +- two stdev; 99% in between mean +- three stdev. And the percentages found in the three lower-right-corner cells (67, 96, and 99%) are the actual percentages from the quiz population. as you see, they are about the same. So, if you got 80 from the quiz and know that the mean (56.88) and the standard deviation (15.67), you will be able to estimate where your score is in the big picture without actually seeing the frequency table (from the below guess).
mean (+-) 1sd: 41.21 to 72.54 (about 50-70) --- yellow= 68% mean (+-) 2sd: 25.54 to 88.21 (about 30-80) --- yellow(68%)+ blue(27%)= 95% mean (+-) 3sd: 9.87 to 103.88 (about 20-100) --- yellow(68%)+ blue(27%)+ red(4%)= 99%Your score is 80. So, you know that you are on the edge of the second group (see the below graph again) and also know that about 2% (that is, the half (right side) of the red area) of the students seem to have the scores higher than 80. To check your guess, you look up the frequency table and find 4 people have 90 or 100. 4 out of 160 people is about 2.5%. This is about the number you guessed (about 2%).
[PNG image (119.92 KB)]







![[http]](/imgs/http.png)

