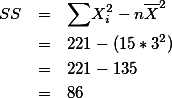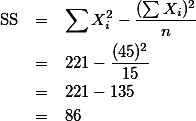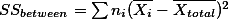GoogleTv › Project~Nrf2010/Plan › AjouWebResearchquestionnaire › Project~AjouWebResearch/Presentation › Project~Nrf2010 › ANOVA
Difference between r1.68 and the current
@@ -3,14 +3,19 @@
See also [FactorialAnova][[TableOfContents]]
= ANOVA (__AN__alysis __O__f __VA__riance), F-test =
...
[:t-test T-test] 사용은 기본적으로 두 가지면에서 한계를 갖는다. 첫째는 독립변인으로 오로지 2 그룹만을 비교할 수 없다는 것이다. (예를 들 것). 두번째로는 t test 는 오직 하나만의 독립변인을 검증한다는 것이다. (예를 들 것).
[ANOVA]는 2개 이상의 treatment 혹은 population 집단의 평균 점수를 평가하는데 쓰이는 가설 검증 절차이다. 추정통계가 (Inferential statistics) 모두 그렇듯이, ANOVA 또한 샘플의 평균값으로 모집단의 평균값을 추정하여 각 집단 간의 차이가 통계학적으로 의미가 있는지 살펴보는 절차이다. ANOVA와 T-test는 샘플 그룹 간의 평균을 비교한다는 의미에서 서로 비슷하게 보이지만, [ANOVA]는 [:t-test T-test]에 비해 월등한 이점을 가지고 있다. 특히 T-test의 경우에는 두 집단 간의 비교만 가능하지만, ANOVA는 __두개 혹은 그 이상의 집단__ 간의 평균을 비교하는것이 가능하다. 따라서 연구자는 ANOVA를 이용하여 실험이나 서베이 등을 좀 더 유연하게 디자인할 수 있다.
| ANOVA test |||||||<table class="wikiLeft"> '''ANOVA''' ||
|| 4 학년 || 5 학년 || 6 학년 ||
|| 샘플 1의 과학[[br]]지식 점수 || 샘플 2의 과학[[br]]지식 점수 || 샘플 3의 과학[[br]]지식 점수 ||
||||||||* 독립변인: 학년[[br]] * 종속변인: 과학지식 ||
T-test와 마찬가지로, ANOVA 또한 독립적인 측정으로 이루어진 집단의 비교나 (IndependentTtest) 반복 측정 (repeated measure)으로 나타나는 동일 집단의 시간차 비교에 사용될 수 있다. 독립적인 측정이라 함은 2개 이상의 treatment(처치 혹은 실험처치)나 2개 이상의 모집단에서 (예, 남자와 여자) 나타나는 상호배타적인 집단을 비교하는 것을 말한다. 즉, 반복측정은 여러가지 (두 번 이상의) 처치를 한 그룹이 시간을 두고 측정을 받는 것을 의미한다. 예를 들면, 미디어교육을 받기 전에 게임에 사용하는 시간을 5학년 아동들에게 측정을 했다면, 같은 그룹을 미디어교육을 받은 후에 '''반복측정''' 하는 것을 말한다.
[wiki:t-test T-test]와 마찬가지로, [ANOVA] 또한 독립적인 측정으로 이루어진 집단의 비교나 ([wiki:IndependentTtest Independent T-test]) 반복 측정 (repeated measure)으로 나타나는 동일 집단의 시간차 비교에 사용될 수 있다. 독립적인 측정이라 함은 2개 이상의 treatment(처치 혹은 실험처치)나 2개 이상의 모집단에서 (예, 남자와 여자) 나타나는 상호배타적인 집단을 비교하는 것을 말한다.
반면에 반복측정은 여러가지 (두 번 이상의) 처치를 한 그룹이 시간을 두고 측정을 받는 것을 의미한다. 예를 들면, 5학년 아동들을 대상으로 미디어교육을 받기 전에 게임에 사용하는 시간을 측정을 하고, 같은 그룹을 미디어교육을 받은 후에 다시 '''측정''' 하는 것을 "반복측정"이라고 한다.
[[HTML(<div class='clear'></div>)]]|Factorial design ANOVA|||||||||||<table class="wikiLeft"> Factorial design ||
@@ -21,23 +26,26 @@
||||||||||* 두 개의 독립변인: 학생 수와 교육방법 [[br]] * 하나의 종속변인: 과학지식 ||ANOVA는 또한 두 가지 이상의 독립변인의 ([Independent variable] (wiki:VariablesIdentification 참조)) 효과를 동시에 살펴보는데 사용되기도 한다. 가령, 연구자는 ANOVA를 이용하여 사용자 유저인터페이스의 종류와 (A, B, C: Independent Variable 1) 동영상의 사용 (있고 없음, Independent Variable 2)가 과학지식의 습득에 얼마나 영향을 주는지 동시에 살펴볼 수 있다.
= Factors =
위의 표에서 사용된 용어인 독립변인을 (attributes) ANOVA에서는 팩터라고 (factor) 부른다. 위의 첫 번째 표에서 처럼 하나의 독립변인이 (factor) 이용된 경우 ''single factor design'' 이라고 하며, 두 번째처럼 두 개 이상의 독립변인이 이용된 경우를 ''factorial design'' 이라고 부른다 ([[FactorialAnova]] 참조).[[HTML(<div class='clear'></div>)]]
아래의 그림은 부모의 사회경제적 지위에 따른 과학점수의 차이를 보여주는 예이다. Group1(H), Group2(M), Group3(L)의 세집단의 그룹 멤버쉽에 따라서 과학점수 ( $\small\mu_i$ )의 평균이 다를 것이라는 것이 연구자의 관심사이다.
[[Attachment(ANOVA-example.png,align=right,width=250,caption="three group comparison",selflink)]]
위의 그림에서 연구자는 전체 모집단에서 3가지의 특성을 (attributes) 가지는 하위 집단을 규정하고, 이 집단의 특성이 서로 다른가에 대한 의문을 갖는 것을 나타낸다 (그림의 위쪽 부분). 연구자는 이 상태에서 각 집단의 구성원을 모두 조사할 수는 없으므로, 각각의 특성에 일치하는 샘플을 (Sample,,1,,, Sample,,2,,, Sample,,3,,) 구하여 샘플의 평균값을 ( $\small\overline{X_i}$ ) 살펴보고, 각 평균값의 차이가 (1) 모집단의 실제 값을 대표하는지와 (2) 이 평균값의 차이가 통계학적으로 의미가 있는지를 살펴 본다. 즉, 위의 그림에서 평균값 $\small\overline{X_1}$ , $\small\overline{X_2}$ , $\small\overline{X_3}$ 의 {2, 4, 6} 간의 차이를 가지고 연구자는 두 가지 종류의 해석을 할 수 있다.
위의 그림에서 연구자는 전체 모집단에서 3가지의 특성을 (attributes) 가지는 하위 집단을 규정하고, 이 집단의 특성이 서로 다른가에 대한 의문을 갖는 것을 나타낸다 (그림의 위쪽 부분). 연구자는 이 상태에서 각 집단의 구성원을 모두 조사할 수는 없으므로, 각각의 특성에 일치하는 샘플을 (Sample,,1,,, Sample,,2,,, Sample,,3,,) 구하여 샘플의 평균값을 ( $ \overline{X_i} $ ) 살펴보고, 각 평균값의 차이가 (1) 모집단의 실제 값을 대표하는지와 (2) 이 평균값의 차이가 통계학적으로 의미가 있는지를 살펴 본다. 즉, 위의 그림에서 평균값 $\small\overline{X_1}$ , $\small\overline{X_2}$ , $\small\overline{X_3}$ 의 {2, 4, 6} 간의 차이를 가지고 연구자는 두 가지 종류의 해석을 할 수 있다.
첫 번째 해석은 $\small\text{H0: } \mu_1 = \mu_2 = \mu_3 $ 로 표현할 수 있다. 두 번째 표현은 수학표현으로 간단하게 나타내기 어려운 점이 있다. 연구자는 $\small\text{H1: } \mu_1 \not= \mu_2 \not= \mu_3 $ 의 경우만을 살펴 보려는 것이 아니라, $\small\text{H1: } \mu_1 \not= \mu_2 $ 의 경우나 $\small\text{H1: } \mu_2 = \mu_3$ 의 경우, $\small\text{H1: } \mu_1 \not= \mu_3 $ 의 경우 등을 모두 인정하고 있기 때문이다. 따라서 두 번째 해석은 다음과 같이 나타낼 수 있으며 이를 연구자의 연구가설로 한다.
1. 3 집단의 진짜 평균은 (모집단의 평균) 서로 다르지 않다. 3 샘플 집단 간의 차이는 순전히 우연만으로 나타난 것으로 이 차이를 가지고 전체 3 집단 간의 차이가 있다고 이야기 할 수 없다.
1. 3 샘플의 차이는 실제 모집단에서의 3 집단 간의 차이를 반영한다.
첫 번째 해석은 $\small\text{H0: } \mu_1 = \mu_2 = \mu_3 $ 로 표현할 수 있다. 두 번째 표현은 수학표현으로 간단하게 나타내기 어려운 점이 있다. 연구자는 $\small\text{H1: } \mu_1 \not= \mu_2 \not= \mu_3 $ 의 경우만을 살펴 보려는 것이 아니라, $\small\text{H1: } \mu_1 \not= \mu_2 $ 의 경우나 $\small\text{H1: } \mu_2 \not= \mu_3$ 의 경우, $\small\text{H1: } \mu_1 \not= \mu_3 $ 의 경우 등을 모두 인정하고 있기 때문이다. 따라서 두 번째 해석은 다음과 같이 나타낼 수 있으며 이를 연구자의 연구가설로 한다.
$\small\text{H1: }$ 적어도 한 집단의 평균이 다른 집단의 평균과 다를 것이다.
또한 첫 번째 해석은 위의 선언을 뒤집어 설명한 것으므로 [null hypothesis]([Hypothesis test] 참조)라고 하겠다.
또한 첫 번째 해석은 위의 선언을 뒤집어 설명한 것으므로 [wiki:NullHypothesis null hypothesis 혹은 영가설] ([Hypothesis test] 참조)라고 하겠다.
$\small\text{H0: } \mu_1 = \mu_2 = \mu_3 $
@@ -90,7 +98,7 @@
라고 표현할 수 있다. 그런데, [1] 식에서 만약에 처치효과가 (treatment effect) 없다면 F값이 어떻게 될까? treatment effect = 0 라고 한다면, F값의 계산에서 남는 것은 분모, 분자 모두 within group 내의 램덤 차이뿐이다. 여기서 일어나는 차이는 샘플링에 의해서 일어날 수 있는 약간의 차이라고 생각할 수 있으므로 분모와 분자의 값이 거의 일치하다고 가정을 할 수 있다. 이때의 F 값은 1이 된다. 즉, 예에서 보는 것처럼, 부모의 SES가 자녀의 과학성적에 영향을 주는가? 라는 질문에서 SES 효과가 없다면, 분산을 (variance) 구해서 분석한 (analysis) 결과 값은 1에 근접할 것이다.
식 [2]에서 언급한 것 처럼 F 값은 그룹 간의 차이와 (treatment difference) 그룹 내의 차이의 (error by chance) 비율을 구하는 것이다. 그렇다면 그룹간 차이와 (between group difference or variance), 그룹내 차이는 (within group difference or variance) 어떻게 구할까?
식 <2>에서 언급한 것 처럼 F 값은 그룹 간의 차이와 (treatment difference) 그룹 내의 차이의 (error by chance) 비율을 구하는 것이다. 그렇다면 그룹간 차이와 (between group difference or variance), 그룹내 차이는 (within group difference or variance) 어떻게 구할까?
== ANOVA 공식 ==세 개의 집단을 비교한다고 할 때, 우리가 구할 수 있는 분산 값은 세가지 종류가 있다. 즉 그림에서와 같이 세 그룹 간의 차이를 보는 분산이 있을 수 있으며, 각 그룹 내부의 구성원이 서로 얼마나 다른가를 보는 분산이 있을 수 있고, 그림에는 표시되어 있지 않지만 전체 구성원을 하나의 집단으로 놓고 보는 (즉, 그룹 간 구별을 하지 않는) 분산이 있다.
@@ -99,7 +107,7 @@
* 그룹 내 분산[[Attachment(anovaExample3.jpg,align=left,width="350",caption="ANOVA 3 group variance comparison")]]
전체 분산은 바로 그룹 간 분산과 그룹 내 분산을 모두 더한 값이 된다. 즉 Variance,,total,, = Variance,,between,, + Variance,,within,,. 이를 도식화해서 설명하자면,
전체 분산은 바로 그룹 간 분산과 그룹 내 분산을 모두 더한 값이 된다. 즉 Variation,,total,, = Variation,,between,, + Variation,,within,,. 이를 도식화해서 설명하자면,
|Variability Total|Between treatment variance ||Within treatment variance ||
||1. Treatment effect ||1. Differences due to chance ||
@@ -119,9 +127,9 @@
그리고, 앞서 이야기 한대로, 우리가 구하고자 하는 F 값은 between group difference를 within group difference로 나눈 값이므로:
$F = \displaystyle \frac{\displaystyle \frac{SS_{between}}{df_{between}}}{\displaystyle \frac{SS_{within}}{df_{within}}} = \frac{\text{Variance between group
$F = \frac{\displaystyle \frac{SS_{between}}{df_{between}}}{\displaystyle \frac{SS_{within}}{df_{within}}} = \displaystyle \frac{\text{Variance between group treatments}}{\text{Variance within group treatments}}$ 라고 할 수 있다. 그런데, F-test (ANOVA)를 만든 학자들은 Variance라는 용어 대신에 Mean Square ( $\text{MS}$ )라는 용어를 사용한다. [Variance]는 Sum of Square ( $\text{SS}$ )를 $\text{df}$ 로 나눈 것이니, Mean Square라고 부르는 것도 나름 합리적이다 (즉, $ \text{MS} = \text{Variance} = s^2 = \frac{SS}{df}$ ). 그리고 위의 F 값을
$ F = \displaystyle \frac {MS_{between}}{MS_{within}} $ 으로 정리한다.
아래의 예를 보자. 아래는 부모의 SES 수준에 따른 11살 어린이 자녀의 과학문제를 맞춘 갯수이다. 연구자는 SES라는 사회적 개념과 지적 능력이 어떤 연관이 있을까에서 시작하여, 이를 테스트 해보기 위해서 아래의 유사실험을 만들어 내었다.
@@ -138,23 +146,24 @@
|| {{{SS}}} || 6 || 4 || 6 || ||위의 표는 개인 점수 외에도 필요한 사항들을 가지고 있는데 이것 들에 대해서 우선 설명하겠다.
* T : 각각의 그룹 구성원의 점수 합을 (total) 의미한다.
* SS : Sum of Square 값을 의미한다. 표에서는 각 그룹(집단)의 SS 값이 구하여져 있다.
* n : 각 그룹 구성원의 숫자를 (이 경우에는 모두 5) 의미한다.
* G : 전체 합을 말한다. 즉, 세 그룹에 속한 모든 구성원의 점수 합을 G라고 하였다 (Grand total = 45).
* N : n과 대비하여 전체 구성원의 숫자를 말한다 (여기서는 5명씩 3그룹이 있으므로 15이다).
* k : 집단(그룹)의 숫자를 말한다. 여기서는 3 그룹이 있으므로 3이다.
* T : 각각의 그룹 구성원의 점수 합을 (total) 의미한다. {5, 10, 30}
* SS : Sum of Square 값을 의미한다. 표에서는 각 그룹(집단)의 SS 값이 구하여져 있다. {6, 4, 6}
* n : 각 그룹 구성원의 숫자를 (이 경우에는 모두 5) 의미한다. {5, 5, 5}
* G : 전체 합을 말한다. 즉, 세 그룹에 속한 모든 구성원의 점수 합을 G라고 하였다 (Grand total = 45). $ G = 45 $
* N : n과 대비하여 전체 구성원의 숫자를 말한다 (여기서는 5명씩 3그룹이 있으므로 15이다). $ N = 15 $
* k : 집단(그룹)의 숫자를 말한다. 여기서는 3 그룹이 있으므로 3이다. $ k = 3 $
* $\small\sum X^2$ : 이 값은 전체 분산값을 위해 미리 계산이 된 값이다. 전체 분산값을 구하기 위해서 이 값이 필요한 이유는 아래와 같다. \begin{eqnarray}
\text{SS} & = & \small{\sum} \normal (X_i-\overline{X})^2 \nonumber \\
& = & \small{\sum} \normal(X_i^2 - 2 \overline{X} X_i + \overline{X}^2 ) \nonumber \\
& = & \small{\sum} \normal X_i^2 - 2 \overline{X} \small{\sum} \normal X_i + \small{\sum} \normal \overline{X}^2 \nonumber\\
& = & \small{\sum} \normal X_i^2 - 2 n \overline{X}^2 + n \overline{X}^2 \;\cdots\; \text{cause } \small{\sum} \normal{X_i = n \overline{X} }; \nonumber\\
& = & \small{\sum} \normal X_i^2 - n \overline{X}^2 \;\cdots\; [1] \nonumber\\
& = & \small{\sum} \normal X_i^2 - \frac{(\small{\sum}\normal{X_i)^2}}{n} \;\cdots\; \text{cause } \overline{X}=\frac{\small\sum \normal X_i}{n} \;\; [2] \nonumber
\end{eqnarray}
{{{#!latex
\begin{eqnarray*}
\text{SS} & = & \sum (X_i-\overline{X})^2 \\
& = & \sum (X_i^2 - 2 \overline{X} X_i + \overline{X}^2 ) \\
& = & \sum X_i^2 - 2 \overline{X} \sum X_i + \sum \overline{X}^2 \\
& = & \sum X_i^2 - 2 n \overline{X}^2 + n \overline{X}^2 \;\cdots\; \text{cause } \sum {X_i = n \overline{X} }; \\
& = & \sum X_i^2 - n \overline{X}^2 \;\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\; [1] \\
& = & \sum X_i^2 - \frac{(\sum {X_i)^2}}{n} \;\cdots\cdots\cdots\; [2] \;\;\;\; \text{cause } \overline{X}=\frac{\sum X_i}{n} \;\;
\end{eqnarray*}
}}}== SS 분해 ==
@@ -170,10 +179,20 @@
}}} {{{#!latex
\begin{eqnarray}
\text{SS} & = & \sum X_i^2 - \frac{(\sum {X_i)^2}}{n} \nonumber\\
& = & 221 - \frac{(45)^2}{15} \nonumber\\
& = & 221 - 135 \nonumber\\
& = & 86 \nonumber
\end{eqnarray}
}}}
=== SS,,within,, === 두 번째로 알아봐야 할 것은 각각의 그룹 내에서 그룹 멤버들이 평균에서 얼마나 흩어져 있는가이다. 이 분산값은 이전에 소개된 분산값의 공식을 이용해서 구할 수 있다. 단, 여기서 비교하는 그룹이 세 개이므로 SS 값은 모두 3개를 구할 수 있으므로, SS,,within,, 값은 각각의 그룹 분산을 모두 더한 값이다.
{{{#!latex
SS_{within}} = \sum {SS_{each group}
}}}
위에서 각각의 SS값은 미리 구해 두었으므로, 이를 계산하면,
{{{#!latex
@@ -217,21 +236,24 @@
SS값이 분해되어서 나누어지는 과정을 도식화 해보면 다음과 같다. attachment:ANOVA_ssAnalysis.png
== df 분해 ==
df (degrees of freedom) 역시 SS와 같은 방식을 취한다. 즉 df,,total,,= df,,between,,+df,,within,,으로 표현될 수 있다. 따라서, 각각의 조건에 맞는 df를 구해야 한다. 일반적으로 df값은 전체 (샘플) 구성원에서 1을 뺀 값을 갖는다. 예를 들면 $\small S^2=\frac{SS}{df}$ 에서 df는 바로 샘플 숫자 n에서 1을 뺀 n-1이다.
$df$ ([wiki:DegreesOfFreedom degrees of freedom]) 역시 SS와 같은 방식을 취한다. 즉 $ df_{total} = df_{between} + df_{within} $ 으로 표현될 수 있다. 따라서, 각각의 조건에 맞는 $df$ 를 구해야 한다. 일반적으로 $df$ 값은 전체 (샘플) 구성원에서 1을 뺀 값을 갖는다. 예를 들면 $ S^2=\frac{SS}{df} $ 에서 $df$ 는 바로 샘플 숫자 n에서 1을 뺀 n-1이다.
__Total degrees of freedom__ $ df_{total} $
$ df_{total} $ 값은 그룹 소속을 막론한 전체 샘플 구성원의 숫자에서 1을 뺀 값이다. 즉, $df_{total}= N -1$
따라서 위 예의 $ df_{total} $ 값은
\begin{eqnarray}
df_{total} & = & 15 - 1 \nonumber \\
& = & 14 \nonumber
\end{eqnarray}
\begin{eqnarray*}
df_{total} & = & 15 - 1 \\
& = & 14
\end{eqnarray*}
}}} df,,within,,:
__Within degrees of freedom__ $ df_{within} $
$df_{within}=\small\sum\large(n_i-1)$
@@ -250,24 +272,26 @@
}}}__Between degrees of freedom__ $ df_{between} $
그룹 간 분산에 사용되어야 하는 df값은 전체 그룹 숫자에서 1을 뺀 값이다. 즉,
위의 예를 적용해 보면
$df_{between} = k -1 $
위의 예를 적용해 보면
\begin{eqnarray}
df_{between} & = & 3 - 1 \nonumber \\
& = & 2 \nonumber
\end{eqnarray}
{{{#!latex
\begin{eqnarray*}
df_{between} & = & 3 - 1 \\
& = & 2
\end{eqnarray*}
}}}SS 분석에서도 살펴 보았듯이 df에서도 df,,total,,= df,,between,, + df,,within,, 의 형태를 갖는
다.
attachment:ANOVA_dfAnalysis.png
attachment:ANOVA_dfAnalysis.png
== 분산 값과 (MS) F 값 구하기 ==
위에서 구한 값들을 요약 정리해보면 아래의 테이블과 같다.
@@ -282,7 +306,7 @@
$\displaystyle variance = \frac{SS}{n-1} = \frac{SS}{df} $
ANOVA에서는 위의 variance라는 용어를 MS라고 부르는게 관습이다 (Mean Square). 용어를 들어보면 Sum of Square값을 n-1로 나누었다고 하여 만들어진 듯 하다. 따라서,
ANOVA에서는 위의 variance라는 용어를 MS라고 부르는게 관습이라고 하였다.
$\displaystyle MS = \frac{SS}{df}$
@@ -303,7 +327,7 @@
$\displaystyle F=\frac{35}{1.33} = 26.25$우리가 구한 26.25 값이 의미하는 것은 F 값의 분모와 분자 중 분자의 값이 분모의 값보다 상당히 크다는 것이다. F 값이나 t 값이나 구하는 공식의 공통적인 논리는 연구자가 발견하는 차이가 (obtained difference) 연구자가 어쩔 수 없이 만나게 되는 차이의 (difference by chance) 비율이 일정 숫자를 넘어서면 그룹 간의 차이를 인정하는 것이었다. 따라서, 위에서 구한 F-ratio 값은 우연히 나올 수 있는 variance의 차이가 (MS,,within,,), 그룹 간 실제 차이의 (MS,,between,,) 20배가 넘는다는 것을 의미하니, 그룹 차이가 있다고 판단하는 것이 옳을 것이다. 그러나, 이와 같은 판단을 내리기 위해서는 F distribution table을 살펴 보아야 한다.
우리가 구한 26.25 값이 의미하는 것은 F 값의 분모와 분자 중 분자의 값이 분모의 값보다 상당히 크다는 것이다. F 값이나 t 값이나 구하는 공식의 공통적인 논리는 연구자가 발견하는 차이가 (obtained difference) 연구자가 어쩔 수 없이 만나게 되는 차이의 (difference by chance) 비율이 일정 숫자를 넘어서면 그룹 간의 차이를 인정하는 것이었다. 따라서, 위에서 구한 F-ratio 값은 우연히 나올 수 있는 variance의 차이가 (MS,,within,,), 그룹 간 실제 차이의 (MS,,between,,) 20배가 넘는다는 것을 의미하니, 그룹 차이가 있다고 판단하는 것이 옳을 것이다. 그러나, 이와 같은 판단을 내리기 위해서는 F distribution table을 살펴 보아야 한다. http://commres.net/wiki/_media/ftable.pdf 참조
||<table class="wikiLeft">|||||||||| '''ANOVA''' ||
||Science Knowledge || || || || || ||
@@ -346,7 +370,7 @@
= 논문 작성 =
{{|
||||||||||<table class="wikiRight"> Table 1. Amount of time (days) the pain relieved ||
||||||||||<table class="wikiCenter"> Table 1. Amount of time (days) the pain relieved ||
|| -- || Placebo || Drug A || Drug B || Drug C |||| M || 1.0 || 1.0 || 4.0 || 6.0 ||
|| SD || 1.73 || 1.0 || 1.0 || 1.73 ||
@@ -380,6 +404,33 @@
$F = t^2$
= Example =
|| ||First Letter Condition 1 [[br]]X,,1,, ||Last Letter Condition 2 [[br]]X,,2,, ||No Letter Condition 3 [[br]]X,,3,, ||
|| || 15 || 21 || 28 ||
|| || 20 || 25 || 30 ||
|| || 14 || 29 || 32 ||
|| || 13 || 18 || 28 ||
|| || 18 || 26 || 26 ||
|| || 16 || 22 || 30 ||
|| || 13 || 26 || 25 ||
|| || 12 || 24 || 36 ||
|| || 18 || 28 || 20 ||
|| || 11 || 21 || 25 ||
||Mean ||$\overline{X_1}$ = 15 ||$\overline{X_2}$ = 24 ||$\overline{X_3}$ = 28 ||
||Total ||$ T_1 = 150 $ ||$ T_2 = 240 $ ||$ T_3 = 280 $ ||
||Squared Total ||$ T_1^2 = 22500 $ ||$ T_2^2 = 57600 $ ||$ T_3^2 = 78400 $ ||
$ G = ? $
$ G^2 = ? $
$ \sum {X^2} = ? $
$ k = $
$ n = $
$ N = $
$ df_{total} = $
$ df_{between} = $
$ df_{within} = $
= Factorial design =[wiki:FactorialAnova Factorial Anova] Two factor ANOVA with independent measure
= ANOVA (__AN__alysis __O__f __VA__riance) =
See also FactorialAnova
Contents
1. ANOVA (ANalysis Of VAriance), F-test ¶
...
T-test 사용은 기본적으로 두 가지면에서 한계를 갖는다. 첫째는 독립변인으로 오로지 2 그룹만을 비교할 수 없다는 것이다. (예를 들 것). 두번째로는 t test 는 오직 하나만의 독립변인을 검증한다는 것이다. (예를 들 것).
T-test 사용은 기본적으로 두 가지면에서 한계를 갖는다. 첫째는 독립변인으로 오로지 2 그룹만을 비교할 수 없다는 것이다. (예를 들 것). 두번째로는 t test 는 오직 하나만의 독립변인을 검증한다는 것이다. (예를 들 것).
ANOVA는 2개 이상의 treatment 혹은 population 집단의 평균 점수를 평가하는데 쓰이는 가설 검증 절차이다. 추정통계가 (Inferential statistics) 모두 그렇듯이, ANOVA 또한 샘플의 평균값으로 모집단의 평균값을 추정하여 각 집단 간의 차이가 통계학적으로 의미가 있는지 살펴보는 절차이다. ANOVA와 T-test는 샘플 그룹 간의 평균을 비교한다는 의미에서 서로 비슷하게 보이지만, ANOVA는 T-test에 비해 월등한 이점을 가지고 있다. 특히 T-test의 경우에는 두 집단 간의 비교만 가능하지만, ANOVA는 두개 혹은 그 이상의 집단 간의 평균을 비교하는것이 가능하다. 따라서 연구자는 ANOVA를 이용하여 실험이나 서베이 등을 좀 더 유연하게 디자인할 수 있다.
| ANOVA | |||
| 4 학년 | 5 학년 | 6 학년 | |
| 샘플 1의 과학 지식 점수 | 샘플 2의 과학 지식 점수 | 샘플 3의 과학 지식 점수 | |
| * 독립변인: 학년 * 종속변인: 과학지식 | |||
T-test와 마찬가지로, ANOVA 또한 독립적인 측정으로 이루어진 집단의 비교나 (Independent T-test) 반복 측정 (repeated measure)으로 나타나는 동일 집단의 시간차 비교에 사용될 수 있다. 독립적인 측정이라 함은 2개 이상의 treatment(처치 혹은 실험처치)나 2개 이상의 모집단에서 (예, 남자와 여자) 나타나는 상호배타적인 집단을 비교하는 것을 말한다.
반면에 반복측정은 여러가지 (두 번 이상의) 처치를 한 그룹이 시간을 두고 측정을 받는 것을 의미한다. 예를 들면, 5학년 아동들을 대상으로 미디어교육을 받기 전에 게임에 사용하는 시간을 측정을 하고, 같은 그룹을 미디어교육을 받은 후에 다시 측정 하는 것을 "반복측정"이라고 한다.
| Factorial design | |||||
| 독립변인: 학생 수 | |||||
| Small | Medium | Large | |||
| 독립변인2: 교육방법 | A방법 | 샘플1 | 샘플2 | 샘플3 | |
| B방법 | 샘플4 | 샘프5 | 샘플6 | ||
| * 두 개의 독립변인: 학생 수와 교육방법 * 하나의 종속변인: 과학지식 | |||||
ANOVA는 또한 두 가지 이상의 독립변인의 (Independent variable (VariablesIdentification 참조)) 효과를 동시에 살펴보는데 사용되기도 한다. 가령, 연구자는 ANOVA를 이용하여 사용자 유저인터페이스의 종류와 (A, B, C: Independent Variable 1) 동영상의 사용 (있고 없음, Independent Variable 2)가 과학지식의 습득에 얼마나 영향을 주는지 동시에 살펴볼 수 있다.
2. Factors ¶
위의 표에서 사용된 용어인 독립변인을 (attributes) ANOVA에서는 팩터라고 (factor) 부른다. 위의 첫 번째 표에서 처럼 하나의 독립변인이 (factor) 이용된 경우 single factor design 이라고 하며, 두 번째처럼 두 개 이상의 독립변인이 이용된 경우를 factorial design 이라고 부른다 (FactorialAnova 참조).
3. Single Factor Design ¶
아래의 그림은 부모의 사회경제적 지위에 따른 과학점수의 차이를 보여주는 예이다. Group1(H), Group2(M), Group3(L)의 세집단의 그룹 멤버쉽에 따라서 과학점수 ( 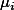 )의 평균이 다를 것이라는 것이 연구자의 관심사이다.
)의 평균이 다를 것이라는 것이 연구자의 관심사이다.
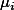 )의 평균이 다를 것이라는 것이 연구자의 관심사이다.
)의 평균이 다를 것이라는 것이 연구자의 관심사이다.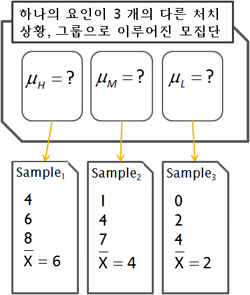
three group comparison [PNG image (25.73 KB)]
위의 그림에서 연구자는 전체 모집단에서 3가지의 특성을 (attributes) 가지는 하위 집단을 규정하고, 이 집단의 특성이 서로 다른가에 대한 의문을 갖는 것을 나타낸다 (그림의 위쪽 부분). 연구자는 이 상태에서 각 집단의 구성원을 모두 조사할 수는 없으므로, 각각의 특성에 일치하는 샘플을 (Sample1, Sample2, Sample3) 구하여 샘플의 평균값을 ( 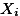 ) 살펴보고, 각 평균값의 차이가 (1) 모집단의 실제 값을 대표하는지와 (2) 이 평균값의 차이가 통계학적으로 의미가 있는지를 살펴 본다. 즉, 위의 그림에서 평균값
) 살펴보고, 각 평균값의 차이가 (1) 모집단의 실제 값을 대표하는지와 (2) 이 평균값의 차이가 통계학적으로 의미가 있는지를 살펴 본다. 즉, 위의 그림에서 평균값 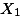 ,
, 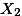 ,
, 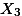 의 {2, 4, 6} 간의 차이를 가지고 연구자는 두 가지 종류의 해석을 할 수 있다.
의 {2, 4, 6} 간의 차이를 가지고 연구자는 두 가지 종류의 해석을 할 수 있다.
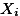 ) 살펴보고, 각 평균값의 차이가 (1) 모집단의 실제 값을 대표하는지와 (2) 이 평균값의 차이가 통계학적으로 의미가 있는지를 살펴 본다. 즉, 위의 그림에서 평균값
) 살펴보고, 각 평균값의 차이가 (1) 모집단의 실제 값을 대표하는지와 (2) 이 평균값의 차이가 통계학적으로 의미가 있는지를 살펴 본다. 즉, 위의 그림에서 평균값 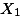 ,
, 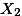 ,
, 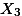 의 {2, 4, 6} 간의 차이를 가지고 연구자는 두 가지 종류의 해석을 할 수 있다.
의 {2, 4, 6} 간의 차이를 가지고 연구자는 두 가지 종류의 해석을 할 수 있다.- 3 집단의 진짜 평균은 (모집단의 평균) 서로 다르지 않다. 3 샘플 집단 간의 차이는 순전히 우연만으로 나타난 것으로 이 차이를 가지고 전체 3 집단 간의 차이가 있다고 이야기 할 수 없다.
- 3 샘플의 차이는 실제 모집단에서의 3 집단 간의 차이를 반영한다.
 로 표현할 수 있다. 두 번째 표현은 수학표현으로 간단하게 나타내기 어려운 점이 있다. 연구자는
로 표현할 수 있다. 두 번째 표현은 수학표현으로 간단하게 나타내기 어려운 점이 있다. 연구자는 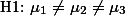 의 경우만을 살펴 보려는 것이 아니라,
의 경우만을 살펴 보려는 것이 아니라, 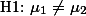 의 경우나
의 경우나 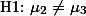 의 경우,
의 경우, 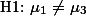 의 경우 등을 모두 인정하고 있기 때문이다. 따라서 두 번째 해석은 다음과 같이 나타낼 수 있으며 이를 연구자의 연구가설로 한다.
의 경우 등을 모두 인정하고 있기 때문이다. 따라서 두 번째 해석은 다음과 같이 나타낼 수 있으며 이를 연구자의 연구가설로 한다. 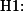 적어도 한 집단의 평균이 다른 집단의 평균과 다를 것이다.
적어도 한 집단의 평균이 다른 집단의 평균과 다를 것이다. 
- 그룹 혹은 집단의 숫자가 늘어나게 되면 해야 할 t-test가 급격하게 늘어나게 된다. 3집단일 경우에는 3번에 그치지만, 4집단일 경우는 6번으로 늘어나게 된다. 즉,
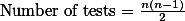 의 테스트가 필요하게 된다.
의 테스트가 필요하게 된다.
- 한 번의 t-test를 할 때마다, TypeIError의 양이 늘어나게 된다.
3.1. Logic ¶
위의 그림에서 연구자가 가지는 관심은 세집단 (Group1, Group2, Group3) 간의 차이이다. 이 차이가 일어나게 되는 이유는 두 가지가 있을 수 있다.
- 세 집단으로 구분되는 특성에 따른 차이가 있다. 즉, 독립 변인이라고 할 수 잇는 사회경제적지위 (SES)가 상, 중, 하 (Hi, Medium, Lo)로 나누어질 수 있는데, 이 특성이 영향력을 미쳐서 자녀의 과학점수 차이가 나타난다.
- 연구자가 피할 수 없는 개인 간의 차이에 의한 차이가 있다. 즉, 설령 세그룹 간의 특성으로 인해서 나타나는 차이를 제외하더라도, 순수한 개인 간 차이에서 기인하는 차이가 있을 수 있다.
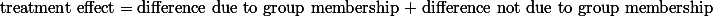
연구자의 독립변인의 특성의 영향력 간의 차이를 비교한다고 하면 위의 예처럼 바로 treatment effect의 크기를 집단 간에 비교해 보는 것이다.
연구자는 또한 Treatment effect를 비교하는 것과 함께, 동일 그룹 내의 차이를 비교해 볼 수도 있다. 동일 그룹 내 구성원 간의 차이란 똑같은 상황에서 나타나는 차이를 말한다. 부모의 SES가 "상(H)"이라고 할 때, 이 샘플 그룹 내 구성원 간의 차이 또한 나타날 것이다. 그런데, 이 경우 구성원의 과학점수는 동일한 조건에서 측정되므로 이 때 나타나는 차이는 순전히 Random한 차이라고 할 수 있다. 이를 그룹내 효과 (Within group effect)라고 한다.
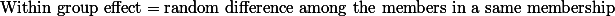
결국, Analysis of Variance라 함은 세 그룹 간의 평균이 얼마나 서로 멀리 떨어져 있는가 (treatment effect)를 살펴 보고, 이 차이가 충분한가를 판단하는 작업이라고 하겠다. 여기서 t-test의 개념적 논리를 다시 살펴보면 다음과 같다.
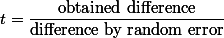
Obtained difference라 함은, 연구자가 두 그룹 간의 평균을 실제로 구해서(obtained) 그 차이를 (difference) 살펴 본 것을 말한다. 또한, difference by random error라 함은 두 그룹 간의 차이가 실제로는 없다고 하여도, 샘플링을 하기 때문에 나타날 수 밖에 없은, 연구자가 어쩔 수 없는 차이라고 하겠다.
ANOVA 또한 이 논리를 따른다 (즉, t-test의 논리를 Variance를 사용하여 구하는 것이다).
![$F = \displaystyle \frac{\text{difference (variance) obtained (due to membership) + difference (variance) by error}}{\text{difference (variance) by error}}\;\cdots\cdots\;[1]$ $F = \displaystyle \frac{\text{difference (variance) obtained (due to membership) + difference (variance) by error}}{\text{difference (variance) by error}}\;\cdots\cdots\;[1]$](/_cache/latex/c/ca/17e90c517e424f68531c6af93eff32b1.png)
위의 F-test에서 분자의 부분을 살펴 보면, 이는 treatment로 인해서 나타나는 차이를 말한다. 즉, 각각의 그룹의 상태가 다른 조건이었기 때문에 일어나는 차이를 말하므로, 그룹 간의 차이(between group difference)라고 이야기 할 수 있다. 반면에 분모 부분은 동일한 조건(within group)에서 연구자가 어쩔 수 없이 만나게 되는 차이를 말한다. 이를 그룹내 차이(within group difference)라고 한다. 따라서 위의 F-test는:
![\begin{eqnarray}
F = \frac{\text{treatment difference}}{\text{random difference}}
= \frac{\text{between group difference (variance)}}{\text{within group difference}} \;\cdots\cdots\; [2] \nonumber
\end{eqnarray}
\begin{eqnarray}
F = \frac{\text{treatment difference}}{\text{random difference}}
= \frac{\text{between group difference (variance)}}{\text{within group difference}} \;\cdots\cdots\; [2] \nonumber
\end{eqnarray}](/_cache/latex/d/d1/9e3e7ce059ce36c8e522463900e1eab3.png)
라고 표현할 수 있다. 그런데, 1 식에서 만약에 처치효과가 (treatment effect) 없다면 F값이 어떻게 될까? treatment effect = 0 라고 한다면, F값의 계산에서 남는 것은 분모, 분자 모두 within group 내의 램덤 차이뿐이다. 여기서 일어나는 차이는 샘플링에 의해서 일어날 수 있는 약간의 차이라고 생각할 수 있으므로 분모와 분자의 값이 거의 일치하다고 가정을 할 수 있다. 이때의 F 값은 1이 된다. 즉, 예에서 보는 것처럼, 부모의 SES가 자녀의 과학성적에 영향을 주는가? 라는 질문에서 SES 효과가 없다면, 분산을 (variance) 구해서 분석한 (analysis) 결과 값은 1에 근접할 것이다.
식 <2>에서 언급한 것 처럼 F 값은 그룹 간의 차이와 (treatment difference) 그룹 내의 차이의 (error by chance) 비율을 구하는 것이다. 그렇다면 그룹간 차이와 (between group difference or variance), 그룹내 차이는 (within group difference or variance) 어떻게 구할까?
3.2. ANOVA 공식 ¶
세 개의 집단을 비교한다고 할 때, 우리가 구할 수 있는 분산 값은 세가지 종류가 있다. 즉 그림에서와 같이 세 그룹 간의 차이를 보는 분산이 있을 수 있으며, 각 그룹 내부의 구성원이 서로 얼마나 다른가를 보는 분산이 있을 수 있고, 그림에는 표시되어 있지 않지만 전체 구성원을 하나의 집단으로 놓고 보는 (즉, 그룹 간 구별을 하지 않는) 분산이 있다.
- 전체 분산
- 그룹 간 분산
- 그룹 내 분산
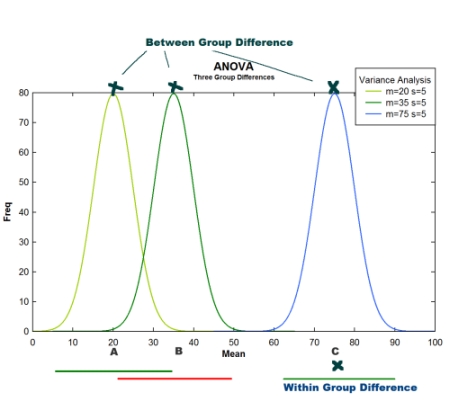
ANOVA 3 group variance comparison [JPG image (51.19 KB)]
전체 분산은 바로 그룹 간 분산과 그룹 내 분산을 모두 더한 값이 된다. 즉 Variationtotal = Variationbetween + Variationwithin. 이를 도식화해서 설명하자면,
| Between treatment variance | Within treatment variance |
| 1. Treatment effect | 1. Differences due to chance |
| 2. Differences due to chance |
라고 할 수 있다.
참고로 분산을 구하는 방법은:
![$s^2 = \frac{SS}{df}\;\cdots\;[3]$ $s^2 = \frac{SS}{df}\;\cdots\;[3]$](/_cache/latex/1/1d/10ecfb2d6795e495efc1693e926cc851.png)
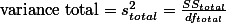

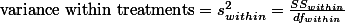
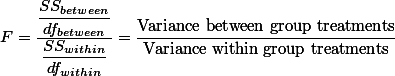 라고 할 수 있다. 그런데, F-test (ANOVA)를 만든 학자들은 Variance라는 용어 대신에 Mean Square (
라고 할 수 있다. 그런데, F-test (ANOVA)를 만든 학자들은 Variance라는 용어 대신에 Mean Square ( 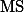 )라는 용어를 사용한다. Variance는 Sum of Square (
)라는 용어를 사용한다. Variance는 Sum of Square (  )를
)를 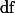 로 나눈 것이니, Mean Square라고 부르는 것도 나름 합리적이다 (즉,
로 나눈 것이니, Mean Square라고 부르는 것도 나름 합리적이다 (즉, 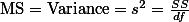 ). 그리고 위의 F 값을
). 그리고 위의 F 값을 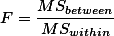 으로 정리한다.
으로 정리한다.| SES condition | ||||
| Group 1 (L) | Group 2 (M) | Group 3 (H) | ||
| 0 | 1 | 7 | 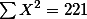 G = 45 N = 15 k = 3 | |
| 1 | 2 | 6 | ||
| 3 | 3 | 4 | ||
| 1 | 3 | 6 | ||
| 0 | 1 | 7 | ||
| T | 5 | 10 | 30 | |
| n | 5 | 5 | 5 | |
 | 1 | 2 | 6 | |
| SS | 6 | 4 | 6 | |
위의 표는 개인 점수 외에도 필요한 사항들을 가지고 있는데 이것 들에 대해서 우선 설명하겠다.
- T : 각각의 그룹 구성원의 점수 합을 (total) 의미한다. {5, 10, 30}
- SS : Sum of Square 값을 의미한다. 표에서는 각 그룹(집단)의 SS 값이 구하여져 있다. {6, 4, 6}
- n : 각 그룹 구성원의 숫자를 (이 경우에는 모두 5) 의미한다. {5, 5, 5}
- G : 전체 합을 말한다. 즉, 세 그룹에 속한 모든 구성원의 점수 합을 G라고 하였다 (Grand total = 45).

- N : n과 대비하여 전체 구성원의 숫자를 말한다 (여기서는 5명씩 3그룹이 있으므로 15이다).

- k : 집단(그룹)의 숫자를 말한다. 여기서는 3 그룹이 있으므로 3이다.

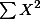 : 이 값은 전체 분산값을 위해 미리 계산이 된 값이다. 전체 분산값을 구하기 위해서 이 값이 필요한 이유는 아래와 같다.
: 이 값은 전체 분산값을 위해 미리 계산이 된 값이다. 전체 분산값을 구하기 위해서 이 값이 필요한 이유는 아래와 같다.
![\begin{eqnarray*}
\text{SS} & = & \sum (X_i-\overline{X})^2 \\
& = & \sum (X_i^2 - 2 \overline{X} X_i + \overline{X}^2 ) \\
& = & \sum X_i^2 - 2 \overline{X} \sum X_i + \sum \overline{X}^2 \\
& = & \sum X_i^2 - 2 n \overline{X}^2 + n \overline{X}^2 \;\cdots\; \text{cause } \sum {X_i = n \overline{X} }; \\
& = & \sum X_i^2 - n \overline{X}^2 \;\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\; [1] \\
& = & \sum X_i^2 - \frac{(\sum {X_i)^2}}{n} \;\cdots\cdots\cdots\; [2] \;\;\;\; \text{cause } \overline{X}=\frac{\sum X_i}{n} \;\;
\end{eqnarray*}
\begin{eqnarray*}
\text{SS} & = & \sum (X_i-\overline{X})^2 \\
& = & \sum (X_i^2 - 2 \overline{X} X_i + \overline{X}^2 ) \\
& = & \sum X_i^2 - 2 \overline{X} \sum X_i + \sum \overline{X}^2 \\
& = & \sum X_i^2 - 2 n \overline{X}^2 + n \overline{X}^2 \;\cdots\; \text{cause } \sum {X_i = n \overline{X} }; \\
& = & \sum X_i^2 - n \overline{X}^2 \;\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\; [1] \\
& = & \sum X_i^2 - \frac{(\sum {X_i)^2}}{n} \;\cdots\cdots\cdots\; [2] \;\;\;\; \text{cause } \overline{X}=\frac{\sum X_i}{n} \;\;
\end{eqnarray*}](/_cache/latex/7/75/7a3ee84bd58b4c562f19cb67d1123a0f.png)
3.3.2. SSwithin ¶
두 번째로 알아봐야 할 것은 각각의 그룹 내에서 그룹 멤버들이 평균에서 얼마나 흩어져 있는가이다. 이 분산값은 이전에 소개된 분산값의 공식을 이용해서 구할 수 있다. 단, 여기서 비교하는 그룹이 세 개이므로 SS 값은 모두 3개를 구할 수 있으므로, SSwithin 값은 각각의 그룹 분산을 모두 더한 값이다.
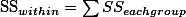
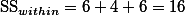
3.3.3. SSbetween ¶
앞서 언급 하였듯이 그룹 간의(bewteen group) SS값은 SStotal 값에서 SSwithin 값을 제외한 값이 된다. SStotal = 85 이었고, SSwithin = 16 이었으므로,
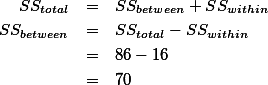
이라고 할 수 있다. 실제 SSbetween값을 구하는 공식을 사용하여 구해보면 아래와 같다.
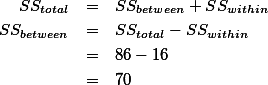
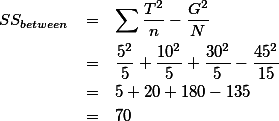
혹은 SSbetween 값을 구하는 방식을 도출해 보면 다음과 같다. 그룹 간의 (between group) 분산을 구한다는 것은 세 평균이 전체 평균에서 얼마나 각각 떨어져 있는가를 보는 것이므로
이라고 할 수 있는데,
의 합은 전체평균에서 그룹 평균을 뺀 값의 합으로 정확히 그룹의 분산을 위한 값이라고 할 수는 없다. 오히려 각각의 값에 그룹 구성원의 숫자를 곱해주는 것이 그룹들의 분산 값을 보여 주는 지표라고 할 수 있다. 따라서,
SS값이 분해되어서 나누어지는 과정을 도식화 해보면 다음과 같다.
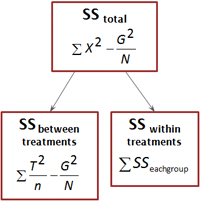

[PNG image (13.07 KB)]
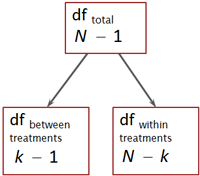
3.4. df 분해 ¶
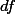 (degrees of freedom) 역시 SS와 같은 방식을 취한다. 즉
(degrees of freedom) 역시 SS와 같은 방식을 취한다. 즉 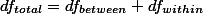 으로 표현될 수 있다. 따라서, 각각의 조건에 맞는
으로 표현될 수 있다. 따라서, 각각의 조건에 맞는 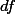 를 구해야 한다. 일반적으로
를 구해야 한다. 일반적으로 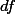 값은 전체 (샘플) 구성원에서 1을 뺀 값을 갖는다. 예를 들면
값은 전체 (샘플) 구성원에서 1을 뺀 값을 갖는다. 예를 들면  에서
에서 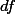 는 바로 샘플 숫자 n에서 1을 뺀 n-1이다.
는 바로 샘플 숫자 n에서 1을 뺀 n-1이다. Total degrees of freedom 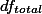
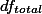
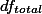 값은 그룹 소속을 막론한 전체 샘플 구성원의 숫자에서 1을 뺀 값이다. 즉,
값은 그룹 소속을 막론한 전체 샘플 구성원의 숫자에서 1을 뺀 값이다. 즉, 
따라서 위 예의
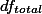 값은
값은
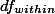
그룹 내의 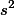 값을 구할 때 사용하는 n-1, 즉 각각의 그룹의 분산에서 사용되는 n1-1; n2-1; n3-1 의 값을 모두 더하여 dfwithin을 구한다. 즉,
값을 구할 때 사용하는 n-1, 즉 각각의 그룹의 분산에서 사용되는 n1-1; n2-1; n3-1 의 값을 모두 더하여 dfwithin을 구한다. 즉,
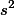 값을 구할 때 사용하는 n-1, 즉 각각의 그룹의 분산에서 사용되는 n1-1; n2-1; n3-1 의 값을 모두 더하여 dfwithin을 구한다. 즉,
값을 구할 때 사용하는 n-1, 즉 각각의 그룹의 분산에서 사용되는 n1-1; n2-1; n3-1 의 값을 모두 더하여 dfwithin을 구한다. 즉,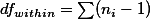
다른 방법으로는 그룹 구성을 무시한 전체 샘플 숫자, N에서 그룹 숫자를 (여기서는 k = 3) 빼서 구할 수 있다. 이 편이 더하는 수고를 덜으므로 편리하다 하겠다.
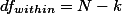
따라서 예에서 구해야 하는 dfwithin 값은:

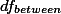
그룹 간 분산에 사용되어야 하는 df값은 전체 그룹 숫자에서 1을 뺀 값이다. 즉,
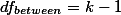
위의 예를 적용해 보면
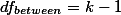
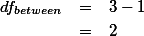
다.
[PNG image (10.71 KB)]
3.5. 분산 값과 (MS) F 값 구하기 ¶
위에서 구한 값들을 요약 정리해보면 아래의 테이블과 같다.
| 각각의 SS와 df값 | |
| SStotal = 86 | dftotal = 14 |
| SSwithin = 17 | dfwithin = 12 |
| SSbetween = 70 | dfbetween = 2 |
누누이 언급된 것이지만 variance값은 아래와 같이 구한다.
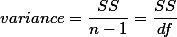
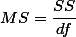
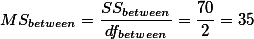
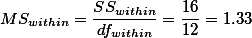
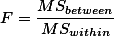
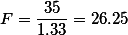
| ANOVA | |||||
| Science Knowledge | |||||
| Sum of Squares | df | Mean Square | F | Sig. | |
| Between Groups | 70 | 2 | 35 | 26.25 | 0.000 |
| Within Groups | 16 | 12 | 1.333 | ||
| Total | 86 | 14 | |||
4. 샘플 숫자가 Treatment마다 다를때 ¶
| Experiment | |||
| Vervet | Rhesus | Baboon | |
| n = 4 | n = 10 | n = 6 | N = 20 |
 = 9 = 9 |  = 14 = 14 |  = 4 = 4 | G = 200 |
| T = 36 | T = 140 | T = 24 | 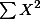 = 3400 = 3400 |
| SS = 200 | SS = 500 | SS = 320 | |
숫자가 다른 샘플을 비교할 때도 마찬가지로 계산한다.
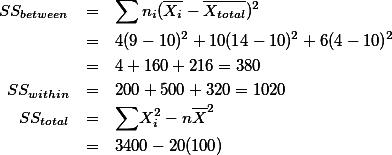
dfbetween = k - 1 = 2
dfwithin = (4-1) + (10-1) + (6-1)
dftotal = N -1 = 20 -1 = 19
F = 3.17
5. 논문 작성 ¶
| Table 1. Amount of time (days) the pain relieved | ||||
| -- | Placebo | Drug A | Drug B | Drug C |
| M | 1.0 | 1.0 | 4.0 | 6.0 |
| SD | 1.73 | 1.0 | 1.0 | 1.73 |
위에서 F-ratio가 제시되는 형식을 익혀 두어야 한다. 괄호 안의 두 숫자는 between, within df값을 의미한다. 다음으로 등호와 함께 계산된 F값을 보고해야 한다. 이 값이 어느 정도의 오류가능성을 갖는가에 대한 평가를 (즉, TypeIError) 기록해야 한다. 위에서 주의해야 할 점은 F값에 대한 판단은 4개의 집단 중 어디에서 차이가 발생했는지 (A-B? B-C? Placebo-C?)를 제시해 주지 않는다는 것이다. 따라서, 어떤 처치(treatment) 간에 통계학적으로 유의미한 차이가 보이는가는 post-hoc 테스트를 통해서 밝혀야 한다 (SheffeeTest).
| ANOVA Summary | ||||
| Source | SS | df | MS | |
| Between treatments | 54 | 3 | 18 | F = 9.0 * |
| Within treatments | 16 | 8 | 2 | |
| Total | 70 | 11 | ||
6. 개념 이해 ¶
아래는 두 실험의 결과를 기록한 표이다 (각각 case 1과 case 2로 표시). ANOVA를 개념적으로 이해했다면 각각의 ANOVA 값의 크기가 어느 정도인지 예측할 수 있어야 한다.
| Case 1 | -- | Case 2 | |||
| I | II | -- | I | II | |
| 29 | 34 | -- | 16 | 28 | |
| 30 | 35 | -- | 30 | 31 | |
| 30 | 35 | -- | 36 | 35 | |
| 31 | 36 | -- | 38 | 46 | |
 = 30 = 30 |  = 35 = 35 | -- |  = 30 = 30 |  = 35 = 35 | |
| SS = 2 | SS = 2 | -- | SS = 296 | SS = 186 | |
9. Example ¶
| First Letter Condition 1 X1 | Last Letter Condition 2 X2 | No Letter Condition 3 X3 | |
| 15 | 21 | 28 | |
| 20 | 25 | 30 | |
| 14 | 29 | 32 | |
| 13 | 18 | 28 | |
| 18 | 26 | 26 | |
| 16 | 22 | 30 | |
| 13 | 26 | 25 | |
| 12 | 24 | 36 | |
| 18 | 28 | 20 | |
| 11 | 21 | 25 | |
| Mean | 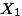 = 15 = 15 | 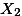 = 24 = 24 | 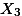 = 28 = 28 |
| Total |  |  |  |
| Squared Total | 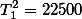 | 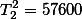 | 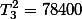 |

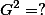
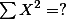
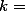

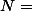
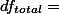
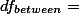
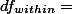
10. Factorial design ¶
Factorial Anova Two factor ANOVA with independent measure
11. ANOVA (ANalysis Of VAriance) ¶
Let's talk about ANOVA. Unlike its monstrous name -- sounds like one of zombie kinds, it is somewhat simple. That is, ANOVA is analysis of variance. If you know what variance is and understand some important issues in the t-test, which we previously discussed, it should be simple to understand.
Before going further, I need some clarification of terms. Suppose we have three groups to compare their exam scores. Each group has 20 members. Then, when we say compare between groups, we mean we see each group as a unit and compare the three groups. So, we are talking about the three groups, not the individual members of the three groups. On the other hand, when we say compare (members) within group, we mean we compare the members of each group. We set one group (out of the three groups) aside, and compare each individual to each other within the group.
Before going further, I need some clarification of terms. Suppose we have three groups to compare their exam scores. Each group has 20 members. Then, when we say compare between groups, we mean we see each group as a unit and compare the three groups. So, we are talking about the three groups, not the individual members of the three groups. On the other hand, when we say compare (members) within group, we mean we compare the members of each group. We set one group (out of the three groups) aside, and compare each individual to each other within the group.
It is always better to attack the basics when we run into complicated problem (the monster, ANOVA). So, let's talk about variance first, because after all, the name ANOVA indicates that it has something to do with variance.
What is the variance? It is the squared standard deviation and often written as s2 (for samples) or s2 (for population). The mathematical formula of variance (of population) is:
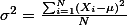 , where i indicates the ith number of individual; N indicates the total number of population;
, where i indicates the ith number of individual; N indicates the total number of population;  indicates the mean of the population.
indicates the mean of the population.So, basically what this formula says is that we compare each individual's score to the mean (m) of the population (to get the difference between the two), square the difference, keep doing this for all the individuals, sum the differences up, and divide the sum with the population size (N).
Why do we square the differences? Because unless we do that, the sum of the differences will be always zero. What does this variance mean? If you take a close look at the upper part and disregard the sigma sign, it is about how far an individual's score is from the mean of the population. In other words, how much each score varies from the mean of the population -- That's right, hence the name is the variance. We can also note that if each individuals vary a lot from the mean, the sum of the upper part will get bigger. This means a bigger variance indicates the individuals do not stick together around the mean. We can visualize this as follows.
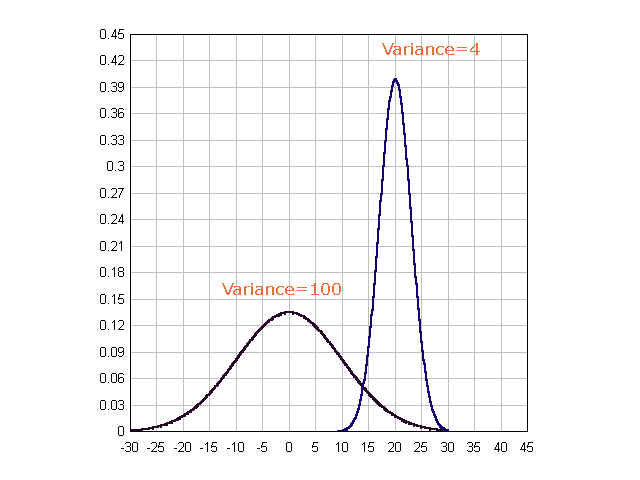
The first graph shows its variance is 100, which means its standard deviation is 10. The variance for the second is 4, hence, its standard deviation is 2. As we can see, the higher the variance value is, the wider the graph is (which means individuals vary a lot).

[JPG image (29.79 KB)]
The first graph shows its variance is 100, which means its standard deviation is 10. The variance for the second is 4, hence, its standard deviation is 2. As we can see, the higher the variance value is, the wider the graph is (which means individuals vary a lot).
note: This discussion can be also applied to the concept of standard deviation, which is squared root of the variance. When we talked about standard deviation, we also discussed the same characteristics.
The above formula is about population. When we talk about sample, the formula becomes slightly different -- but, not much.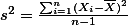 , where i indicates ith number of the individual, n indicates the number of the sample (that's right, a big N for population, small n for sample), x bar indicates the mean of the sample.
, where i indicates ith number of the individual, n indicates the number of the sample (that's right, a big N for population, small n for sample), x bar indicates the mean of the sample.note: This should remind you that we use Greek characters for representing population, English characters for representing sample. For example, m and s indicate the mean and the standard deviation of population, while x bar and s indicate the mean and the standard deviation of sample.
Using Greek letters or English letters may not seem important. But, the big difference between the above two formulae is N and n-1. Why do we use N for the population and why do we use n-1 for the sample? We can argue that if both are to get the same kind of things, called variance, regardless the difference between sample and population, we should use same number (N or N-1 for the population and n or n-1 for the sample)! The reason for using n-1 for sample is that size of a sample is smaller than that of population -- always, right?. Researchers and mathematicians have found that for small size, using n results in under-estimation of what they want to get. So, the variance obtained with one less from the number of the sample estimates the value of variance better.
see EstimatedStandardDeviation for more information.
Now take a look at the lower part of the formula, n-1. Have you seen this before? YES, YOU HAVE. Where? When we discussed t-test and chi-square test, we talked about the degrees of freedom. As far as I know (frankly I am not quite sure, if this is true), the n-1 is the degrees of freedom of a sample. So, the formula can be re-written as follows.
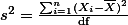 , where everything is the same, and df indicates degrees of freedom.
, where everything is the same, and df indicates degrees of freedom.We also call the upper part the Sum of Squared Differences and often use the abbreviation, SS. So, if we rewrite the formula again:
 , where SS is the Sum of Squared Differences , and df is the degrees of freedom .
, where SS is the Sum of Squared Differences , and df is the degrees of freedom .This so far was the discussion of variance. Again, you should be able to deduce the characteristics of variance from the formula, rather than memorizing the formula.
note: I know both -- deducing characteristics of variance and memorizing the formula are the same. But, sometimes, people try to memorize things without considering the rationale behind it. If this is the case of yours, you will quickly forget the formula right after an examination. If you know the meanings of variance, you will always draw the characteristics from the given formula. And by doing this, the chances are you will memorize and retain the formula without any difficulties.
Now, I guess we need to discuss the first part of ANOVA, ANalysis.
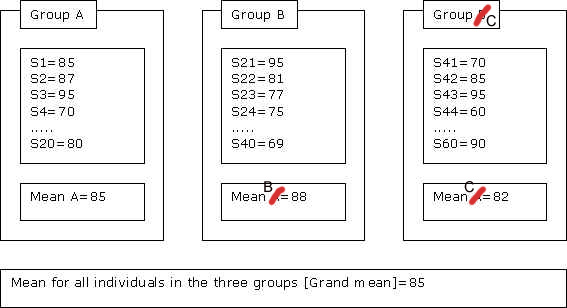
First, we need to discuss when we use ANOVA. Suppose we have three different groups -- say, group A is the students who use the class forum page as a study guide, group B is those who use review session as a study guide, and group C is those who just regularly attended the class. Then, suppose they had an exam and we got the exam result. With the information (exam result), we want to compare the three groups. That is, we can see if there is differences among the three groups. We can visualize this as follows.
[JPG image (38.15 KB)]
We can compare the three groups by examining the differences between individual scores to the total mean. But, there are two kinds of possible comparison. That is, first, I can compare the mean of each group (85, 88, 82 for Group A, B, C) to the grand mean (85). From this, we can see how far each group varies from the grand mean. Second, we can also compare how the scores of individuals in one group (s1, s2, s3, ... , s20 in Group A) vary from the mean of the group (Mean A=85). This will show how each individual varies from the mean of the group to which he or she belongs.
We can conceptualize this nicely with the terms that I have introduced earlier in this article. That is, the first part -- comparing mean of each group to the grand mean -- is actually comparing between group __(between group __analysis). The second part -- comparing each member with each others within a group -- is comparing within group (within group analysis).
And, by analysis, we mean we obtain the variances -- to see how scores vary from means -- of between groups and of within group. Let's name these two s2between (for between group) s2within (for within group). We can get the ratio between the s2between and s2within which is called F ratio:
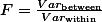
This is the basic about the ANOVA. Here we might have a question. That is, if we have three groups and are about to compare whether their exam scores differ from each other, why not use t-test? -- a valid question. With the t-test method, we can compare the group A and the group B; the group B and the group C; and the group C and the group A and see how one differs from each other.
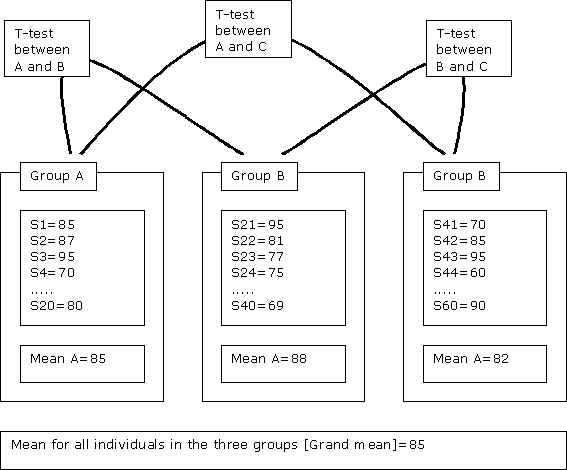
[JPG image (35.3 KB)]
It looks good and simple enough, doesn't it? The problem is when we do the t-test, we take a risk of being wrong -- usually 0.05 probability. When we compare A and B and state there is difference between the two, we take the risk of being false; and the risk is about 5 out of 100. Remember that this risk is the maximum tolerance we can take. In actual case, they (the comparison group) might be perfectly different, which indicates that there is no chance of lying about our conclusion. But, because we do not know about what the real situation is, when we do the statistics, we still assume that there is 5% risk. Or our assumption about being wrong may fully reflect the real situation. That is, the population indeed have some variation that every 5 cases out of 100 cases of sample examination turn out to be against our conclusion. (Remember here we still have 95 cases out of 100 total cases that show the conclusion is right -- after all this is what we admitted (about 95% confidence) in the first place by taking 0.05 probability risk).
Here, we have the same phenomenon (examination result) about one sample. If we partially do the t-test several times and if the reality really reflects our 0.05 probability risk, we actually accumulate the risk of being wrong. Of course, if the three groups are really different in reality and there is no chance of lying about this difference (remember here, the researchers, we, do not know this, we still take the 5% of chance while not knowing it is not necessary), it would be safe to use t-test several time toward the same phenomenon. But, again, we do not know this reality! What this indicates is that we cannot do the t-test several times toward one single phenomenon. It is like collecting beans in box with a small hole. While collecting and counting beans, we do not know how many we lost! Therefore, we turn to ANOVA and use it to see if there is any difference among the groups in exam performance.
So, the below is a graphic demonstration of the ANOVA test. We would like to see if the groups (as independent variable attributes) are different from one another. This means that the ideal type of being difference among the three groups should show (1) that there should be distinct difference among between groups and (2) there should be minimal differences among the individuals within the groups. The first one is easy to understand -- Each group should have distinctive, different mean score against other two. The second one shows that each group should have relatively small varieties within the group. In other words, the individual scores for each group should stick together around their group mean. This will represent that the individuals in the group are distinctively the same kinds and aggregation of such individuals will represent the distinctive difference against other groups. So, the below figure (figure 1) is a good example the three groups are really different. Each mean of the group doesn't share its mean score with others. Also individual scores stick together around the mean of their own groups.
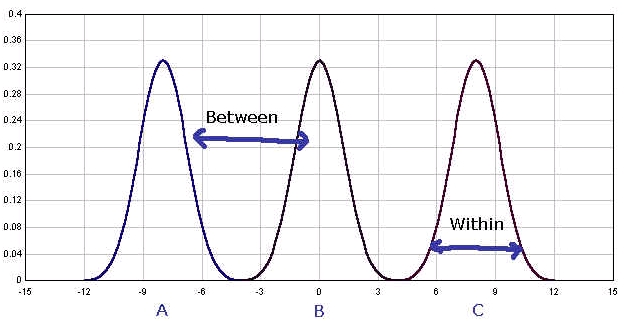
[JPG image (75.73 KB)]
Figure. 1
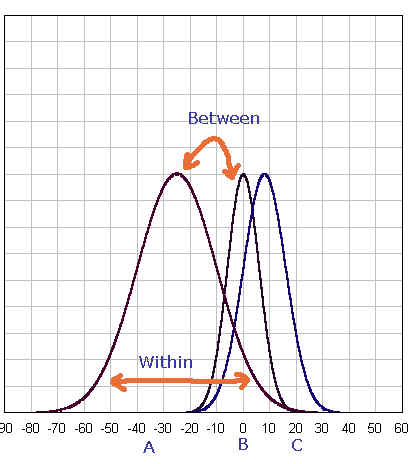
[JPG image (26.13 KB)]
Figure 2
On the other hand, figure 2 gives us a different story. Firs, it should be noted the shape of the curve differ from one another. The group A has the largest variance while group B has the smallest one (or standard deviation -- can you see why?). It should be also noted that if the bell-shape curves are wide (hence, large within variance), the mean difference between groups should be large. If the within variances are small (for the groups), even small amount of difference in mean scores will make the groups different from each other.
Let's go back to the F value, the ratio of the between variance and within variance. Take a look at the formula below.
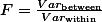
This shows the same thing we discussed the above. To summarize, we can think of this formula this way.
In the first place, we want to see if three groups are different in terms of exam score. In order to see a possible difference, the upper part (s2between) should be big; and the lower part (s2between) should be small. If this is the case, we can say that there is difference among the three groups in the exam scores.
And because F value is ratio of two variance values, the above 2, 3 are not fixed. That is, we can think of the relationship between the upper and lower part in this way, too. In the first place, we want to see if three groups are different in terms of exam score. In order to see a possible difference, the upper part (s2between) should be big; and the lower part (s2between) should be small. If this is the case, we can say that there is difference among the three groups in the exam scores.
If the lower part (s2within) is small enough or very small, even with a slight difference among the group (between variances among the three groups (s2between )), the F value will become large enough. In other words, if each group has small within-group variance, even slight difference of between-group variances will indicate that the three groups are distinctively different.
Anyway, you get the idea of ANOVA... Testing procedure is the same as the T-test. You obtain F-ratio value (as we did for T-test value or chi-square value), find out degrees of freedom (We have two. I did not discuss this for ANOVA. Please refer to the textbook); Read the F-test table (p. 300, in the textbook); pin down the critical value (with proper df). Compare them. If F-ratio is bigger than critical value, what should we do? -- You should be able to figure this out by this time.
12. External Links ¶
![[http]](/imgs/http.png) ANOVA one - way, M. Plonsky
ANOVA one - way, M. Plonsky![[http]](/imgs/http.png) ANOVA two - way, M. Plonsky
ANOVA two - way, M. Plonsky![[http]](/imgs/http.png) Concepts and Applications of Inferential Statistics - Dr. Richard Lowry
Concepts and Applications of Inferential Statistics - Dr. Richard Lowry