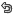아래의 예를 보면, 평균이 70이고 S=3인 normal distribution 그래프이다. 여기서 76 값은 Standard deviation 하나의 값만큼을 넘어서므로, 사선 밖에 위치한다. 그러나 다음 그림은 평균이 70; S=12인 그래프인데, 이경우에는 점수 76이 Standard deviation 하나의 값안에 존재하므로, 사선 안에 위치한다. 이 두 그래프를 모두 합치면 그림 3과 같다.
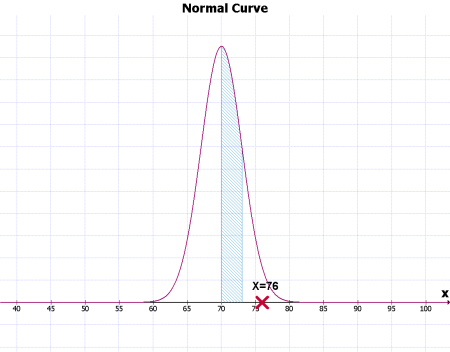
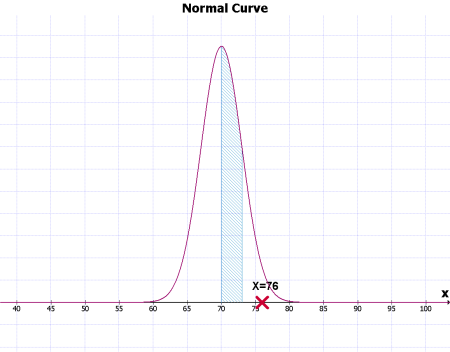
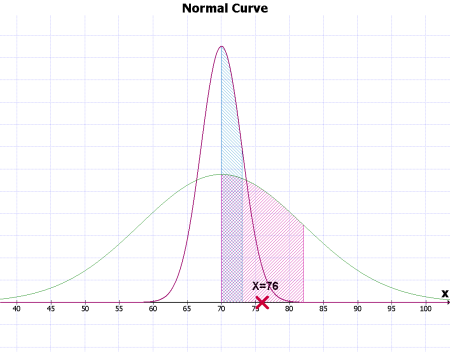

그림 1 [PNG image (36.39 KB)]

그림 2 [PNG image (36.39 KB)]

그림 3 [PNG image (51.56 KB)]
위에서 standard deviation 하나의 값이라고 표현한 것에 주목하자. 이렇게 부른 이유는 이 standard deviation 하나의 값을 하나의 unit으로 하고 싶어서다. 다시 말하면, 그림 1에서 점수 76은 하나의 unit밖에 존재한다. 사실, 이 그래프에서 76은 두개의 unit값만큼 떨어져 있다. 이렇게 normal distribution에서 standard deviation값을 unit화하여 단위로 나타내는 것을 standardization한다고 하고, 그 값을 z-score라고 한다 (z 에는 standardization의 의미가 있다).
그림 2의 그래프를 standard unit을 단위로하여 다시 그리면 아래와 같다.
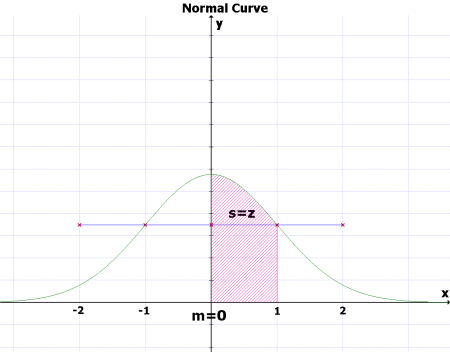
그림 3 [PNG image (29.33 KB)]
일반적으로 z-score는 아래와 같이 구해진다.

이와 같이 수식으로 생각을 하면,  을 평균값으로 하고
을 평균값으로 하고 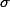 를 standard deviation값으로 하는 normal distribution곡선에서 나타나는 그 어떤 값이라도 수식에 대입해서 구할 수 있다. 즉,
를 standard deviation값으로 하는 normal distribution곡선에서 나타나는 그 어떤 값이라도 수식에 대입해서 구할 수 있다. 즉,
 을 평균값으로 하고
을 평균값으로 하고 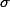 를 standard deviation값으로 하는 normal distribution곡선에서 나타나는 그 어떤 값이라도 수식에 대입해서 구할 수 있다. 즉,
를 standard deviation값으로 하는 normal distribution곡선에서 나타나는 그 어떤 값이라도 수식에 대입해서 구할 수 있다. 즉, 일때 점수 90의 z score는 아래와 같이 구해진다.
일때 점수 90의 z score는 아래와 같이 구해진다.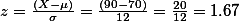
- 시험성적의 분포(distribution)가 평균(mean)=50 이고 standard deviation(sigma)은 8 이다. 이 때,
- 시험 점수 58의 z-score는?
b. 점수 46의 z-score?
c. z-score가 평균의 1/2 밑에 있을 때 시험 점수는?
- 시험 점수 58의 z-score는?
- 시험점수의 평균이 500 이고 STDev가 100 인 분포에서, 430 의 z-score는?

E.g.,
mean =60, stdev=12 의 distribution에서
mean =60, stdev=12 의 distribution에서
- z = +.25 일때의 raw score?
b. z = -1.2에서 raw score?
- Shape
- The mean
- The stdev
이에 대한 답은 각각의 점수가 다른 2개의 distribution에서 나왔기 때문에 비교할 수 없다는 것이다. 추가 정보가 없이는 갑돌이의 60점이 평균이상인지 이하인지도 알 길이 없다. 그렇다면, 이론 시험의 mean=50, sigma=10; 그리고 방법론 수업은 48, 4라고 가정을 하면, z-score 변환을 통해서 갑돌이의 점수를 평가할 수 있다.
이론 수업의 z-score는 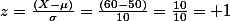
방법론의 z-score는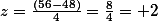
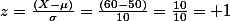
방법론의 z-score는
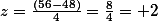
여기서 주목해야 할 것은 갑돌이의 방법론 수업이, 이론 수업의 점수보다 작지만, z-score로는 그 반대라는 점이다.
- Normal distribution, mean=50, stdev=8 의 분포를 z-score로 변환 하였을 때, 변환된 분포곡선의 mean, stdev은?