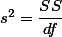Difference between r1.7 and the current
@@ -12,11 +12,11 @@
개인의 deviation score를 모두 더하는 것은 아래의 수식으로 표현할 수 있다. 즉, 어떤 집합의 개인의 숫자가 N이라고 하고, 각 개인을 X,,i,, 로 나타낼 때, deviation score의 합은 아래와 같다.
$Sum\; of\; Deviation \; Score = \sum_{i=1}^n ({X_i-\mu})$
$Sum\; of\; Deviation \; Score = \displaystyle \sum_{i=1}^n ({X_i-\mu})$
이를 집합을 이루는 개인의 숫자인 n으로 나누면 다음과 같이 표현할 수 있다.
$\text{Average \; of \; Deviation \; Score} = \frac{\sum_{i=1}^N {X_i-\mu}}{N}$
$\text{Average \; of \; Deviation \; Score} = \displaystyle \frac{\displaystyle \sum_{i=1}^N ({X_i-\mu})}{N}$
이렇게 하면 "개인들의 점수가 평균에서 얼마나 떨어져 있는지를 종합적으로 나타내 주는 지수가 될 수 있는것 처럼 보인다. '''그러나''', 이 방법의 문제는 deviation score의 합은 언제나 0이라는 점에 있다. 즉, 어떤 집합이든지 분산값을 위와 같이 구하려고 한다면, 그 분자 값은 언제나 0이 된다는 점이다. 사실 평균이 하는 역할 중의 하나는 바로 각 개인의 수치의 무게중심을 찾아 주는 역할이므로 이와 같은 결과가 당연하다. 아래는 이를 나타내 주는 예이다.
@@ -32,11 +32,11 @@
deviation score의 합을 구하기 전에 각 deviation score의 값을 제곱을 하여 주면 이와 같은 결과를 방지할 수 있는데, 이를 수식으로 표현하면 아래와 같다.
$\frac{\sum_{i=1}^N (X_i-\mu)^2}{N}$
$\displaystyle \frac{\displaystyle \sum_{i=1}^N (X_i-\mu)^2}{N}$
분산 값은 위와 같은 방법을 이용하여 구하게 된다. 따라서,
$Var[X] = \sigma^2= \frac{\sum_{i=1}^N (X_i-\mu)^2}{N}$
$Var[X] = \sigma^2= \displaystyle \frac{\displaystyle \sum_{i=1}^N (X_i-\mu)^2}{N}$
이를 우리나라 말로 옮기자면, "X 변인의 분산값은 X 변인의 각 개체값에서 평균값을 뺀 수의 제곱을 모두 더한 후, 이를 개체 수인 `n`으로 나누어 주어서 구한다"라고 읽는다. 따라서 위의 보기에서 들었던 X 변인의 집합에서 분산 값은 1.5이다.
@@ -52,18 +52,18 @@
분산의 공식을 5명으로 이루어진 집합에 사용하는 것은 큰 무리가 없지만, 100명으로 이루어진 집합에 적용하는 것은 손이 많이 간다는 단점이 있다. 따라서, 위의 분산 공식을 변형한 공식을 쓰기도 하는데, 형식만 다를 뿐이지 똑같은 공식이다.
$ \sigma^2 = \frac{\sum (X_i-\mu)^2}{N}$ 에서
$ \sigma^2 = \displaystyle \frac{\displaystyle \sum (X_i-\mu)^2}{N}$ 에서
{{{#!latex
\begin{eqnarray}
\begin{eqnarray*}
\sum (X_i-\mu)^2 & = & \sum [(X_i^2)-(2*X_i*\mu)+(\mu^2)] \\& = & \sum (X_i)^2 - \sum (2*X_i*\mu) + (\mu^2) \\
& = & \sum (X_i)^2 - \sum (2*X_i*\mu) + \sum (\mu^2) \\
& = & \sum (X_i)^2 - 2 \mu \sum (X_i) + N (\mu^2) \\& = & \sum (X_i)^2 - 2 \mu (N * \mu) + N (\mu^2) \\
& = & \sum (X_i^2) - N * \mu^2
\end{eqnarray}
\end{eqnarray*}
}}}x
위에서, $\text{2 and}$ $\mu$ $\text{are constants. }$@@ -79,8 +79,8 @@
{{{#!latex
\begin{eqnarray}
\sigma^2 & = \displaystyle \frac{\sum (X_i^2) - N * \mu^2}{N} \\
& = \displaystyle \frac{\sum (X_i^2)}{N} - \mu^2
\sigma^2 & = & \displaystyle \frac{\sum (X_i^2) - N * \mu^2}{N} \nonumber \\
& = & \displaystyle \frac{\sum (X_i^2)}{N} - \mu^2
\end{eqnarray}}}}
@@ -90,11 +90,11 @@
= Read more =샘플의 분산으로 모집단의 분산값을 추정할 때에는, 샘플의 숫자인 $n$ 대신에 $n-1$ 을 사용하기도 한다 (참조. [estimated standard deviation]. 샘플의 분산은 $s^2$ 을 기호로 사용한다.
$s^2 = Var[X] = \frac{\sum_{i=1}^n (X_i - \overline{X})^2}{n-1}$
$ s^2 = Var[X] = \displaystyle \frac{\displaystyle \sum_{i=1}^n (X_i - \overline{X})^2}{n-1}$
흔히들 부르기를, 분산 공식의 분자부분을 '''Sum of Squares'''라고 부르고 줄여서 '''SS'''라고 쓰고, n-1을 [degrees of freedom] 혹은 이를 줄여서 df라고 쓴다. 따라서 위의 분산을 구하는 식은 아래와 같이 표현될 수 있다.
$s^2 = \frac{SS}{df}$
$s^2 = \displaystyle \frac{SS}{df}$
See also [standard deviation] [wiki:StandardDeviation-eng]
----
Mean,Mode,Median 등의 중심경향값과 더불어서 많이 사용되는 statistics, 통계치로는 데이터가 얼마나 퍼져 있는지 (spread)를 나타내는 분산(variation)의 정도를 나타내 주는 statistics, 통계치가 있다. 가장 평이하고 이해하기 쉬운 개념으로는 범위 혹은 Range 가 있으며, 다소 직관적이지는 않지만 여러가지 통계 계산에 사용되는 것으로는 Variance(분산)이 있다.
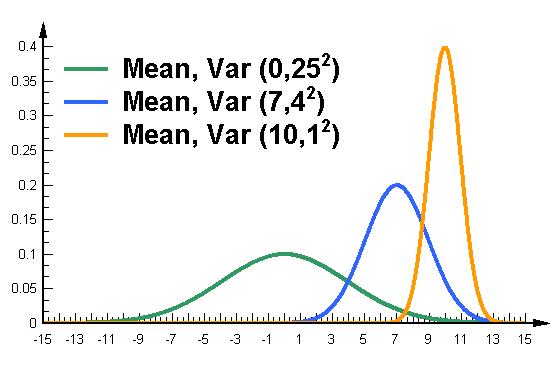
아래의 그래프는 각각 그 평균과 분산값이 다른 그래프이다. 각각 녹색라인의 경우 (가장 왼쪽), 평균은 0, 분산값은 25 이고; 청색라인은 평균이 7, 분산값은 4, 마지막으로 오렌지색 라인의 경우는 평균은 10, 분산 값은 1 인 경우이다 (please ignore the squre value in the figure).
[JPG image (27.92 KB)]
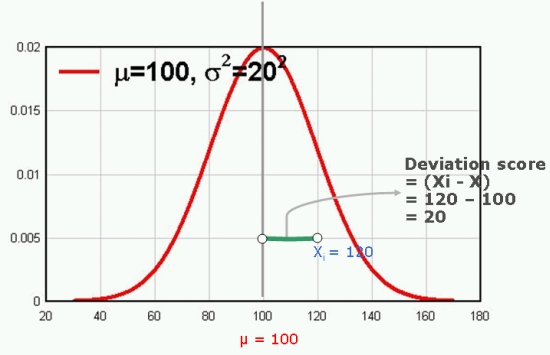
그림에서 직관적으로 보고 알 수 있듯이 분산은 그래프의 분포가 평균을 중심으로 얼마나 퍼져있는지를 (spread) 나타내주는 일종의 지표이다. 어떤 집합이 평균을 중심으로 얼마나 퍼져 있는가를 알아보기 위한 방법으로는 상식적으로 떠올릴 수 있는 것은 각 개인의 점수가 평균에서 얼마나 떨어져 있는가를 측정하여 모두 더한 후 이를 개인 수로 (number of elements) 나누는 방법을 떨올릴 수 있다. 개인의 점수가 평균에서 얼마나 떨어져 있는가를 deviation score라고 한다. 아래의 그래프는 평균이 100인 그래프를 그린 것인데, 어느 한 개인의 점수가 120이라고 하면 그 개인의 deviation score는 120-100, 즉 20이라고 할 수 있다.
[JPG image (57.43 KB)]
개인의 deviation score를 모두 더하는 것은 아래의 수식으로 표현할 수 있다. 즉, 어떤 집합의 개인의 숫자가 N이라고 하고, 각 개인을 Xi 로 나타낼 때, deviation score의 합은 아래와 같다.
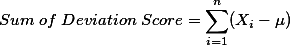
이를 집합을 이루는 개인의 숫자인 n으로 나누면 다음과 같이 표현할 수 있다.
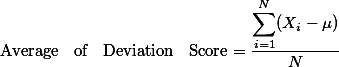
이렇게 하면 "개인들의 점수가 평균에서 얼마나 떨어져 있는지를 종합적으로 나타내 주는 지수가 될 수 있는것 처럼 보인다. 그러나, 이 방법의 문제는 deviation score의 합은 언제나 0이라는 점에 있다. 즉, 어떤 집합이든지 분산값을 위와 같이 구하려고 한다면, 그 분자 값은 언제나 0이 된다는 점이다. 사실 평균이 하는 역할 중의 하나는 바로 각 개인의 수치의 무게중심을 찾아 주는 역할이므로 이와 같은 결과가 당연하다. 아래는 이를 나타내 주는 예이다.
| X | score | deviation score |
| X1 | 3 | 3-4=-1 |
| X2 | 4 | 4-4=0 |
| X3 | 3 | 3-4=-1 |
| X4 | 4 | 4-4=0 |
| X5 | 6 | 6-4=2 |
| total | 20 | 0 |
| Mean | 4 | |
| n | 5 |
deviation score의 합을 구하기 전에 각 deviation score의 값을 제곱을 하여 주면 이와 같은 결과를 방지할 수 있는데, 이를 수식으로 표현하면 아래와 같다.
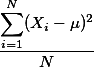
분산 값은 위와 같은 방법을 이용하여 구하게 된다. 따라서,
![$Var[X] = \sigma^2= \displaystyle \frac{\displaystyle \sum_{i=1}^N (X_i-\mu)^2}{N}$ $Var[X] = \sigma^2= \displaystyle \frac{\displaystyle \sum_{i=1}^N (X_i-\mu)^2}{N}$](/_cache/latex/1/14/1e18a8f78b9ecd63c691f280313b25ae.png)
이를 우리나라 말로 옮기자면, "X 변인의 분산값은 X 변인의 각 개체값에서 평균값을 뺀 수의 제곱을 모두 더한 후, 이를 개체 수인 n으로 나누어 주어서 구한다"라고 읽는다. 따라서 위의 보기에서 들었던 X 변인의 집합에서 분산 값은 1.5이다.
| X | score | deviation score | squared value |
| X1 | 3 | 3-4=-1 | 1 |
| X2 | 4 | 4-4=0 | 0 |
| X3 | 3 | 3-4=-1 | 1 |
| X4 | 4 | 4-4=0 | 0 |
| X5 | 6 | 6-4=2 | 4 |
| total | 20 | 0 | 6 |
| Mean, Variance | 4 | 6/4 = 1.5 | |
| n | 5 | 5 |
분산의 공식을 5명으로 이루어진 집합에 사용하는 것은 큰 무리가 없지만, 100명으로 이루어진 집합에 적용하는 것은 손이 많이 간다는 단점이 있다. 따라서, 위의 분산 공식을 변형한 공식을 쓰기도 하는데, 형식만 다를 뿐이지 똑같은 공식이다.
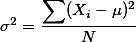 에서
에서![\begin{eqnarray*}
\sum (X_i-\mu)^2 & = & \sum [(X_i^2)-(2*X_i*\mu)+(\mu^2)] \\
& = & \sum (X_i)^2 - \sum (2*X_i*\mu) + \sum (\mu^2) \\
& = & \sum (X_i)^2 - 2 \mu \sum (X_i) + N (\mu^2) \\
& = & \sum (X_i)^2 - 2 \mu (N * \mu) + N (\mu^2) \\
& = & \sum (X_i^2) - N * \mu^2
\end{eqnarray*}
\begin{eqnarray*}
\sum (X_i-\mu)^2 & = & \sum [(X_i^2)-(2*X_i*\mu)+(\mu^2)] \\
& = & \sum (X_i)^2 - \sum (2*X_i*\mu) + \sum (\mu^2) \\
& = & \sum (X_i)^2 - 2 \mu \sum (X_i) + N (\mu^2) \\
& = & \sum (X_i)^2 - 2 \mu (N * \mu) + N (\mu^2) \\
& = & \sum (X_i^2) - N * \mu^2
\end{eqnarray*}](/_cache/latex/e/e7/611e7a4d744ba847af269ab822b9809d.png)
x
위에서,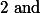

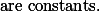
위에서,
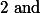

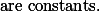
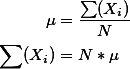
따라서 분산값은 아래의 공식으로도 구할 수 있다.
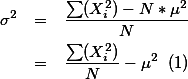
분산값이 크고 작고가 의미하는 것은 그 집합의 분포가 평균을 중심으로 얼마나 넓게 퍼져 있는가를 나타내 준다는 것이다. 만약에 분산 값이 크다면 그 집합의 분포가 평균을 중심으로 넓게 퍼져있음을 의미한다.
Read more ¶
샘플의 분산으로 모집단의 분산값을 추정할 때에는, 샘플의 숫자인 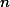 대신에
대신에  을 사용하기도 한다 (참조. estimated standard deviation. 샘플의 분산은
을 사용하기도 한다 (참조. estimated standard deviation. 샘플의 분산은 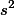 을 기호로 사용한다.
을 기호로 사용한다.
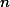 대신에
대신에  을 사용하기도 한다 (참조. estimated standard deviation. 샘플의 분산은
을 사용하기도 한다 (참조. estimated standard deviation. 샘플의 분산은 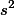 을 기호로 사용한다.
을 기호로 사용한다. ![$ s^2 = Var[X] = \displaystyle \frac{\displaystyle \sum_{i=1}^n (X_i - \overline{X})^2}{n-1}$ $ s^2 = Var[X] = \displaystyle \frac{\displaystyle \sum_{i=1}^n (X_i - \overline{X})^2}{n-1}$](/_cache/latex/a/a5/319edf8c5e731a92dfffd1ecb8b176d4.png)
흔히들 부르기를, 분산 공식의 분자부분을 Sum of Squares라고 부르고 줄여서 SS라고 쓰고, n-1을 degrees of freedom 혹은 이를 줄여서 df라고 쓴다. 따라서 위의 분산을 구하는 식은 아래와 같이 표현될 수 있다.